 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Einführung in neuronale Netze, die auf physikalischen Informationen basieren
Einführung in neuronale Netze, die auf physikalischen Informationen basieren
Einführung in neuronale Netze, die auf physikalischen Informationen basieren

Physically Information Based Neural Network (PINN) ist eine Methode, die physikalische Modelle und neuronale Netze kombiniert. Durch die Integration physikalischer Methoden in neuronale Netze kann PINN das dynamische Verhalten nichtlinearer Systeme lernen. Im Vergleich zu herkömmlichen physikalischen modellbasierten Methoden weist PINN eine höhere Flexibilität und Skalierbarkeit auf. Es kann komplexe nichtlineare dynamische Systeme adaptiv erlernen und gleichzeitig die Anforderungen physikalischer Spezifikationen erfüllen. In diesem Artikel werden die Grundprinzipien von PINN vorgestellt und einige praktische Anwendungsbeispiele bereitgestellt.
Das Grundprinzip von PINN besteht darin, physikalische Methoden in neuronale Netze zu integrieren, um das dynamische Verhalten des Systems zu lernen. Konkret können wir die physikalische Methode wie folgt ausdrücken:
F(u(x),frac{partial u}{partial x},x,t)=0
Unser Ziel ist es, Learn zu bestehen die zeitliche Entwicklung der Systemzustandsänderung u(x) und die Randbedingungen rund um das System, um ein Verständnis des Systemverhaltens zu erlangen. Um dieses Ziel zu erreichen, können wir mithilfe eines neuronalen Netzwerks die Entwicklung der Zustandsänderung u(x) simulieren und mithilfe automatischer Differenzierungstechniken den Gradienten der Zustandsänderung berechnen. Gleichzeitig können wir auch physikalische Methoden nutzen, um die Beziehung zwischen neuronalen Netzen und Zustandsänderungen einzuschränken. Auf diese Weise können wir die Zustandsentwicklung des Systems besser verstehen und zukünftige Änderungen vorhersagen.
Konkret können wir die folgende Verlustfunktion verwenden, um PINN zu trainieren:
L_{pinn}=L_{Daten}+L_{Physik}
wobei L_{Daten} der verwendete Datenverlust ist zur Simulation bekannter Zustandsänderungswerte. Im Allgemeinen können wir den mittleren quadratischen Fehler verwenden, um L_{data} definitiv zu definieren:
L_{data}=frac{1}{N}sum_{i=1}^{N}(u_i-u_{data, i })^2
wobei $N$ die Anzahl der Stichproben im Datensatz ist, u_i der vom neuronalen Netzwerk vorhergesagte Zustandsänderungswert ist und u_{data,i} der entsprechende reale Zustandsänderungswert in ist Der Datensatz.
L_{Physik} ist der physikalische Einschränkungsverlust, der verwendet wird, um sicherzustellen, dass das neuronale Netzwerk und Zustandsänderungen die physikalische Methode erfüllen. Im Allgemeinen können wir die Anzahl der Residuen verwenden, um L_{Physik} definitiv zu definieren:
L_{Physik}=frac{1}{N}sum_{i=1}^{N}(F(u_i,frac{ partielles u_i}{partielles x},x_i,t_i))^2
wobei F die physikalische Methode ist, frac{partielles u_i}{partielles x} die Steigung der vom neuronalen Netzwerk vorhergesagten Zustandsänderung ist, x_i und t_i ähnelt diesem Die Raum- und Zeitkoordinaten von i.
Durch die Minimierung von L_{pinn} können wir gleichzeitig Daten simulieren und physikalische Methoden erfüllen und so das dynamische Verhalten des Systems lernen.
Schauen wir uns nun einige realistische PINN-Demonstrationen an. Ein typisches Beispiel ist das Erlernen des dynamischen Verhaltens der Navier-Stokes-Methode. Die Navier-Stokes-Methode beschreibt das Bewegungsverhalten der Flüssigkeit, das in der folgenden Form geschrieben werden kann:
rho(frac{partial u}{partial t}+ucdotnabla u)=-nabla p+munabla^2u+ f
Wobei rho die Dichte der Flüssigkeit ist, u die Geschwindigkeit der Flüssigkeit ist, p der Druck der Flüssigkeit ist, mu die Dichte der Flüssigkeit ist und f die äußere Kraft ist. Unser Ziel ist es, die zeitliche Entwicklung der Geschwindigkeit und des Drucks der Flüssigkeit sowie die Randbedingungen an der Flüssigkeitsgrenze zu erfahren.
Um dieses Ziel zu erreichen, können wir die Navier-Stokes-Methode in das neuronale Netzwerk integrieren, um die Lerngeschwindigkeit und die zeitliche Druckentwicklung zu erleichtern. Konkret können wir den folgenden Verlust verwenden, um PINN zu trainieren:
L_{pinn}=L_{data}+L_{physics}
wobei die Definitionen von L_{data} und L_{physics} dieselben wie zuvor sind . Wir können ein Fluiddynamikmodell verwenden, um einen Satz Zustandsvariablendaten einschließlich Geschwindigkeit und Druck zu generieren, und dann PINN verwenden, um Zustandsänderungen zu simulieren und die Navier-Stokes-Methode zu erfüllen. Auf diese Weise können wir das dynamische Verhalten strömender Körper, einschließlich Phänomene wie Nassströmungen, Wirbel und Grenzschichten, lernen, ohne zunächst ein komplexes physikalisches Modell ermitteln oder die Analyse manuell ableiten zu müssen.
Ein weiteres Beispiel ist das Erlernen des kinematischen Verhaltens nichtlinearer Wellenbewegungsmethoden. Die nichtlineare Wellenbewegungsmethode beschreibt in der Einleitung das Ausbreitungsverhalten der Wellenbewegung, das in der folgenden Form geschrieben werden kann:
frac{partial^2u}{partial t^2}-c^2nabla^2u+f( u) =0
wobei u die Amplitude der Wellengeschwindigkeit ist, c die Wellengeschwindigkeit ist und f(u) das Element nichtlinearer Qualität ist. Unser Ziel ist es, die zeitliche Entwicklung der Wellendynamik und Randbedingungen an den Einführungsgrenzen zu erfahren.
Um dieses Ziel zu erreichen, können wir nichtlineare Wellenprozesse in neuronale Netze integrieren, um das Lernen der epochalen Entwicklung der Wellenbewegung zu erleichtern. Konkret können wir die folgenden Schadenszahlen verwenden, um PINN zu trainieren:
L_{pinn}=L_{data}+L_{physics}
wobei L_{data} und L_{physics} als „Gleich wie“ definiert sind über. Wir können numerische Methoden verwenden, um einen Satz von Zustandsänderungsdaten zu generieren, die Amplituden und Schritte enthalten, und dann PINN verwenden, um die Zustandsänderungen zu simulieren und die nichtlineare Wellenmethode zu erfüllen. Auf diese Weise können wir die zeitliche Entwicklung von Wellen in einem Medium untersuchen, einschließlich Phänomenen wie Formänderungen, Brechung und Reflexion von Wellenpaketen, ohne zunächst komplexe physikalische Modelle zu definieren oder die Analyse manuell abzuleiten.
Kurz gesagt ist das auf physikalischen Informationen basierende neuronale Netzwerk eine Methode, die physikalische Modelle und neuronale Netzwerke kombiniert, die sich an das Lernen komplexer nichtlinearer dynamischer Systeme auf der Erde anpassen und gleichzeitig die physikalischen Gesetze strikt erfüllen können. PINN wird in der Strömungsmechanik, Akustik, Strukturmechanik und anderen Bereichen häufig eingesetzt und hat einige bemerkenswerte Ergebnisse erzielt. Mit der kontinuierlichen Weiterentwicklung neuronaler Netze und automatisierter Differentialtechnologie wird PINN in Zukunft hoffentlich zu einem größeren, stärkeren und vielseitigeren Werkzeug zur Lösung verschiedener nichtlinearer Dynamikprobleme werden.
Das obige ist der detaillierte Inhalt vonEinführung in neuronale Netze, die auf physikalischen Informationen basieren. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 Entdecken Sie die Konzepte, Unterschiede, Vor- und Nachteile von RNN, LSTM und GRU
Jan 22, 2024 pm 07:51 PM
Entdecken Sie die Konzepte, Unterschiede, Vor- und Nachteile von RNN, LSTM und GRU
Jan 22, 2024 pm 07:51 PM
In Zeitreihendaten gibt es Abhängigkeiten zwischen Beobachtungen, sie sind also nicht unabhängig voneinander. Herkömmliche neuronale Netze behandeln jedoch jede Beobachtung als unabhängig, was die Fähigkeit des Modells zur Modellierung von Zeitreihendaten einschränkt. Um dieses Problem zu lösen, wurde das Recurrent Neural Network (RNN) eingeführt, das das Konzept des Speichers einführte, um die dynamischen Eigenschaften von Zeitreihendaten zu erfassen, indem Abhängigkeiten zwischen Datenpunkten im Netzwerk hergestellt werden. Durch wiederkehrende Verbindungen kann RNN frühere Informationen an die aktuelle Beobachtung weitergeben, um zukünftige Werte besser vorherzusagen. Dies macht RNN zu einem leistungsstarken Werkzeug für Aufgaben mit Zeitreihendaten. Aber wie erreicht RNN diese Art von Gedächtnis? RNN realisiert das Gedächtnis durch die Rückkopplungsschleife im neuronalen Netzwerk. Dies ist der Unterschied zwischen RNN und herkömmlichen neuronalen Netzwerken.
 Berechnung von Gleitkommaoperanden (FLOPS) für neuronale Netze
Jan 22, 2024 pm 07:21 PM
Berechnung von Gleitkommaoperanden (FLOPS) für neuronale Netze
Jan 22, 2024 pm 07:21 PM
FLOPS ist einer der Standards zur Bewertung der Computerleistung und dient zur Messung der Anzahl der Gleitkommaoperationen pro Sekunde. In neuronalen Netzen wird FLOPS häufig verwendet, um die Rechenkomplexität des Modells und die Nutzung von Rechenressourcen zu bewerten. Es ist ein wichtiger Indikator zur Messung der Rechenleistung und Effizienz eines Computers. Ein neuronales Netzwerk ist ein komplexes Modell, das aus mehreren Neuronenschichten besteht und für Aufgaben wie Datenklassifizierung, Regression und Clustering verwendet wird. Das Training und die Inferenz neuronaler Netze erfordert eine große Anzahl von Matrixmultiplikationen, Faltungen und anderen Rechenoperationen, sodass die Rechenkomplexität sehr hoch ist. Mit FLOPS (FloatingPointOperationsperSecond) kann die Rechenkomplexität neuronaler Netze gemessen werden, um die Effizienz der Rechenressourcennutzung des Modells zu bewerten. FLOP
 Eine Fallstudie zur Verwendung des bidirektionalen LSTM-Modells zur Textklassifizierung
Jan 24, 2024 am 10:36 AM
Eine Fallstudie zur Verwendung des bidirektionalen LSTM-Modells zur Textklassifizierung
Jan 24, 2024 am 10:36 AM
Das bidirektionale LSTM-Modell ist ein neuronales Netzwerk, das zur Textklassifizierung verwendet wird. Unten finden Sie ein einfaches Beispiel, das zeigt, wie bidirektionales LSTM für Textklassifizierungsaufgaben verwendet wird. Zuerst müssen wir die erforderlichen Bibliotheken und Module importieren: importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 Definition und Strukturanalyse eines Fuzzy-Neuronalen Netzwerks
Jan 22, 2024 pm 09:09 PM
Definition und Strukturanalyse eines Fuzzy-Neuronalen Netzwerks
Jan 22, 2024 pm 09:09 PM
Das Fuzzy-Neuronale Netzwerk ist ein Hybridmodell, das Fuzzy-Logik und neuronale Netzwerke kombiniert, um unscharfe oder unsichere Probleme zu lösen, die mit herkömmlichen neuronalen Netzwerken nur schwer zu bewältigen sind. Sein Design ist von der Unschärfe und Unsicherheit der menschlichen Wahrnehmung inspiriert und wird daher häufig in Steuerungssystemen, Mustererkennung, Data Mining und anderen Bereichen eingesetzt. Die Grundarchitektur eines Fuzzy-Neuronalen Netzwerks besteht aus einem Fuzzy-Subsystem und einem Neuronalen Subsystem. Das Fuzzy-Subsystem verwendet Fuzzy-Logik, um Eingabedaten zu verarbeiten und in Fuzzy-Sätze umzuwandeln, um die Unschärfe und Unsicherheit der Eingabedaten auszudrücken. Das neuronale Subsystem nutzt neuronale Netze zur Verarbeitung von Fuzzy-Sets für Aufgaben wie Klassifizierung, Regression oder Clustering. Durch die Interaktion zwischen dem Fuzzy-Subsystem und dem neuronalen Subsystem verfügt das Fuzzy-Neuronale Netzwerk über leistungsfähigere Verarbeitungsfähigkeiten und kann
 Einführung in SqueezeNet und seine Eigenschaften
Jan 22, 2024 pm 07:15 PM
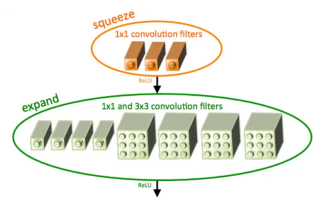
Einführung in SqueezeNet und seine Eigenschaften
Jan 22, 2024 pm 07:15 PM
SqueezeNet ist ein kleiner und präziser Algorithmus, der eine gute Balance zwischen hoher Genauigkeit und geringer Komplexität schafft und sich daher ideal für mobile und eingebettete Systeme mit begrenzten Ressourcen eignet. Im Jahr 2016 schlugen Forscher von DeepScale, der University of California, Berkeley und der Stanford University SqueezeNet vor, ein kompaktes und effizientes Faltungs-Neuronales Netzwerk (CNN). In den letzten Jahren haben Forscher mehrere Verbesserungen an SqueezeNet vorgenommen, darunter SqueezeNetv1.1 und SqueezeNetv2.0. Verbesserungen in beiden Versionen erhöhen nicht nur die Genauigkeit, sondern senken auch die Rechenkosten. Genauigkeit von SqueezeNetv1.1 im ImageNet-Datensatz
 Bildrauschen mithilfe von Faltungs-Neuronalen Netzen
Jan 23, 2024 pm 11:48 PM
Bildrauschen mithilfe von Faltungs-Neuronalen Netzen
Jan 23, 2024 pm 11:48 PM
Faltungs-Neuronale Netze eignen sich gut für Aufgaben zur Bildrauschunterdrückung. Es nutzt die erlernten Filter, um das Rauschen zu filtern und so das Originalbild wiederherzustellen. In diesem Artikel wird die Methode zur Bildentrauschung basierend auf einem Faltungs-Neuronalen Netzwerk ausführlich vorgestellt. 1. Überblick über das Convolutional Neural Network Das Convolutional Neural Network ist ein Deep-Learning-Algorithmus, der eine Kombination aus mehreren Faltungsschichten, Pooling-Schichten und vollständig verbundenen Schichten verwendet, um Bildmerkmale zu lernen und zu klassifizieren. In der Faltungsschicht werden die lokalen Merkmale des Bildes durch Faltungsoperationen extrahiert und so die räumliche Korrelation im Bild erfasst. Die Pooling-Schicht reduziert den Rechenaufwand durch Reduzierung der Feature-Dimension und behält die Hauptfeatures bei. Die vollständig verbundene Schicht ist für die Zuordnung erlernter Merkmale und Beschriftungen zur Implementierung der Bildklassifizierung oder anderer Aufgaben verantwortlich. Das Design dieser Netzwerkstruktur macht das Faltungs-Neuronale Netzwerk für die Bildverarbeitung und -erkennung nützlich.
 Schritte zum Schreiben eines einfachen neuronalen Netzwerks mit Rust
Jan 23, 2024 am 10:45 AM
Schritte zum Schreiben eines einfachen neuronalen Netzwerks mit Rust
Jan 23, 2024 am 10:45 AM
Rust ist eine Programmiersprache auf Systemebene, die sich auf Sicherheit, Leistung und Parallelität konzentriert. Ziel ist es, eine sichere und zuverlässige Programmiersprache bereitzustellen, die für Szenarien wie Betriebssysteme, Netzwerkanwendungen und eingebettete Systeme geeignet ist. Die Sicherheit von Rust beruht hauptsächlich auf zwei Aspekten: dem Eigentumssystem und dem Kreditprüfer. Das Besitzsystem ermöglicht es dem Compiler, den Code zur Kompilierungszeit auf Speicherfehler zu überprüfen und so häufige Speichersicherheitsprobleme zu vermeiden. Indem Rust die Überprüfung der Eigentumsübertragungen von Variablen zur Kompilierungszeit erzwingt, stellt Rust sicher, dass Speicherressourcen ordnungsgemäß verwaltet und freigegeben werden. Der Borrow-Checker analysiert den Lebenszyklus der Variablen, um sicherzustellen, dass nicht mehrere Threads gleichzeitig auf dieselbe Variable zugreifen, wodurch häufige Sicherheitsprobleme bei der Parallelität vermieden werden. Durch die Kombination dieser beiden Mechanismen ist Rust in der Lage, Folgendes bereitzustellen
 Twin Neural Network: Prinzip- und Anwendungsanalyse
Jan 24, 2024 pm 04:18 PM
Twin Neural Network: Prinzip- und Anwendungsanalyse
Jan 24, 2024 pm 04:18 PM
Das Siamese Neural Network ist eine einzigartige künstliche neuronale Netzwerkstruktur. Es besteht aus zwei identischen neuronalen Netzen mit denselben Parametern und Gewichten. Gleichzeitig teilen die beiden Netzwerke auch die gleichen Eingabedaten. Dieses Design wurde von Zwillingen inspiriert, da die beiden neuronalen Netze strukturell identisch sind. Das Prinzip des siamesischen neuronalen Netzwerks besteht darin, bestimmte Aufgaben wie Bildabgleich, Textabgleich und Gesichtserkennung durch den Vergleich der Ähnlichkeit oder des Abstands zwischen zwei Eingabedaten auszuführen. Während des Trainings versucht das Netzwerk, ähnliche Daten benachbarten Regionen und unterschiedliche Daten entfernten Regionen zuzuordnen. Auf diese Weise kann das Netzwerk lernen, verschiedene Daten zu klassifizieren oder abzugleichen, um entsprechende Ergebnisse zu erzielen



