 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Anwendung der Sigmoidfunktion in künstlichen neuronalen Netzwerken
Anwendung der Sigmoidfunktion in künstlichen neuronalen Netzwerken
Anwendung der Sigmoidfunktion in künstlichen neuronalen Netzwerken

In künstlichen neuronalen Netzen wird die Sigmoidfunktion häufig als Aktivierungsfunktion von Neuronen verwendet, um nichtlineare Eigenschaften einzuführen. Dadurch können neuronale Netze komplexere Entscheidungsgrenzen erlernen und eine wichtige Rolle in verschiedenen Anwendungen wie Bilderkennung, Verarbeitung natürlicher Sprache und Spracherkennung spielen.
Die Sigmoidfunktion ist eine häufig verwendete mathematische Funktion, die jeden Eingabewert einem Wert zwischen 0 und 1 zuordnen kann. Daher wird sie häufig bei binären Klassifizierungs- und logistischen Regressionsproblemen verwendet. Diese Funktion zeichnet sich durch eine „S“-Form aus, die zunächst langsam ansteigt, sich dann schnell dem Wert 1 nähert und sich schließlich einpendelt.
Die Sigmoidfunktion verstehen
Die Sigmoidfunktion ist eine häufig verwendete mathematische Funktion, mit der Eingabewerte dem Bereich zwischen 0 und 1 zugeordnet werden. Seine mathematische Definition ist 1/(1+e^(-x)), wobei x der Eingabewert und e die Konstante 2,718 ist. Diese Funktion ist bei binären Klassifizierungs- und logistischen Regressionsproblemen sehr nützlich. Sein Wertebereich ist (0,1) und seine Domäne ist (-unendlich, +unendlich). Das Merkmal der S-förmigen Funktion besteht darin, dass sie jede reale Eingabe in einen Wahrscheinlichkeitswert umwandeln kann. Daher wird sie häufig in der Ausgabeschicht des Modells beim maschinellen Lernen und in der Statistik verwendet.
Eine der Schlüsseleigenschaften der Sigmoidfunktion besteht darin, dass ihr Ausgabewert mit zunehmendem Eingabewert eine „S“-förmige Kurve aufweist. Wenn der Eingabewert steigt, erhöht sich der Ausgabewert allmählich und nähert sich schließlich 1. Diese Funktion bietet wichtige Funktionen für die Modellierung von Entscheidungsgrenzen bei binären Klassifizierungsproblemen.
Eine weitere wichtige Eigenschaft der Sigmoidfunktion ist ihre Ableitung, die eine Schlüsselrolle beim Training neuronaler Netzwerke spielt. Die Ableitung der Sigmoidfunktion ist als f(x)(1-f(x)) definiert, wobei f(x) die Ausgabe der Funktion darstellt. Die Existenz von Derivaten ermöglicht es dem neuronalen Netzwerk, die Gewichte und Bias von Neuronen effektiver anzupassen und dadurch die Leistung des Netzwerks zu verbessern. Durch die Berechnung von Ableitungen kann das Netzwerk Parameter basierend auf dem Gradienten der Verlustfunktion aktualisieren, sodass das Netzwerk die Genauigkeit schrittweise optimieren und verbessern kann. Diese Methode, Ableitungen zum Trainieren von Netzwerken zu verwenden, wird häufig im Bereich Deep Learning eingesetzt und ermöglicht es neuronalen Netzwerken, zu lernen und sich an eine Vielzahl komplexer Aufgaben anzupassen.
Zusätzlich zur Sigmoidfunktion gibt es weitere Aktivierungsfunktionen wie ReLU und Tanh, die die Einschränkungen der Sigmoidfunktion ausgleichen können. Die Ausgabe der Sigmoidfunktion liegt immer zwischen 0 und 1, was zu Problemen führen kann, wenn die Ausgabe des Netzwerks größer als 1 oder kleiner als 0 sein muss. Die ReLU-Funktion kann dieses Problem lösen, indem sie negative Zahlen auf 0 abbildet, während positive Zahlen unverändert bleiben. Darüber hinaus ist die Tanh-Funktion auch eine häufig verwendete Aktivierungsfunktion. Ihr Ausgabebereich liegt zwischen -1 und 1, was flexibler ist als die Sigmoidfunktion. Daher können beim Entwurf eines neuronalen Netzwerks je nach Bedarf unterschiedliche Aktivierungsfunktionen ausgewählt werden, um bessere Ergebnisse zu erzielen.
Die Visualisierung der Sigmoidfunktion mithilfe von Diagrammen hilft, ihre Eigenschaften besser zu verstehen. Das Diagramm zeigt die „S“-Form der Funktion und wie sich der Ausgabewert ändert, wenn sich der Eingabewert ändert.
Sigmoidfunktion in künstlichen neuronalen Netzen
Die Sigmoidfunktion wird üblicherweise als Aktivierungsfunktion künstlicher neuronaler Netze verwendet. In einem vorwärtsgerichteten neuronalen Netzwerk wird die Ausgabe jedes Neurons durch eine Sigmoidfunktion verarbeitet, die nichtlineare Eigenschaften in das Modell einführen kann. Die Einführung nichtlinearer Eigenschaften ist wichtig, da sie es dem neuronalen Netzwerk ermöglicht, komplexere Entscheidungsgrenzen zu lernen und dadurch seine Leistung bei bestimmten Aufgaben zu verbessern.
Vorteile:
- Erzeugt Ausgabewerte zwischen 0 und 1, was bei binären Klassifizierungs- und logistischen Regressionsproblemen hilfreich ist.
- Differenzierbar bedeutet, dass seine Ableitungen berechnet werden können und es einfach ist, das Netzwerk durch Anpassen der Gewichte und Vorspannungen von Neuronen zu optimieren.
Nachteile:
- Es können Ausgabewerte nahe 0 oder 1 erzeugt werden, was zu Problemen mit dem Optimierungsalgorithmus führen kann.
- Der Gradient der Sigmoidfunktion wird in der Nähe des Ausgabewerts 0 oder 1 sehr klein, was es für den Optimierungsalgorithmus schwierig macht, die Gewichte und Bias der Neuronen anzupassen.
Das obige ist der detaillierte Inhalt vonAnwendung der Sigmoidfunktion in künstlichen neuronalen Netzwerken. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 Entdecken Sie die Konzepte, Unterschiede, Vor- und Nachteile von RNN, LSTM und GRU
Jan 22, 2024 pm 07:51 PM
Entdecken Sie die Konzepte, Unterschiede, Vor- und Nachteile von RNN, LSTM und GRU
Jan 22, 2024 pm 07:51 PM
In Zeitreihendaten gibt es Abhängigkeiten zwischen Beobachtungen, sie sind also nicht unabhängig voneinander. Herkömmliche neuronale Netze behandeln jedoch jede Beobachtung als unabhängig, was die Fähigkeit des Modells zur Modellierung von Zeitreihendaten einschränkt. Um dieses Problem zu lösen, wurde das Recurrent Neural Network (RNN) eingeführt, das das Konzept des Speichers einführte, um die dynamischen Eigenschaften von Zeitreihendaten zu erfassen, indem Abhängigkeiten zwischen Datenpunkten im Netzwerk hergestellt werden. Durch wiederkehrende Verbindungen kann RNN frühere Informationen an die aktuelle Beobachtung weitergeben, um zukünftige Werte besser vorherzusagen. Dies macht RNN zu einem leistungsstarken Werkzeug für Aufgaben mit Zeitreihendaten. Aber wie erreicht RNN diese Art von Gedächtnis? RNN realisiert das Gedächtnis durch die Rückkopplungsschleife im neuronalen Netzwerk. Dies ist der Unterschied zwischen RNN und herkömmlichen neuronalen Netzwerken.
 Berechnung von Gleitkommaoperanden (FLOPS) für neuronale Netze
Jan 22, 2024 pm 07:21 PM
Berechnung von Gleitkommaoperanden (FLOPS) für neuronale Netze
Jan 22, 2024 pm 07:21 PM
FLOPS ist einer der Standards zur Bewertung der Computerleistung und dient zur Messung der Anzahl der Gleitkommaoperationen pro Sekunde. In neuronalen Netzen wird FLOPS häufig verwendet, um die Rechenkomplexität des Modells und die Nutzung von Rechenressourcen zu bewerten. Es ist ein wichtiger Indikator zur Messung der Rechenleistung und Effizienz eines Computers. Ein neuronales Netzwerk ist ein komplexes Modell, das aus mehreren Neuronenschichten besteht und für Aufgaben wie Datenklassifizierung, Regression und Clustering verwendet wird. Das Training und die Inferenz neuronaler Netze erfordert eine große Anzahl von Matrixmultiplikationen, Faltungen und anderen Rechenoperationen, sodass die Rechenkomplexität sehr hoch ist. Mit FLOPS (FloatingPointOperationsperSecond) kann die Rechenkomplexität neuronaler Netze gemessen werden, um die Effizienz der Rechenressourcennutzung des Modells zu bewerten. FLOP
 Eine Fallstudie zur Verwendung des bidirektionalen LSTM-Modells zur Textklassifizierung
Jan 24, 2024 am 10:36 AM
Eine Fallstudie zur Verwendung des bidirektionalen LSTM-Modells zur Textklassifizierung
Jan 24, 2024 am 10:36 AM
Das bidirektionale LSTM-Modell ist ein neuronales Netzwerk, das zur Textklassifizierung verwendet wird. Unten finden Sie ein einfaches Beispiel, das zeigt, wie bidirektionales LSTM für Textklassifizierungsaufgaben verwendet wird. Zuerst müssen wir die erforderlichen Bibliotheken und Module importieren: importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 Definition und Strukturanalyse eines Fuzzy-Neuronalen Netzwerks
Jan 22, 2024 pm 09:09 PM
Definition und Strukturanalyse eines Fuzzy-Neuronalen Netzwerks
Jan 22, 2024 pm 09:09 PM
Das Fuzzy-Neuronale Netzwerk ist ein Hybridmodell, das Fuzzy-Logik und neuronale Netzwerke kombiniert, um unscharfe oder unsichere Probleme zu lösen, die mit herkömmlichen neuronalen Netzwerken nur schwer zu bewältigen sind. Sein Design ist von der Unschärfe und Unsicherheit der menschlichen Wahrnehmung inspiriert und wird daher häufig in Steuerungssystemen, Mustererkennung, Data Mining und anderen Bereichen eingesetzt. Die Grundarchitektur eines Fuzzy-Neuronalen Netzwerks besteht aus einem Fuzzy-Subsystem und einem Neuronalen Subsystem. Das Fuzzy-Subsystem verwendet Fuzzy-Logik, um Eingabedaten zu verarbeiten und in Fuzzy-Sätze umzuwandeln, um die Unschärfe und Unsicherheit der Eingabedaten auszudrücken. Das neuronale Subsystem nutzt neuronale Netze zur Verarbeitung von Fuzzy-Sets für Aufgaben wie Klassifizierung, Regression oder Clustering. Durch die Interaktion zwischen dem Fuzzy-Subsystem und dem neuronalen Subsystem verfügt das Fuzzy-Neuronale Netzwerk über leistungsfähigere Verarbeitungsfähigkeiten und kann
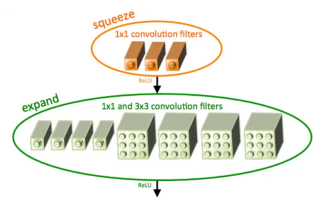 Einführung in SqueezeNet und seine Eigenschaften
Jan 22, 2024 pm 07:15 PM
Einführung in SqueezeNet und seine Eigenschaften
Jan 22, 2024 pm 07:15 PM
SqueezeNet ist ein kleiner und präziser Algorithmus, der eine gute Balance zwischen hoher Genauigkeit und geringer Komplexität schafft und sich daher ideal für mobile und eingebettete Systeme mit begrenzten Ressourcen eignet. Im Jahr 2016 schlugen Forscher von DeepScale, der University of California, Berkeley und der Stanford University SqueezeNet vor, ein kompaktes und effizientes Faltungs-Neuronales Netzwerk (CNN). In den letzten Jahren haben Forscher mehrere Verbesserungen an SqueezeNet vorgenommen, darunter SqueezeNetv1.1 und SqueezeNetv2.0. Verbesserungen in beiden Versionen erhöhen nicht nur die Genauigkeit, sondern senken auch die Rechenkosten. Genauigkeit von SqueezeNetv1.1 im ImageNet-Datensatz
 Bildrauschen mithilfe von Faltungs-Neuronalen Netzen
Jan 23, 2024 pm 11:48 PM
Bildrauschen mithilfe von Faltungs-Neuronalen Netzen
Jan 23, 2024 pm 11:48 PM
Faltungs-Neuronale Netze eignen sich gut für Aufgaben zur Bildrauschunterdrückung. Es nutzt die erlernten Filter, um das Rauschen zu filtern und so das Originalbild wiederherzustellen. In diesem Artikel wird die Methode zur Bildentrauschung basierend auf einem Faltungs-Neuronalen Netzwerk ausführlich vorgestellt. 1. Überblick über das Convolutional Neural Network Das Convolutional Neural Network ist ein Deep-Learning-Algorithmus, der eine Kombination aus mehreren Faltungsschichten, Pooling-Schichten und vollständig verbundenen Schichten verwendet, um Bildmerkmale zu lernen und zu klassifizieren. In der Faltungsschicht werden die lokalen Merkmale des Bildes durch Faltungsoperationen extrahiert und so die räumliche Korrelation im Bild erfasst. Die Pooling-Schicht reduziert den Rechenaufwand durch Reduzierung der Feature-Dimension und behält die Hauptfeatures bei. Die vollständig verbundene Schicht ist für die Zuordnung erlernter Merkmale und Beschriftungen zur Implementierung der Bildklassifizierung oder anderer Aufgaben verantwortlich. Das Design dieser Netzwerkstruktur macht das Faltungs-Neuronale Netzwerk für die Bildverarbeitung und -erkennung nützlich.
 Schritte zum Schreiben eines einfachen neuronalen Netzwerks mit Rust
Jan 23, 2024 am 10:45 AM
Schritte zum Schreiben eines einfachen neuronalen Netzwerks mit Rust
Jan 23, 2024 am 10:45 AM
Rust ist eine Programmiersprache auf Systemebene, die sich auf Sicherheit, Leistung und Parallelität konzentriert. Ziel ist es, eine sichere und zuverlässige Programmiersprache bereitzustellen, die für Szenarien wie Betriebssysteme, Netzwerkanwendungen und eingebettete Systeme geeignet ist. Die Sicherheit von Rust beruht hauptsächlich auf zwei Aspekten: dem Eigentumssystem und dem Kreditprüfer. Das Besitzsystem ermöglicht es dem Compiler, den Code zur Kompilierungszeit auf Speicherfehler zu überprüfen und so häufige Speichersicherheitsprobleme zu vermeiden. Indem Rust die Überprüfung der Eigentumsübertragungen von Variablen zur Kompilierungszeit erzwingt, stellt Rust sicher, dass Speicherressourcen ordnungsgemäß verwaltet und freigegeben werden. Der Borrow-Checker analysiert den Lebenszyklus der Variablen, um sicherzustellen, dass nicht mehrere Threads gleichzeitig auf dieselbe Variable zugreifen, wodurch häufige Sicherheitsprobleme bei der Parallelität vermieden werden. Durch die Kombination dieser beiden Mechanismen ist Rust in der Lage, Folgendes bereitzustellen
 Twin Neural Network: Prinzip- und Anwendungsanalyse
Jan 24, 2024 pm 04:18 PM
Twin Neural Network: Prinzip- und Anwendungsanalyse
Jan 24, 2024 pm 04:18 PM
Das Siamese Neural Network ist eine einzigartige künstliche neuronale Netzwerkstruktur. Es besteht aus zwei identischen neuronalen Netzen mit denselben Parametern und Gewichten. Gleichzeitig teilen die beiden Netzwerke auch die gleichen Eingabedaten. Dieses Design wurde von Zwillingen inspiriert, da die beiden neuronalen Netze strukturell identisch sind. Das Prinzip des siamesischen neuronalen Netzwerks besteht darin, bestimmte Aufgaben wie Bildabgleich, Textabgleich und Gesichtserkennung durch den Vergleich der Ähnlichkeit oder des Abstands zwischen zwei Eingabedaten auszuführen. Während des Trainings versucht das Netzwerk, ähnliche Daten benachbarten Regionen und unterschiedliche Daten entfernten Regionen zuzuordnen. Auf diese Weise kann das Netzwerk lernen, verschiedene Daten zu klassifizieren oder abzugleichen, um entsprechende Ergebnisse zu erzielen



