 Backend-Entwicklung
Backend-Entwicklung
 Python-Tutorial
Python-Tutorial
 Detaillierte Schritte zum Implementieren der Stapeldurchquerung eines Binärbaums in der richtigen Reihenfolge mit Python
Detaillierte Schritte zum Implementieren der Stapeldurchquerung eines Binärbaums in der richtigen Reihenfolge mit Python
Detaillierte Schritte zum Implementieren der Stapeldurchquerung eines Binärbaums in der richtigen Reihenfolge mit Python

使用堆栈无需递归就能遍历二叉树,下面是一个使用堆栈中序遍历二叉树的算法。
算法思路
1)创建一个空栈S。
2)将当前节点初始化为root
3)将当前节点推入S并设置current=current->left直到current为NULL
4)如果current为NULL且堆栈不为空,则
a)从堆栈中弹出顶部项目。
b)输出弹出的项目,设置current=popped_item->right
c)转到步骤3)。
5)如果current为NULL并且stack为空,那么算法结束。
算法实现步骤
1
/\
2 3
/\
4 5
步骤1创建一个空堆栈:S=NULL
步骤2将current设置为root的地址:current->1
步骤3推送当前节点并设置current=current->left
直到当前为NULL
当前->1
推1:堆栈S->1
当前->2
推2:堆栈>2,1
当前->4
推4:堆栈S>4、2、1
当前=NULL
步骤4从S弹出
a)弹出4:堆栈S->2,1
b)打印“4”
c)current=NULL/*right of 4*/并转到步骤3
由于current is NULL step 3没有做任何事情。
步骤4再次弹出。
a)弹出2:堆栈S->1
b)打印“2”
c)current->;5/*right of 2*/并转到步骤3
第3步将5推入堆栈并使当前为NULL
堆栈S->5,1
当前=NULL
步骤4从S弹出
a)弹出5:堆栈S->1
b)打印“5”
c)current=NULL/*right of 5*/并转到步骤3
由于current is NULL step 3没有做任何事情
步骤4再次弹出。
a)弹出1:堆栈S->NULL
b)打印“1”
c)当前->3/*1的右边*/
第3步将3推入堆栈并使当前为NULL
堆栈S->3
当前=NULL
步骤4从S弹出
a)弹出3:堆栈S->NULL
b)打印“3”
c)current=NULL/*3的右边*/
由于堆栈S为空且当前为NULL,因此遍历已完成。
Python实现堆栈中序遍历二叉树
class Node: def __init__(self,data): self.data=data self.left=None self.right=None def inOrder(root): current=root stack=[] while True: if current is not None: stack.append(current) current=current.left elif(stack): current=stack.pop() print(current.data,end="") current=current.right else: break print() root=Node(1) root.left=Node(2) root.right=Node(3) root.left.left=Node(4) root.left.right=Node(5) inOrder(root)
Das obige ist der detaillierte Inhalt vonDetaillierte Schritte zum Implementieren der Stapeldurchquerung eines Binärbaums in der richtigen Reihenfolge mit Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1383
1383
 52
52
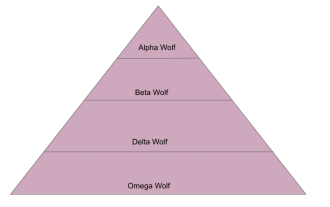 Eine eingehende Analyse des Grey Wolf Optimization Algorithm (GWO) und seiner Stärken und Schwächen
Jan 19, 2024 pm 07:48 PM
Eine eingehende Analyse des Grey Wolf Optimization Algorithm (GWO) und seiner Stärken und Schwächen
Jan 19, 2024 pm 07:48 PM
Der Grey Wolf Optimization Algorithm (GWO) ist ein bevölkerungsbasierter metaheuristischer Algorithmus, der die Führungshierarchie und den Jagdmechanismus grauer Wölfe in der Natur simuliert. Inspiration zum Grauwolf-Algorithmus 1. Graue Wölfe gelten als Spitzenprädatoren und stehen an der Spitze der Nahrungskette. 2. Graue Wölfe leben gerne in Gruppen (Gruppenleben), mit durchschnittlich 5-12 Wölfen in jedem Rudel. 3. Graue Wölfe haben eine sehr strenge soziale Dominanzhierarchie, wie unten gezeigt: Alpha-Wolf: Alpha-Wolf nimmt eine dominante Position in der gesamten Gruppe grauer Wölfe ein und hat das Recht, die gesamte Gruppe grauer Wölfe zu befehligen. Bei der Anwendung von Algorithmen ist Alpha Wolf eine der besten Lösungen, die vom Optimierungsalgorithmus erzeugte optimale Lösung. Beta-Wolf: Beta-Wolf berichtet regelmäßig an Alpha-Wolf und hilft Alpha-Wolf, die besten Entscheidungen zu treffen. In Algorithmusanwendungen kann Beta Wolf
 Erkunden Sie die Grundprinzipien und den Implementierungsprozess verschachtelter Sampling-Algorithmen
Jan 22, 2024 pm 09:51 PM
Erkunden Sie die Grundprinzipien und den Implementierungsprozess verschachtelter Sampling-Algorithmen
Jan 22, 2024 pm 09:51 PM
Der verschachtelte Stichprobenalgorithmus ist ein effizienter Bayes'scher statistischer Inferenzalgorithmus, der zur Berechnung des Integrals oder der Summation unter komplexen Wahrscheinlichkeitsverteilungen verwendet wird. Dabei wird der Parameterraum in mehrere Hyperwürfel mit gleichem Volumen zerlegt und schrittweise und iterativ einer der Hyperwürfel mit dem kleinsten Volumen „herausgeschoben“ und dann der Hyperwürfel mit Zufallsstichproben gefüllt, um den Integralwert der Wahrscheinlichkeitsverteilung besser abzuschätzen. Durch kontinuierliche Iteration kann der verschachtelte Stichprobenalgorithmus hochpräzise Integralwerte und Grenzen des Parameterraums erhalten, die auf statistische Probleme wie Modellvergleich, Parameterschätzung und Modellauswahl angewendet werden können. Die Kernidee dieses Algorithmus besteht darin, komplexe Integrationsprobleme in eine Reihe einfacher Integrationsprobleme umzuwandeln und sich dem wahren Integralwert zu nähern, indem das Volumen des Parameterraums schrittweise verringert wird. Bei jedem Iterationsschritt werden zufällig Stichproben aus dem Parameterraum entnommen
 Analysieren Sie die Prinzipien, Modelle und Zusammensetzung des Sparrow Search Algorithm (SSA)
Jan 19, 2024 pm 10:27 PM
Analysieren Sie die Prinzipien, Modelle und Zusammensetzung des Sparrow Search Algorithm (SSA)
Jan 19, 2024 pm 10:27 PM
Der Sparrow Search Algorithm (SSA) ist ein metaheuristischer Optimierungsalgorithmus, der auf dem Anti-Raub- und Futtersuchverhalten von Spatzen basiert. Das Futtersuchverhalten von Spatzen kann in zwei Haupttypen unterteilt werden: Produzenten und Aasfresser. Produzenten suchen aktiv nach Nahrungsmitteln, während Aasfresser um Nahrungsmittel von Produzenten konkurrieren. Prinzip des Sparrow-Suchalgorithmus (SSA) Beim Sparrow-Suchalgorithmus (SSA) achtet jeder Spatz genau auf das Verhalten seiner Nachbarn. Durch den Einsatz verschiedener Futtersuchstrategien sind Einzelpersonen in der Lage, die gespeicherte Energie effizient zu nutzen, um mehr Nahrung zu suchen. Darüber hinaus sind Vögel in ihrem Suchraum anfälliger für Raubtiere und müssen daher sicherere Orte finden. Vögel in der Mitte einer Kolonie können ihren eigenen Gefahrenbereich minimieren, indem sie in der Nähe ihrer Nachbarn bleiben. Wenn ein Vogel ein Raubtier entdeckt, alarmiert er es
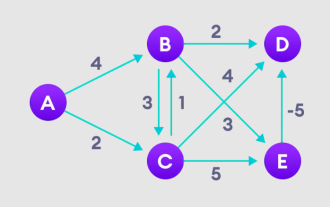 Detaillierte Erläuterung des Bellman-Ford-Algorithmus und der Implementierung in Python
Jan 22, 2024 pm 07:39 PM
Detaillierte Erläuterung des Bellman-Ford-Algorithmus und der Implementierung in Python
Jan 22, 2024 pm 07:39 PM
Der Bellman-Ford-Algorithmus kann den kürzesten Weg vom Zielknoten zu anderen Knoten im gewichteten Diagramm finden. Dies ist dem Dijkstra-Algorithmus sehr ähnlich. Der Bellman-Ford-Algorithmus kann Diagramme mit negativen Gewichten verarbeiten und ist hinsichtlich der Implementierung relativ einfach. Ausführliche Erläuterung des Prinzips des Bellman-Ford-Algorithmus: Der Bellman-Ford-Algorithmus findet iterativ neue Pfade, die kürzer als die überschätzten Pfade sind, indem er die Pfadlängen vom Startscheitelpunkt zu allen anderen Scheitelpunkten überschätzt. Da wir die Pfadentfernung jedes Knotens aufzeichnen möchten, können wir sie in einem Array der Größe n speichern, wobei n auch die Anzahl der Knoten darstellt. Beispiel Abbildung 1. Wählen Sie den Startknoten aus, weisen Sie ihn unbegrenzt allen anderen Scheitelpunkten zu und zeichnen Sie den Pfadwert auf. 2. Besuchen Sie jede Kante und führen Sie Entspannungsoperationen durch, um den kürzesten Pfad kontinuierlich zu aktualisieren. 3. Wir brauchen
 Einführung in den Wu-Manber-Algorithmus und Python-Implementierungsanweisungen
Jan 23, 2024 pm 07:03 PM
Einführung in den Wu-Manber-Algorithmus und Python-Implementierungsanweisungen
Jan 23, 2024 pm 07:03 PM
Der Wu-Manber-Algorithmus ist ein String-Matching-Algorithmus zur effizienten Suche nach Strings. Es handelt sich um einen Hybridalgorithmus, der die Vorteile der Boyer-Moore- und Knuth-Morris-Pratt-Algorithmen kombiniert, um einen schnellen und genauen Mustervergleich zu ermöglichen. Schritt 1 des Wu-Manber-Algorithmus: Erstellen Sie eine Hash-Tabelle, die jede mögliche Teilzeichenfolge des Musters der Musterposition zuordnet, an der diese Teilzeichenfolge auftritt. 2. Diese Hash-Tabelle wird verwendet, um mögliche Startpositionen von Mustern im Text schnell zu identifizieren. 3. Durchlaufen Sie den Text und vergleichen Sie jedes Zeichen mit dem entsprechenden Zeichen im Muster. 4. Wenn die Zeichen übereinstimmen, können Sie zum nächsten Zeichen wechseln und den Vergleich fortsetzen. 5. Wenn die Zeichen nicht übereinstimmen, können Sie mithilfe einer Hash-Tabelle das nächste mögliche Zeichen im Muster ermitteln.
 Numerische Optimierungsprinzipien und Analyse des Whale Optimization Algorithm (WOA)
Jan 19, 2024 pm 07:27 PM
Numerische Optimierungsprinzipien und Analyse des Whale Optimization Algorithm (WOA)
Jan 19, 2024 pm 07:27 PM
Der Whale Optimization Algorithm (WOA) ist ein von der Natur inspirierter metaheuristischer Optimierungsalgorithmus, der das Jagdverhalten von Buckelwalen simuliert und zur Optimierung numerischer Probleme eingesetzt wird. Der Whale Optimization Algorithm (WOA) beginnt mit einer Reihe zufälliger Lösungen und optimiert basierend auf einem zufällig ausgewählten Suchagenten oder der bisher besten Lösung durch Positionsaktualisierungen des Suchagenten in jeder Iteration. Inspiration für den Waloptimierungsalgorithmus Der Waloptimierungsalgorithmus ist vom Jagdverhalten von Buckelwalen inspiriert. Buckelwale bevorzugen oberflächennahe Nahrung wie Krill und Fischschwärme. Daher sammeln Buckelwale Nahrung und bilden ein Blasennetzwerk, indem sie bei der Jagd Blasen in einer Spirale von unten nach oben blasen. Bei einem „Aufwärtsspiral“-Manöver taucht der Buckelwal etwa 12 m tief, beginnt dann, eine spiralförmige Blase um seine Beute zu bilden und schwimmt nach oben
 Welche Rolle spielt der Informationsgewinn im ID3-Algorithmus?
Jan 23, 2024 pm 11:27 PM
Welche Rolle spielt der Informationsgewinn im ID3-Algorithmus?
Jan 23, 2024 pm 11:27 PM
Der ID3-Algorithmus ist einer der grundlegenden Algorithmen beim Lernen von Entscheidungsbäumen. Es wählt den besten Teilungspunkt aus, indem es den Informationsgewinn jedes Features berechnet, um einen Entscheidungsbaum zu erstellen. Der Informationsgewinn ist ein wichtiges Konzept im ID3-Algorithmus, der zur Messung des Beitrags von Merkmalen zur Klassifizierungsaufgabe verwendet wird. In diesem Artikel werden das Konzept, die Berechnungsmethode und die Anwendung des Informationsgewinns im ID3-Algorithmus ausführlich vorgestellt. 1. Das Konzept der Informationsentropie Informationsentropie ist ein Konzept der Informationstheorie, das die Unsicherheit von Zufallsvariablen misst. Für eine diskrete Zufallsvariablenzahl stellt p(x_i) die Wahrscheinlichkeit dar, dass die Zufallsvariable X den Wert x_i annimmt. Brief
 SIFT-Algorithmus (Scale Invariant Features).
Jan 22, 2024 pm 05:09 PM
SIFT-Algorithmus (Scale Invariant Features).
Jan 22, 2024 pm 05:09 PM
Der Scale Invariant Feature Transform (SIFT)-Algorithmus ist ein Merkmalsextraktionsalgorithmus, der in den Bereichen Bildverarbeitung und Computer Vision verwendet wird. Dieser Algorithmus wurde 1999 vorgeschlagen, um die Objekterkennung und die Matching-Leistung in Computer-Vision-Systemen zu verbessern. Der SIFT-Algorithmus ist robust und genau und wird häufig in der Bilderkennung, dreidimensionalen Rekonstruktion, Zielerkennung, Videoverfolgung und anderen Bereichen eingesetzt. Es erreicht Skaleninvarianz, indem es Schlüsselpunkte in mehreren Skalenräumen erkennt und lokale Merkmalsdeskriptoren um die Schlüsselpunkte herum extrahiert. Zu den Hauptschritten des SIFT-Algorithmus gehören die Skalenraumkonstruktion, die Erkennung von Schlüsselpunkten, die Positionierung von Schlüsselpunkten, die Richtungszuweisung und die Generierung von Merkmalsdeskriptoren. Durch diese Schritte kann der SIFT-Algorithmus robuste und einzigartige Merkmale extrahieren und so eine effiziente Bildverarbeitung erreichen.



