Gleichverteilung versus naives Mischen?

PHP-Redakteur Xiaoxin wird den Zusammenhang zwischen „gleichmäßiger Verteilung und naivem Mischen“ aufdecken. In der Informatik ist das Mischen eine wichtige Operation, die häufig zum Randomisieren von Daten oder Sammlungen verwendet wird. Gleichverteilung bedeutet, dass die Zufallszahlenverteilung innerhalb eines bestimmten Bereichs durchschnittlich ist. Kann das Mischen also eine gleichmäßige Verteilung gewährleisten? Die Antwort ist nicht einfach, also lassen Sie uns diese Frage gemeinsam untersuchen.
Frageninhalt
Ich mische ein 3-Int-Array 6 Millionen Mal. Ich zeichne jede Permutation des Arrays in einer Karte auf. Unten ist der Code mit go.
package main
import (
"fmt"
"math/rand"
"time"
)
func randrange(min, max int) int {
return rand.intn(max-min+1) + min
}
func naiveshuffle(arr *[3]int) {
for i := 0; i < 3; i++ {
e := randrange(0, 2)
arr[e], arr[i] = arr[i], arr[e]
}
}
func main() {
rand.seed(time.now().unixnano())
m := make(map[[3]int]int, 6)
arr := [3]int{-6,10,184}
for i := 1; i <= 6000000; i++ {
a := arr
naiveshuffle(&arr)
m[a]++
}
for k, v := range m {
fmt.println(k, ":", v)
}
}Da ich ein einfaches Mischen durchführe, verstehe ich, dass es nicht nicht zu einer gleichmäßig verteilten Permutation kommen sollte. Aber das habe ich bekommen:
[184 -6 10] : 1000074 [184 10 -6] : 1000764 [-6 10 184] : 1000766 [10 184 -6] : 998090 [-6 184 10] : 1000479 [10 -6 184] : 999827
Dies zeigt, dass jede der 6 möglichen Permutationen ungefähr 1 Million Mal vorkommt. Warum sieht die Verteilung, die ich erhalte, einheitlich aus?
BEARBEITEN: Code so geändert, dass nur einmal gesät wird. Ich bekomme jetzt:
[-6 184 10] : 999507 [184 -6 10] : 1000401 [10 -6 184] : 1002163 [10 184 -6] : 999236 [-6 10 184] : 999016 [184 10 -6] : 999677
Edit 2: Dank Hobbs wurde mir klar, dass ich einen dummen Fehler gemacht hatte. Ich sollte mischen a,而不是 arr. Ich bekomme jetzt:
[10 -6 184] : 1111056 [-6 10 184] : 888442 [184 -6 10] : 888576 [10 184 -6] : 1109896 [-6 184 10] : 1113148 [184 10 -6] : 888882
Workaround
Sie haben arr mehr als 6 Millionen Mal gemischt, ohne es zwischen den Mischvorgängen in seinen ursprünglichen Zustand zurückzusetzen – mit anderen Worten, Ihre 6 Millionen Versuche waren nicht unabhängig. Die . Obwohl die Permutationen jedes Mischvorgangs ungleichmäßig verteilt sind, führt das 6-Millionen-fache Stapeln dieser Permutationen übereinander zu einer Verteilung, die nahezu gleichmäßig ist.
Das obige ist der detaillierte Inhalt vonGleichverteilung versus naives Mischen?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 So überprüfen Sie den Datenverkehr auf einem Apple-Mobiltelefon
May 09, 2024 pm 06:00 PM
So überprüfen Sie den Datenverkehr auf einem Apple-Mobiltelefon
May 09, 2024 pm 06:00 PM
So überprüfen Sie die Datennutzung auf einem Apple-Mobiltelefon 1. Die spezifischen Schritte zum Überprüfen der Datennutzung auf einem Apple-Mobiltelefon sind wie folgt: Öffnen Sie die Einstellungen des Telefons. Klicken Sie auf die Schaltfläche Mobilfunk. Scrollen Sie auf der Mobilfunknetzseite nach unten, um die spezifische Datennutzung jeder Anwendung anzuzeigen. Klicken Sie auf „Übernehmen“, um auch zulässige Netzwerke festzulegen. 2. Schalten Sie das Telefon ein, suchen Sie die Einstellungsoption auf dem Telefondesktop und klicken Sie zum Aufrufen. Suchen Sie in der Einstellungsoberfläche in der Taskleiste unten nach „Mobilfunknetz“ und klicken Sie zum Aufrufen. Suchen Sie in der Mobilfunknetzschnittstelle auf der Seite die Option „Nutzung“ und klicken Sie zur Eingabe. 3. Eine andere Möglichkeit besteht darin, den Datenverkehr selbst über das Mobiltelefon zu überprüfen. Das Mobiltelefon kann jedoch nur die Gesamtnutzung sehen und den verbleibenden Datenverkehr nicht anzeigen: Schalten Sie das iPhone ein, suchen Sie die Option „Einstellungen“ und öffnen Sie sie. Wählen Sie „Biene“
 So deaktivieren Sie das Snapshot-Layout in Windows 11_ Tipps, wie Sie das Snapshot-Layout in Win11 nicht verwenden
May 08, 2024 pm 06:46 PM
So deaktivieren Sie das Snapshot-Layout in Windows 11_ Tipps, wie Sie das Snapshot-Layout in Win11 nicht verwenden
May 08, 2024 pm 06:46 PM
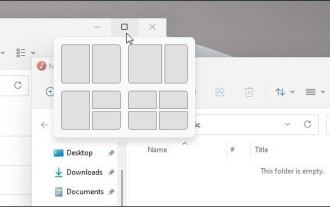
Das Win11-System hat das neue [Snapshot-Layout] angekündigt, das Benutzern über die Schaltfläche [Maximieren] verschiedene Fensterlayoutoptionen bietet, sodass Benutzer aus mehreren Layoutvorlagen auswählen können, um zwei, drei oder vier geöffnete Anwendungen auf dem Bildschirm anzuzeigen. Dies ist eine Verbesserung gegenüber dem Ziehen mehrerer Fenster an die Seiten des Bildschirms und dem anschließenden manuellen Anpassen aller Fenster. [SnapGroups] speichert die Sammlung der vom Benutzer verwendeten Apps und deren Layout, sodass der Benutzer problemlos zu dieser Einstellung zurückkehren kann, wenn er anhalten und etwas anderes tun muss. Wenn jemand einen Monitor verwendet, den der Benutzer beim erneuten Andocken ausstecken muss, wird auch das zuvor verwendete Snapshot-Layout wiederhergestellt. Um das Snapshot-Layout zu verwenden, können wir zum Starten die Tastenkombination Windows-Taste+Z verwenden
 So zeigen Sie Reiseaufzeichnungen auf Amap an
May 05, 2024 pm 05:21 PM
So zeigen Sie Reiseaufzeichnungen auf Amap an
May 05, 2024 pm 05:21 PM
Schritte zum Anzeigen von Reisedatensätzen auf Amap: 1. Melden Sie sich bei Amap an. 2. Geben Sie „Meine“ → „Meine Reise“ ein. 4. Klicken Sie, um Details anzuzeigen. .
 So sortieren Sie die Listenseite alphabetisch in vscode. So sortieren Sie die Listenseite alphabetisch in vscode
May 09, 2024 am 09:40 AM
So sortieren Sie die Listenseite alphabetisch in vscode. So sortieren Sie die Listenseite alphabetisch in vscode
May 09, 2024 am 09:40 AM
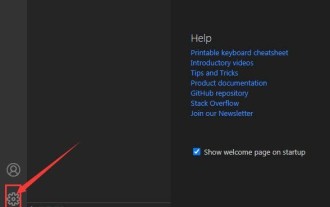
1. Klicken Sie nach dem Öffnen der vscode-Benutzeroberfläche zunächst auf die Symbolschaltfläche „Einstellungen“ in der unteren linken Ecke der Seite. 2. Klicken Sie dann in der Dropdown-Seitenspalte auf die Option „Einstellungen“. 3. Suchen Sie dann im Sprungfenster nach der Option „Explorer“. 4. Klicken Sie abschließend auf der rechten Seite der Seite auf die Option „OpenEditorsnaming“, wählen Sie die alphabetische Schaltfläche auf der Dropdown-Seite aus und speichern Sie die Einstellungen, um die alphabetische Sortierung abzuschließen
 Der Vorgang zum Erstellen eines flaschenartigen Textlayouteffekts mit KI
May 06, 2024 pm 02:28 PM
Der Vorgang zum Erstellen eines flaschenartigen Textlayouteffekts mit KI
May 06, 2024 pm 02:28 PM
1. Öffnen Sie das Materialbild einer Flasche in AI und geben Sie nebenbei den Textinhalt ein, der erstellt werden soll. 2. Löschen Sie die Füllfarbe der Flasche und streichen Sie nur darüber, um einen hohlen, geschlossenen Pfad zu bilden. 3. Passen Sie Schriftgröße, Schriftart und Zeilenabstand des Textes an und ordnen Sie die Flaschenebenen nach oben an. 4. Wählen Sie gleichzeitig den Text und die Flasche aus, klicken Sie auf „Objekt-Umschlagverzerrung“ – „Mit Objekt der obersten Ebene erstellen“ und Sie erhalten eine flaschenförmige Textgruppe. 5. Doppelklicken Sie auf den Text, um in den Isolationsmodus zu wechseln. Sie können den Textinhalt ändern und die Farbe ändern. Nach der Änderung wird die Flaschenform beim Verlassen des Isolationsmodus nicht beeinträchtigt. Der Endeffekt ist wie folgt:
 So legen Sie den Klingelton in AI fest – die spezifische Methode zum Festlegen des Klingeltons in AI
May 06, 2024 pm 05:58 PM
So legen Sie den Klingelton in AI fest – die spezifische Methode zum Festlegen des Klingeltons in AI
May 06, 2024 pm 05:58 PM
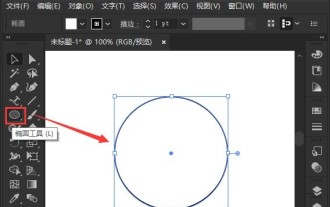
1. Klicken Sie nach dem Öffnen der Benutzeroberfläche zunächst auf das Ellipsen-Werkzeug, um einen perfekten Kreis zu zeichnen. 2. Klicken Sie links auf die Schaltfläche „Pfadtext“ und geben Sie Text entlang des kreisförmigen Rahmens ein. 3. Wählen Sie den Buchstaben aus und öffnen Sie das Zeichen Bedienfeld und stellen Sie die Schriftgröße auf 20,7 pt4 ein. Wählen Sie den Kreis aus, klicken Sie im Effektmenü auf 3D-Optionen und wählen Sie die Schaltfläche „Rotation“ aus. 5. Stellen Sie in den geöffneten 3D-Rotationsoptionseinstellungen die Positionsoption auf „Benutzerdefinierter Rotationseffekt“ ein und ändern Sie die Parameter und klicken Sie zum Speichern auf OK. 6. Schließlich ist es ein Ring. Fügen Sie dem Text einfach einen roten Fülleffekt hinzu
 So verwenden Sie Matplotlib zum Generieren von Diagrammen in Python
May 05, 2024 pm 07:54 PM
So verwenden Sie Matplotlib zum Generieren von Diagrammen in Python
May 05, 2024 pm 07:54 PM
Um Matplotlib zum Generieren von Diagrammen in Python zu verwenden, gehen Sie folgendermaßen vor: Installieren Sie die Matplotlib-Bibliothek. Importieren Sie Matplotlib und verwenden Sie die Funktion plt.plot(), um den Plot zu generieren. Passen Sie Diagramme an, legen Sie Titel, Beschriftungen, Raster, Farben und Markierungen fest. Verwenden Sie die Funktion plt.savefig(), um das Diagramm in einer Datei zu speichern.
 Kann ich beim Zusammenbau eines Computers eine drahtlose Netzwerkkarte anschließen?
May 08, 2024 am 09:13 AM
Kann ich beim Zusammenbau eines Computers eine drahtlose Netzwerkkarte anschließen?
May 08, 2024 am 09:13 AM
Kann ich beim Zusammenbau eines Computers eine drahtlose Netzwerkkarte anschließen? Zunächst einmal sollte die drahtlose Netzwerkkarte, von der Sie hier sprechen, eine drahtlose 2G/3G/4G-Netzwerkkarte sein, also eine drahtlose Netzwerkkarte, oder? Meine Antwort ist ja. Sie benötigen jedoch auch einen AP, der drahtlose USB-Netzwerkkarten unterstützt, z. B.: (nur für Jiuli-Verwendung, kein empfohlenes Produkt) Kann ich eine drahtlose Netzwerkkarte verwenden, um auf das Internet zuzugreifen, indem ich einen Desktop-Computer zusammenbaue? Netzwerkkarten sind für moderne Computer unerlässlich. Ohne eine Netzwerkkarte können Sie nicht auf das Internet zugreifen, unabhängig davon, ob es sich um eine integrierte Netzwerkkarte, eine unabhängige Netzwerkkarte oder eine drahtlose Netzwerkkarte handelt. Beim Zusammenbau eines Computers wird in der Regel keine separate Netzwerkkarte eingebaut, da die aktuellen Mainboards über integrierte Netzwerkkarten verfügen und somit keine Notwendigkeit besteht, eine weitere zu kaufen. Allerdings können die jetzt zusammengebauten Computer keinen drahtlosen Internetzugang wie Laptops nutzen, da diese vorhanden sind Ist keine WLAN-Netzwerkkarte installiert, können Sie dies nach Ihren eigenen Bedürfnissen tun






