Bei diesem Artikel handelt es sich um eine Studie zur Verbesserung der Skalierbarkeit der Optimierung nullter Ordnung. Der Code ist Open Source und das Papier wurde von ICLR 2024 angenommen.
Heute möchte ich einen Artikel mit dem Titel „DeepZero: Scaling up Zeroth-Order Optimization for Deep Model Training“ vorstellen, der in Zusammenarbeit mit der Michigan State University und dem Lawrence Livermore National Laboratory erstellt wurde. Dieses Papier wurde kürzlich von der ICLR 2024-Konferenz angenommen und das Forschungsteam hat den Code als Open Source bereitgestellt. Das Hauptziel dieses Artikels besteht darin, Optimierungstechniken nullter Ordnung im Deep-Learning-Modelltraining zu erweitern. Die Optimierung nullter Ordnung ist eine Optimierungsmethode, die nicht auf Gradienteninformationen basiert und hochdimensionale Parameterräume und komplexe Modellstrukturen besser verarbeiten kann. Bestehende Optimierungsmethoden nullter Ordnung stehen jedoch beim Umgang mit Deep-Learning-Modellen vor Skalierungs- und Effizienzproblemen. Um diese Herausforderungen anzugehen, schlug das Forschungsteam das DeepZero-Framework vor. Dieses Framework kann das Training umfangreicher Deep-Learning-Modelle effizient bewältigen, indem es neue Stichprobenstrategien und adaptive Anpassungsmechanismen einführt. DeepZero nutzt die Optimierung nullter Ordnung und kombiniert verteilte Rechen- und Parallelisierungstechnologie, um das Training zu beschleunigen ://www.optml-group.com/posts/deepzero_iclr24
1. Hintergrund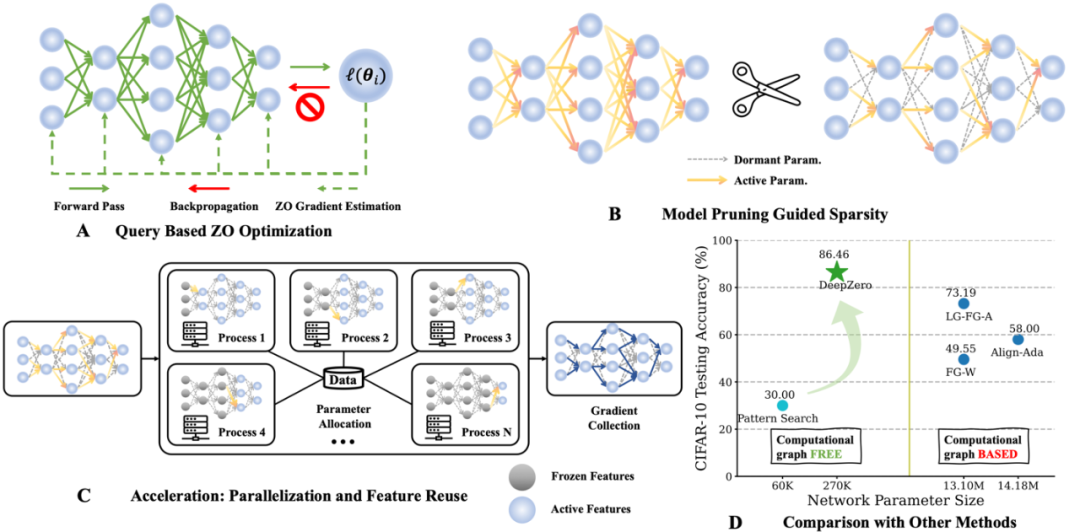
: Modelle des maschinellen Lernens können mit komplexen Simulatoren oder Experimenten gekoppelt sein. Interaktionen, bei denen das zugrunde liegende System nicht differenzierbar ist.
Black-Box-Learning-Szenario: Wenn ein Deep-Learning-Modell (Deep Learning) in eine API eines Drittanbieters integriert wird, z. B. gegnerische Angriffe und Abwehrmaßnahmen gegen Black-Box-Deep-Learning-Modelle und Black-Box-Prompt-Learning von Sprachmodelldiensten.
: Der prinzipielle Backpropagation-Mechanismus zur Berechnung von Gradienten erster Ordnung wird möglicherweise nicht unterstützt, wenn Deep-Learning-Modelle auf Hardwaresystemen implementiert werden.
2. Gradientenschätzung nullter Ordnung: RGE oder CGE?
Der Optimierer nullter Ordnung interagiert mit der Zielfunktion nur, indem er Eingaben übermittelt und entsprechende Funktionswerte empfängt. Es gibt zwei Hauptmethoden zur Gradientenschätzung: Koordinatengradientenschätzung (CGE) und Zufallsgradientenschätzung (RGE), wie unten gezeigt:
die Optimierungsvariable darstellt (z. B. neuronale Schätzung des Gradienten erster Ordnung). der Modellparameter des Netzwerks).
In (RGE) stellteinen zufälligen Störungsvektor dar, der beispielsweise aus einer Standard-Gauß-Verteilung stammt; ist die Störungsgröße (auch als Glättungsparameter bekannt); q ist die Anzahl der Zufallsrichtungen, die zum Erhalten der Endlichkeit verwendet werden Unterschied.
In (CGE) stellt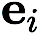 
die Standardbasisvektoren dar und 
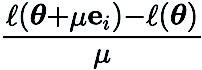liefert eine Finite-Differenzen-Schätzung der partiellen Ableitungen von 
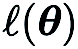an den entsprechenden Koordinaten.
Im Vergleich zu CGE bietet RGE die Flexibilität, die Anzahl der Funktionsauswertungen zu reduzieren. Trotz seiner hohen Abfrageeffizienz ist es immer noch ungewiss, ob RGE beim Training tiefer Modelle von Grund auf eine zufriedenstellende Genauigkeit bieten kann. Zu diesem Zweck haben wir eine Untersuchung durchgeführt, bei der wir kleine Faltungs-Neuronale Netze (CNN) unterschiedlicher Größe auf CIFAR-10 mithilfe von RGE und CGE trainiert haben. Wie in der folgenden Abbildung gezeigt, kann CGE eine Testgenauigkeit erreichen, die mit einem Optimierungstraining erster Ordnung vergleichbar ist, und ist deutlich besser als RGE. Außerdem ist es zeiteffizienter als RGE.
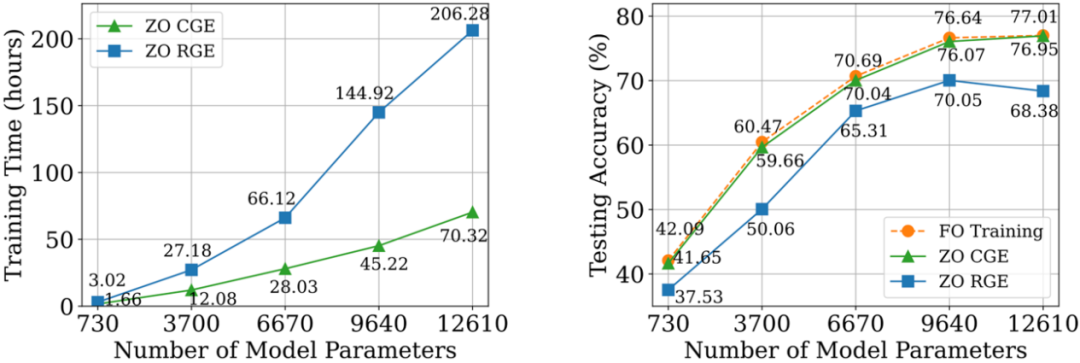
Basierend auf den Vorteilen von CGE gegenüber RGE in Bezug auf Genauigkeit und Recheneffizienz, Wir wählen CGE als bevorzugten Gradientenschätzer nullter Ordnung. Allerdings bleibt die Abfragekomplexität von CGE ein Engpass, da sie mit der Modellgröße skaliert.
3. Deep-Learning-Framework nullter Ordnung: DeepZero
Nach unserem besten Wissen hat keine frühere Arbeit die Wirksamkeit der ZO-Optimierung gezeigt, ohne die Leistung beim Training tiefer neuronaler Netze (DNN) erheblich zu verringern. Um dieses Hindernis zu überwinden, haben wir DeepZero entwickelt, ein prinzipielles Deep-Learning-Framework zur Optimierung nullter Ordnung, das die Optimierung nullter Ordnung von Grund auf auf das Training neuronaler Netzwerke erweitern kann.
a) Modellbereinigung nullter Ordnung (ZO-GraSP): Ein zufällig initialisiertes dichtes neuronales Netzwerk enthält oft ein hochwertiges, spärliches Subnetzwerk. Die effektivsten Beschneidungsmethoden beinhalten jedoch ein Modelltraining als Zwischenschritt. Daher eignen sie sich nicht für die Suche nach Sparsity durch Optimierung nullter Ordnung. Um die oben genannten Herausforderungen zu bewältigen, haben wir uns von einer schulungsfreien Beschneidungsmethode namens Initialisierungsbeschneiden inspirieren lassen. Unter diesen Methoden wird Gradient Signal Preserving (GraSP) ausgewählt, eine Methode zur Identifizierung der Sparsity-Priorität neuronaler Netze durch zufällige Initialisierung des Gradientenflusses des Netzes.
b) Sparse Gradient: Um die Genauigkeitsvorteile des Trainings dichter Modelle beizubehalten, integrieren wir in CGE Gradient Sparsity anstelle von Weight Sparsity. Dadurch wird sichergestellt, dass wir ein dichtes Modell im Gewichtsraum trainieren, anstatt ein spärliches Modell. Konkret verwenden wir ZO-GraSP, um schichtweise Pruning Ratios (LPRs) zu bestimmen, die die DNN-Kompressibilität erfassen können, und dann kann die Optimierung nullter Ordnung dichte Modelle trainieren, indem die Teilparametergewichte des Modells kontinuierlich iterativ aktualisiert werden, wobei das spärliche Gradientenverhältnis vorliegt durch LPRs bestimmt. c)
Feature-Wiederverwendung: Da CGE jeden Parameter elementweise stört, kann es die Features unmittelbar vor der Störungsschicht wiederverwenden und die verbleibende Vorwärtsausbreitungsoperation ausführen , anstatt von der Eingabeebene aus zu beginnen. Empirisch kann CGE mit Wiederverwendung von Funktionen eine Reduzierung der Trainingszeit um mehr als das Doppelte bewirken. d)
Front-Pass-Parallelisierung: CGE unterstützt die Parallelisierung des Modelltrainings. Diese Entkopplungseigenschaft ermöglicht eine Vorwärtsskalierung der Ausbreitung über verteilte Maschinen hinweg und erhöht so die Trainingsgeschwindigkeit nullter Ordnung erheblich.
4. Experimentelle Analysea) Bildklassifizierung
Auf dem CIFAR-10-Datensatz vergleichen wir ResNet-20, das von DeepZero trainiert wurde, mit zwei Varianten, die durch Optimierung erster Ordnung trainiert wurden:
(1) Dense ResNet -20
erhalten durch Optimierungstraining erster Ordnung (2) Sparse ResNet-20, erhalten durch FO-GraSP durch Optimierungstraining erster Ordnung, wie in der folgenden Abbildung dargestellt, allerdings bei 80 % bis 99 % spärlich Im Intervall im Vergleich zu (1) Das mit DeepZero trainierte Modell weist immer noch eine Genauigkeitslücke auf. Dies verdeutlicht die Herausforderungen der ZO-Optimierung für tiefes Modelltraining, bei dem Implementierungen mit hoher Sparsity erwünscht sind. Es ist erwähnenswert, dass DeepZero (2) im Sparsity-Intervall von 90 % bis 99 % übertrifft,
was die Überlegenheit von Gradient Sparsity gegenüber Weight Sparsity in DeepZero demonstriert.
b) Black-Box-Verteidigung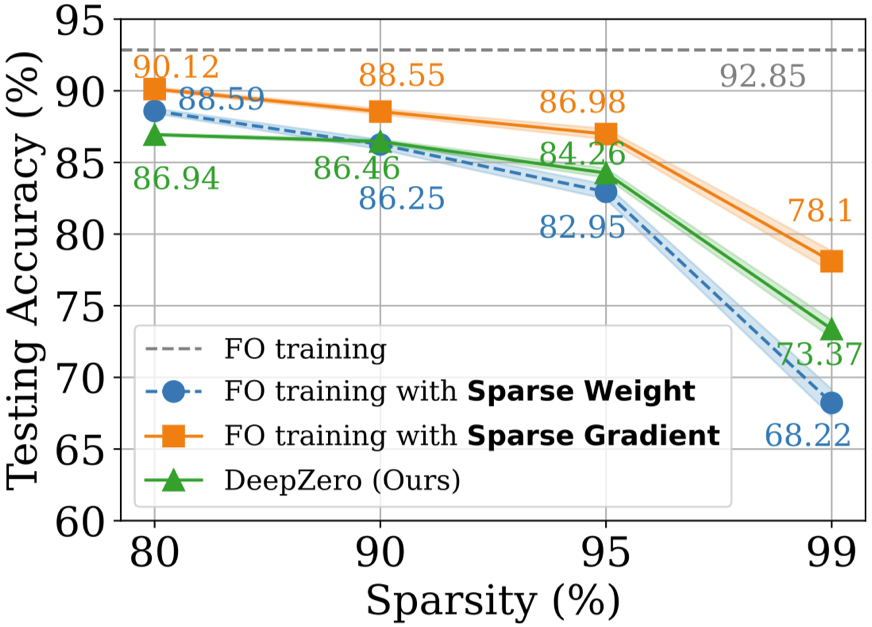
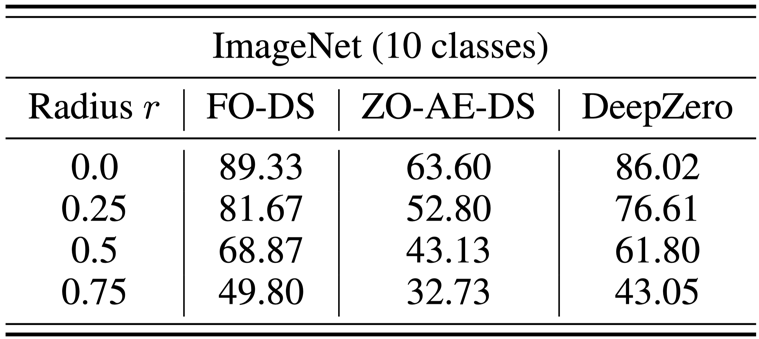
Das Black-Box-Verteidigungsproblem tritt auf, wenn der Besitzer eines Modells nicht bereit ist, Modelldetails mit dem Verteidiger zu teilen. Dies stellt eine Herausforderung für bestehende Algorithmen zur Robustheitsverbesserung dar, die White-Box-Modelle mithilfe von Optimierungstraining erster Ordnung direkt verbessern. Um diese Herausforderung zu bewältigen, wird ZO-AE-DS vorgeschlagen, das einen AutoEncoder (AE) zwischen der White-Box-Denoising-Smoothing-(DS)-Verteidigungsoperation und dem Black-Box-Bildklassifizierer einführt, um ZO-dimensionale Herausforderungen des Trainings zu lösen. ZO-AE-DS hat den Nachteil, dass es schwierig ist, auf hochauflösende Datensätze (z. B. ImageNet) zu skalieren, da die Verwendung von AE die Genauigkeit der in den Black-Box-Bildklassifikator eingegebenen Bilder beeinträchtigt und zu einer schlechten Verteidigungsleistung führt. Im Gegensatz dazu kann DeepZero Verteidigungsoperationen direkt erlernen integriert mit einem Black-Box-Klassifikator, ohne dass ein Autoencoder erforderlich ist. Wie in der Tabelle unten gezeigt, übertrifft DeepZero ZO-AE-DS bei allen Eingangsstörungsradien in Bezug auf die zertifizierte Genauigkeit (CA) durchweg.
c) Deep Learning gepaart mit Simulation
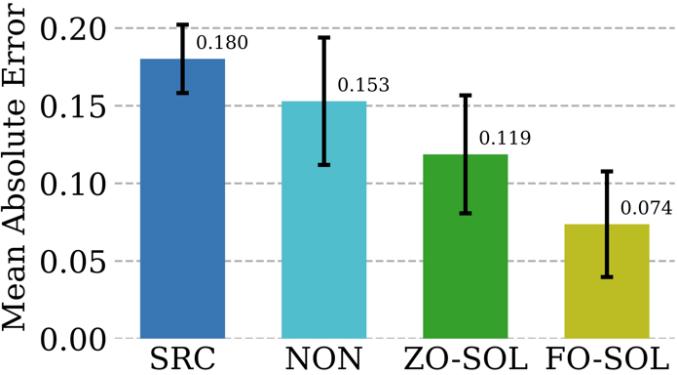
Numerische Methoden sind für die Bereitstellung physikalisch aussagekräftiger Simulationen unverzichtbar, haben aber ihre eigenen Herausforderungen: Diskretisierung erzeugt zwangsläufig numerische Fehler. Die Möglichkeit, neuronale Netze durch zyklisches interaktives Training mit einem iterativen Partial Differential Equation (PDE)-Löser zu korrigieren, wird als Solver-in-the-Loop (SOL) bezeichnet. Während sich bestehende Arbeiten auf die Verwendung oder Entwicklung differenzierbarer Simulatoren für das Modelltraining konzentrieren, Wir erweitern SOL durch die Nutzung von DeepZero, um die Verwendung mit nicht differenzierbaren oder Black-Box-Simulatoren zu ermöglichen. Die folgende Tabelle vergleicht die Testfehlerkorrekturleistung von ZO-SOL (implementiert von DeepZero) mit drei verschiedenen differenzierbaren Methoden:
(1) SRC (Low-Fidelity-Simulation ohne Fehlerkorrektur);
(2) NON (Nicht- interaktives Training, das außerhalb der Simulationsschleife unter Verwendung vorgenerierter Simulationsdaten mit niedriger und hoher Wiedergabetreue durchgeführt wird;
(3) FO-SOL (für SOL-Training erster Ordnung bei einem differenzierbaren Simulator).
Der Fehler für jede Testsimulation wird als mittlerer absoluter Fehler (MAE) der korrigierten Simulation im Vergleich zur High-Fidelity-Simulation berechnet. Die Ergebnisse zeigen, dass über DeepZero implementiertes ZO-SOL SRC und NON immer noch übertrifft und die Leistungslücke mit FO-SOL schließt, selbst wenn nur abfragebasierter Simulatorzugriff erfolgt. Die Leistung von ZO-SOL im Vergleich zu NON unterstreicht das Versprechen von ZO-SOL bei der Integration eines Black-Box-Simulators.
5. Zusammenfassung und Diskussion
In diesem Artikel wird ein optimiertes Deep-Learning-Framework nullter Ordnung (DeepZero) für Deep-Network-Training vorgestellt. Insbesondere integriert DeepZero die Koordinatengradientenschätzung, die durch Modellbereinigung nullter Ordnung verursachte Gradientensparsität, die Wiederverwendung von Merkmalen und die Frontpass-Parallelisierung in einen einheitlichen Trainingsprozess. Durch die Nutzung dieser Innovationen hat DeepZero Effizienz und Effektivität bei Aufgaben wie der Bildklassifizierung und einer Vielzahl praktischer Black-Box-Deep-Learning-Szenarien bewiesen. Darüber hinaus wird die Anwendbarkeit von DeepZero auf andere Bereiche untersucht, beispielsweise Anwendungen mit nicht differenzierbaren physikalischen Einheiten und Schulungen auf Geräten, auf denen Rechendiagramme und Backpropagation-Berechnungen nicht unterstützt werden.
Vorstellung des Autors
Zhang Yimeng, Doktorand in Informatik am OPTML-Labor der University of Michigan. Zu seinen Forschungsinteressen gehören generative KI, Multimodalität, Computer Vision, sichere KI und effiziente KI.
Das obige ist der detaillierte Inhalt vonICLR 2024 |. MSU und LLNL schlagen DeepZero vor, das erste optimierte Deep-Learning-Framework nullter Ordnung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
