
Im vorherigen Artikel haben wir hauptsächlich Techniken zur nichtlinearen Dimensionsreduktion zusammengefasst. In diesem Artikel werden wir gängige Techniken zur linearen Dimensionsreduktion zusammenfassen.
PCA ist eine weit verbreitete Technik zur Dimensionsreduktion, die hochdimensionale Datensätze in besser verwaltbare niedrigdimensionale Darstellungen umwandeln kann, während wichtige Merkmale der Daten erhalten bleiben. Durch die Identifizierung der Richtungen (Hauptkomponenten) mit der größten Varianz in den Daten kann PCA die Daten in diese Richtungen projizieren, um das Ziel der Dimensionsreduzierung zu erreichen.
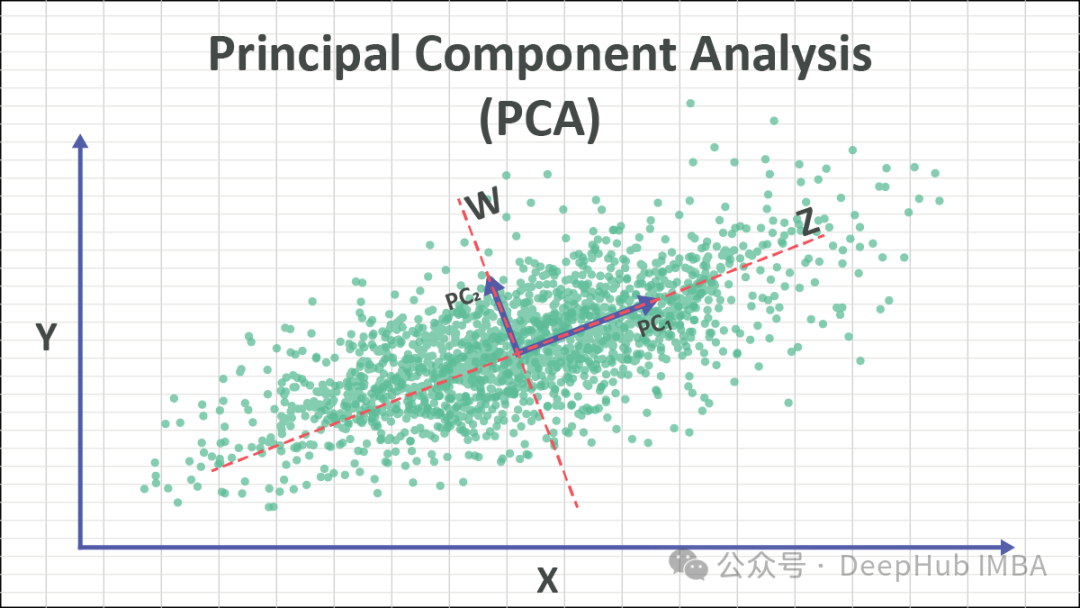
Die Kernidee von PCA besteht darin, die Originaldaten in ein neues Koordinatensystem umzuwandeln, um die Varianz der Daten zu maximieren. Diese neuen Achsen werden Hauptkomponenten genannt und sind lineare Kombinationen der ursprünglichen Merkmale. Durch die Beibehaltung der Hauptkomponente mit der größten Varianz bleiben im Wesentlichen die Schlüsselinformationen der Daten erhalten. Durch Verwerfen der Hauptkomponenten mit kleineren Varianzen kann der Zweck der Dimensionsreduktion erreicht werden.
PCA-Schritte sind wie folgt:
PCA kann für Aufgaben wie Datendimensionalitätsreduzierung, Merkmalsextraktion und Mustererkennung verwendet werden. Bei der Verwendung von PCA müssen Sie sicherstellen, dass die Daten die Grundannahme der linearen Trennbarkeit erfüllen, und die erforderliche Vorverarbeitung und das Verständnis der Daten durchführen, um genaue Dimensionsreduktionseffekte zu erzielen.
Faktoranalyse (FA) ist eine statistische Technik zur Identifizierung der zugrunde liegenden Struktur oder Faktoren unter den beobachteten Variablen. Sie zielt darauf ab, die latenten Faktoren aufzudecken, die für die gemeinsame Varianz zwischen den beobachteten Variablen verantwortlich sind. Letztendlich werden sie auf eine geringere Anzahl unabhängiger Variablen reduziert.
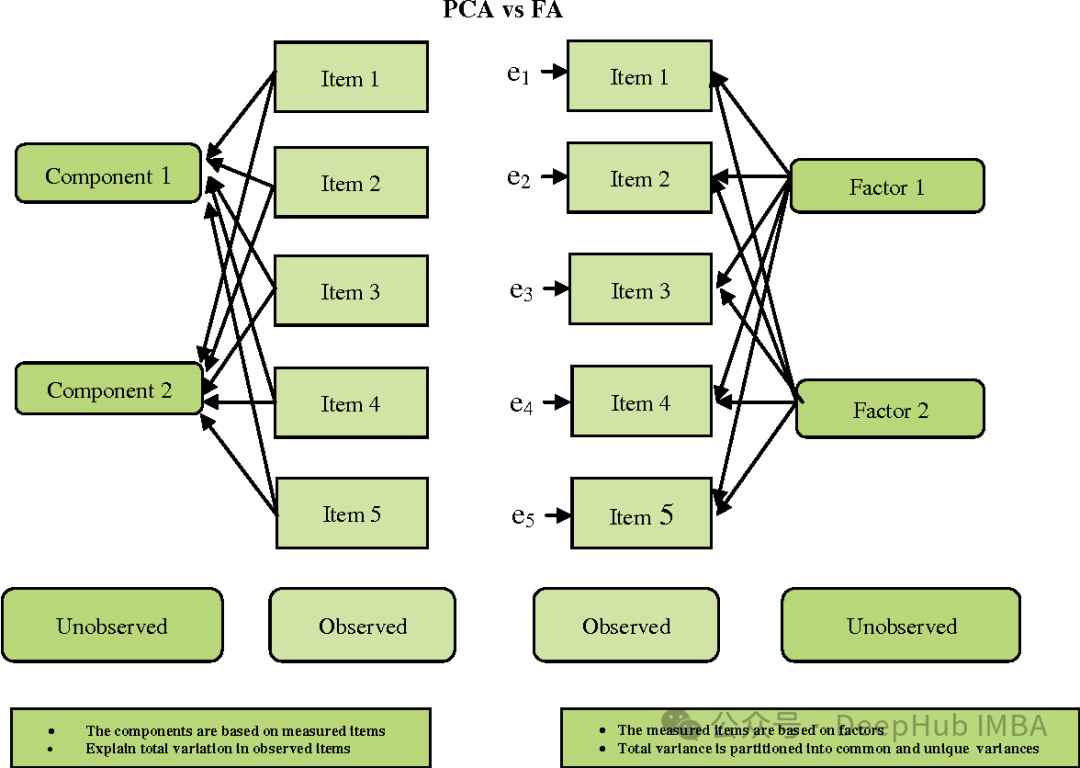
FA und PCA sind etwas ähnlich, es gibt jedoch einige wichtige Unterschiede:
Faktorenanalyse wird häufig in Bereichen wie Psychologie, Sozialwissenschaften und Marktforschung eingesetzt. Es hilft dabei, Datensätze zu vereinfachen, zugrunde liegende Strukturen zu entdecken und Messfehler zu reduzieren. Bei der Auswahl der Anzahl der Faktoren und der Rotationsmethode muss jedoch sorgfältig vorgegangen werden, um sicherzustellen, dass die Ergebnisse interpretierbar und gültig sind.
Die lineare Diskriminanzanalyse (LDA) ist eine überwachte Lerntechnologie zur Dimensionsreduktion und Merkmalsextraktion. Sie unterscheidet sich von der Hauptkomponentenanalyse (PCA), da sie nicht nur die Varianzstruktur der Daten berücksichtigt, sondern auch die Kategorieinformationen der Daten. LDA zielt darauf ab, eine Projektionsrichtung zu finden, die den Abstand zwischen verschiedenen Kategorien maximiert (Verbreitung zwischen den Klassen) und gleichzeitig den Abstand innerhalb derselben Kategorie minimiert (Verbreitung innerhalb der Klassen).
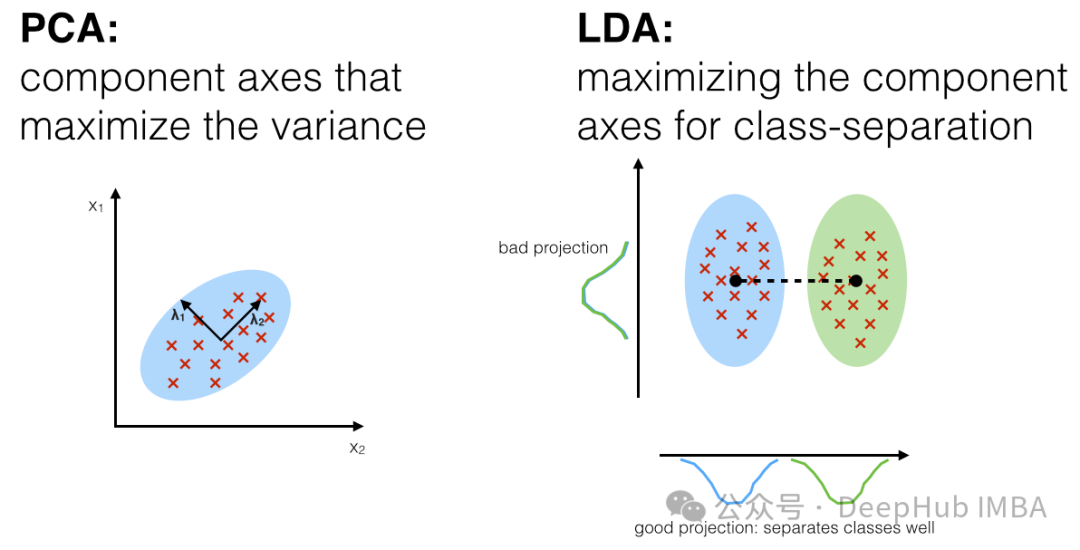
Die Hauptschritte von LDA sind wie folgt:
Der Vorteil von LDA besteht darin, dass es die Kategorieinformationen der Daten berücksichtigt, sodass die generierte Projektion die Unterschiede zwischen verschiedenen Kategorien besser unterscheiden kann. Es wird häufig in der Mustererkennung, Gesichtserkennung, Spracherkennung und anderen Bereichen eingesetzt. LDA kann beim Umgang mit mehreren Klassen und Klassenungleichgewichten auf einige Probleme stoßen und erfordert besondere Aufmerksamkeit.
Eigendekomposition (Eigenwertzerlegung) ist eine mathematische Technik zur Zerlegung quadratischer Matrizen. Es zerlegt eine quadratische Matrix in eine Menge von Eigenvektoren und das Produkt von Eigenwerten. Eigenvektoren stellen Richtungen dar, deren Richtung sich während der Transformation nicht ändert, während Eigenwerte die Skalierung entlang dieser Richtungen während der Transformation darstellen.
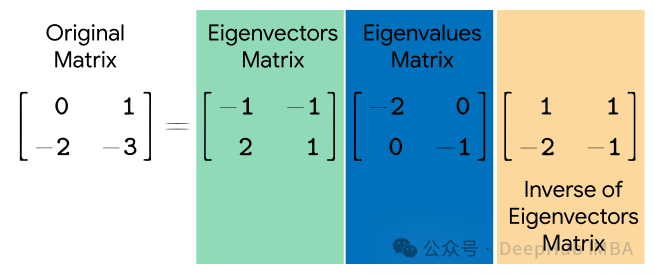
Gegeben eine quadratische Matrix AA, wird ihre Eigenwertzerlegung wie folgt ausgedrückt:

wobei Q eine Matrix ist, die aus Eigenvektoren von A besteht, Λ eine Diagonalmatrix ist und die Elemente auf ihrer Diagonale den Eigenwert darstellen von A.
Eigenwertzerlegung hat viele Anwendungen, einschließlich Hauptkomponentenanalyse (PCA), Eigengesichtserkennung, Spektralclusterung usw. Bei der PCA wird die Eigenwertzerlegung verwendet, um die Eigenvektoren der Kovarianzmatrix der Daten und damit die Hauptkomponenten der Daten zu ermitteln. Beim spektralen Clustering wird die Eigenwertzerlegung verwendet, um die Eigenvektoren der Ähnlichkeitskarte zu finden und so ein Clustering durchzuführen. Die Eigengesichtserkennung nutzt die Eigenwertzerlegung, um wichtige Merkmale in Gesichtsbildern zu identifizieren.
Obwohl die Eigenwertzerlegung in vielen Anwendungen sehr nützlich ist, können nicht alle quadratischen Matrizen eigenwertzerlegt werden. Beispielsweise können singuläre Matrizen oder nichtquadratische Matrizen nicht durch Eigenwerte zerlegt werden. Die Berechnung der Eigenwertzerlegung auf großen Matrizen kann sehr zeitaufwändig sein.
Singular Value Decomposition (SVD) ist eine wichtige Technik zur Matrixzerlegung. Es zerlegt eine Matrix in das Produkt von drei Matrizen, die die Transponierte einer orthogonalen Matrix, einer diagonalen Matrix und einer anderen orthogonalen Matrix sind.
Bei einer gegebenen m × n-Matrix AA wird ihre Singulärwertzerlegung wie folgt ausgedrückt:
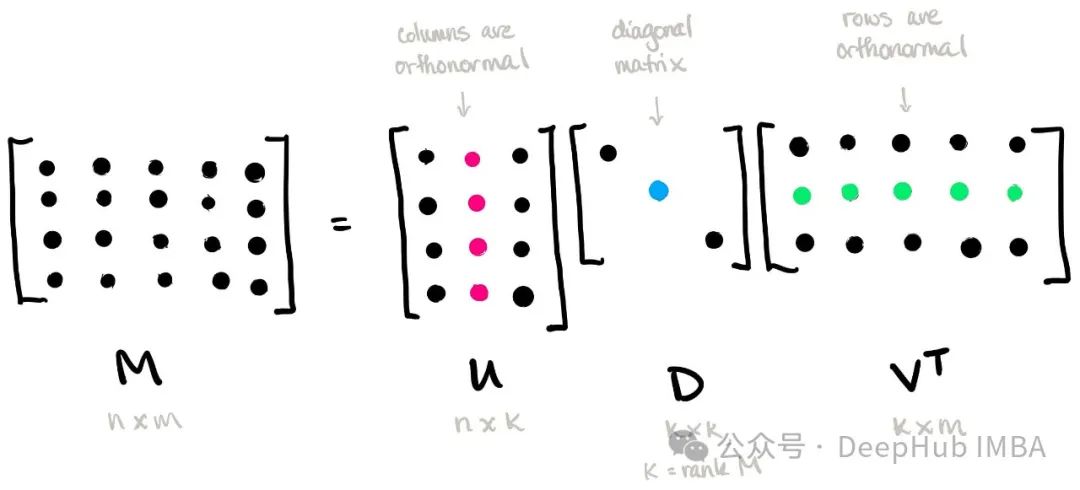
wobei U eine m × m-orthogonale Matrix ist, die als linke singuläre Vektormatrix bezeichnet wird; Σ eine m × n-Diagonalmatrix ist , und die Elemente auf seiner Diagonale werden Singulärwerte genannt; VT ist die Transponierte einer n × n-orthogonalen Matrix, die als rechte singuläre Vektormatrix bezeichnet wird.
Die Singularwertzerlegung hat ein breites Anwendungsspektrum, einschließlich Datenkomprimierung, Dimensionsreduktion, Matrix-Inverslösung, Empfehlungssystem usw. Bei der Dimensionsreduzierung werden nur Elemente mit größeren Singularwerten beibehalten, wodurch eine effektive Komprimierung und Darstellung der Daten erreicht werden kann. In Empfehlungssystemen kann die Beziehung zwischen Benutzern und Elementen durch Einzelwertzerlegung modelliert werden, um personalisierte Empfehlungen bereitzustellen.
Die Singulärwertzerlegung kann auch zur Lösung von Matrixinversen verwendet werden, insbesondere für singuläre Matrizen. Indem die Terme mit größeren Singulärwerten beibehalten werden, kann die inverse Matrix näherungsweise gelöst werden, wodurch das Problem der Invertierung der Singulärmatrix vermieden wird.
Truncated Singular Value Decomposition (TSVD) ist eine Variante der Singular Value Decomposition (SVD), die bei der Berechnung nur die wichtigsten Singularwertsummen entsprechender Singularvektoren behält und so Dimensionalität erreicht Reduzierung und Komprimierung von Daten.
Gegeben eine m × n-Matrix AA, wird ihre abgeschnittene Singulärwertzerlegung wie folgt ausgedrückt:

wobei Uk eine m × k-orthogonale Matrix ist, Σk eine k × k-Diagonalmatrix ist, VkT die Transponierte von a k × n ist Orthogonale Matrix, die der Beibehaltung der wichtigsten k Singulärwerte und entsprechenden Singulärvektoren entspricht.
Der Hauptvorteil von TSVD besteht darin, dass durch Beibehaltung der wichtigsten Einzelwerte und Einzelvektoren eine Dimensionsreduzierung und Komprimierung von Daten erreicht werden kann, wodurch die Speicher- und Rechenkosten gesenkt werden. Dies ist besonders bei der Arbeit mit großen Datensätzen nützlich, da der benötigte Speicherplatz und die Rechenzeit deutlich reduziert werden können.
TSVD hat Anwendungen in vielen Bereichen, einschließlich Bildverarbeitung, Signalverarbeitung, Empfehlungssystemen usw. In diesen Anwendungen kann TSVD verwendet werden, um die Dimensionalität von Daten zu reduzieren, Rauschen zu entfernen, Schlüsselmerkmale zu extrahieren usw.
Nicht-negative Matrixfaktorisierung (NMF) ist eine Technologie zur Datenzerlegung und Dimensionsreduktion. Ihr Merkmal ist, dass die durch Zerlegung erhaltenen Matrizen und Vektoren nicht negativ sind. Dies macht NMF in vielen Anwendungen nützlich, insbesondere in Bereichen wie Text Mining, Bildverarbeitung und Empfehlungssystemen.
Gegeben eine nicht negative Matrix VV, zerlegt NMF sie in die Produktform zweier nicht negativer Matrizen WW und HH:
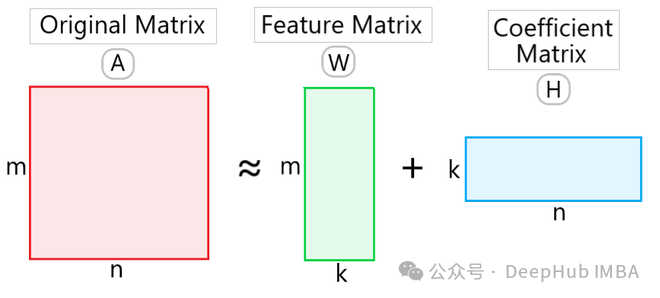
wobei W eine nicht negative Matrix von m × k ist, die als Basismatrix bezeichnet wird (Basismatrix) oder Merkmalsmatrix, H ist eine nicht negative k × n-Matrix, die als Koeffizientenmatrix bezeichnet wird. Dabei ist k die Dimension nach der Dimensionsreduktion.
Der Vorteil von NMF besteht darin, dass Zersetzungsergebnisse mit physikalischer Bedeutung erzielt werden können, da alle Elemente nicht negativ sind. Dies ermöglicht es NMF, latente Themen im Text Mining zu entdecken und Bildmerkmale in der Bildverarbeitung zu extrahieren. Darüber hinaus hat NMF auch die Funktion der Datendimensionalitätsreduzierung, wodurch die Dimensionalität und der Speicherplatz von Daten reduziert werden können.
NMF-Anwendungen umfassen Textthemenmodellierung, Bildsegmentierung und -komprimierung, Audiosignalverarbeitung, Empfehlungssysteme usw. In diesen Bereichen wird NMF häufig für Aufgaben wie Datenanalyse und Merkmalsextraktion sowie Informationsabruf und -klassifizierung eingesetzt.
Die Technologie zur linearen Dimensionsreduktion ist eine Art Technologie, mit der hochdimensionale Datensätze auf niedrigdimensionale Räume abgebildet werden. Die Kernidee besteht darin, die Hauptmerkmale des Datensatzes durch lineare Transformation beizubehalten. Diese linearen Dimensionsreduktionstechniken haben ihre einzigartigen Vorteile und Anwendbarkeit in verschiedenen Anwendungsszenarien, und die geeignete Methode kann basierend auf der Art der Daten und den Anforderungen der Aufgabe ausgewählt werden. PCA eignet sich beispielsweise für die unbeaufsichtigte Reduzierung der Datendimensionalität, während LDA für überwachte Lernaufgaben geeignet ist.
Basierend auf dem vorherigen Artikel haben wir 10 nichtlineare Dimensionsreduktionstechniken und 7 lineare Dimensionsreduktionstechniken vorgestellt Da der Algorithmus einfach, rechnerisch effizient und leicht zu verstehen und zu implementieren ist, kann er die nichtlineare Struktur in den Daten nicht erfassen, was zu Informationen führen kann ist verloren.
Nichtlineare Dimensionsreduktionstechnologie: Ordnet Daten durch nichtlineare Transformation einem niedrigdimensionalen Raum zu. Geeignet für Datensätze mit nichtlinearen Strukturen, z. B. auf einer Mannigfaltigkeit verteilte Datenpunkte, kann die Nichtlinearität in der Datenstruktur und den lokalen Beziehungen besser beibehalten werden Visualisierung; höhere Rechenkomplexität, die normalerweise mehr Rechenressourcen und Zeit erfordert.
Wenn die Daten linear trennbar sind oder die Rechenressourcen begrenzt sind, kann die Technologie zur linearen Dimensionsreduktion ausgewählt werden. Wenn die Daten komplexe nichtlineare Strukturen enthalten oder eine bessere Visualisierung erfordern, können Sie die Verwendung nichtlinearer Dimensionsreduktionstechnologie in Betracht ziehen. In der Praxis können Sie auch verschiedene Methoden ausprobieren und basierend auf dem tatsächlichen Effekt die am besten geeignete Technologie zur Dimensionsreduzierung auswählen.
Das obige ist der detaillierte Inhalt vonZusammenfassung von sieben häufig verwendeten Techniken zur linearen Dimensionsreduktion beim maschinellen Lernen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Welche Protokolle umfasst das SSL-Protokoll?
Welche Protokolle umfasst das SSL-Protokoll?
 Tutorial zur Cloud-Server-Nutzung
Tutorial zur Cloud-Server-Nutzung
 js-String in Array umwandeln
js-String in Array umwandeln
 So ersetzen Sie alle PPT-Hintergründe
So ersetzen Sie alle PPT-Hintergründe
 Wie funktioniert ein Schalter?
Wie funktioniert ein Schalter?
 So laden Sie den Razer-Maustreiber herunter
So laden Sie den Razer-Maustreiber herunter
 So öffnen Sie eine ISO-Datei
So öffnen Sie eine ISO-Datei
 Welche Bildbearbeitungssoftware gibt es?
Welche Bildbearbeitungssoftware gibt es?
 Empfohlene Lernreihenfolge für C++ und Python
Empfohlene Lernreihenfolge für C++ und Python




