Ein paar Codezeilen stabilisieren UNet! Die Sun Yat-sen University und andere schlugen das ScaleLong-Diffusionsmodell vor: von der Infragestellung der Skalierung zur Skalierung

In der Standard-UNet-Struktur beträgt der Skalierungskoeffizient 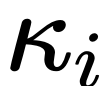auf der Long-Skip-Verbindung im Allgemeinen 1.

In einigen bekannten Diffusionsmodellarbeiten wie Imagen, Score-basiertes generatives Modell und SR3 usw. haben sie jedoch alle 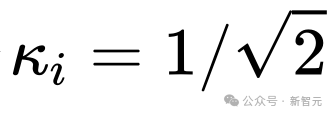festgelegt und festgestellt, dass solche Einstellungen das Diffusionstraining effektiv beschleunigen können Modelle.

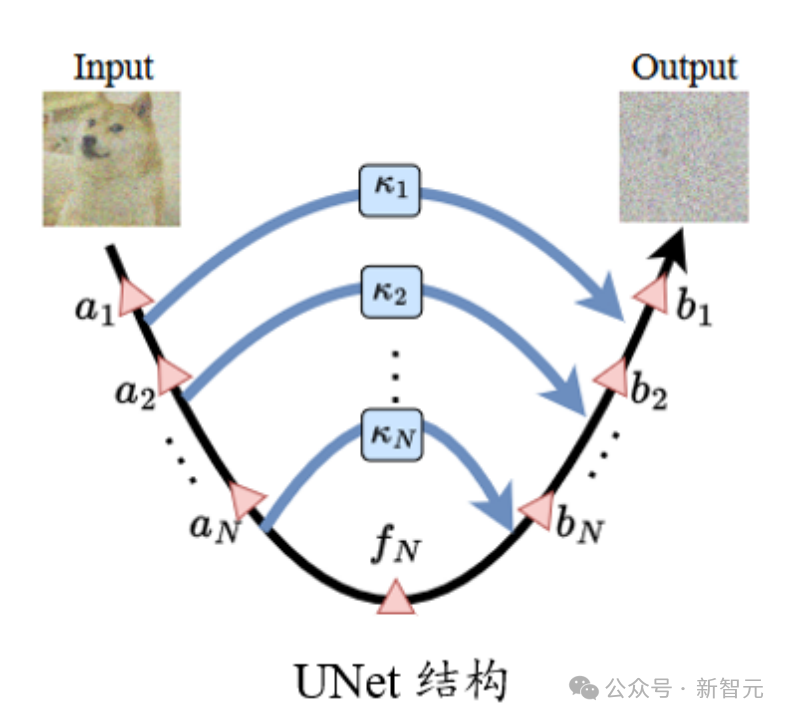
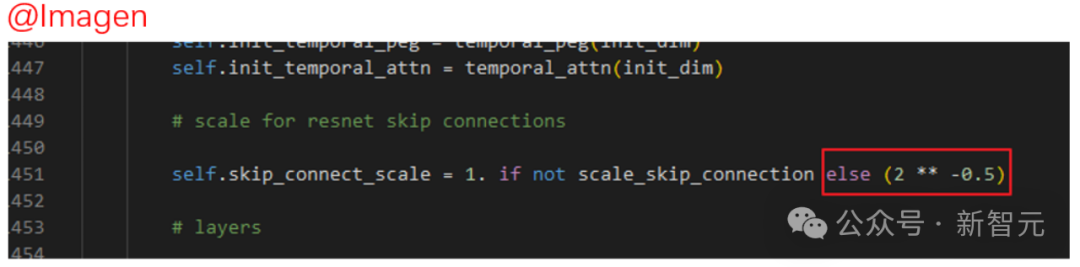
Skalierung in Frage stellenIm Originalpapier gibt es jedoch keine spezifische Analyse des Skalierungsvorgangs der Sprungverbindung in Imagen und anderen Modellen, es wird jedoch gesagt, dass diese Einstellung zur Beschleunigung beiträgt das Training des Diffusionsmodells.

Zuallererst macht uns diese Art der empirischen Darstellung unklar, welche Rolle dieses Setting spielt?

Außerdem wissen wir nicht, ob wir nur 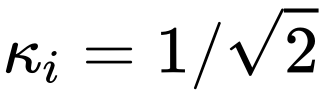festlegen können oder ob wir andere Konstanten verwenden können?

Sind die „Status“ von Skip-Verbindungen an verschiedenen Standorten gleich? Warum dieselbe Konstante verwenden?

Der Autor hat viele Fragezeichen dazu ...

Bilder

Skalierung verstehen

Im Allgemeinen ist UNet im Vergleich zu ResNet- und Transformer-Strukturen in der tatsächlichen Verwendung nicht „tief“. Da es nicht tief ist, ist es weniger anfällig für Optimierungsprobleme wie verschwindende Gradienten, die in anderen „tiefen“ neuronalen Netzwerkstrukturen häufig auftreten.

Darüber hinaus werden aufgrund der Besonderheit der UNet-Struktur flache Features durch lange Sprungverbindungen mit tiefen Standorten verbunden, wodurch Probleme wie das Verschwinden des Gradienten weiter vermieden werden.

Denken Sie andersherum: Wenn eine solche Struktur nicht beachtet wird, führt dies dann zu Problemen wie übermäßigen Steigungen und Parameter-(Merkmals-)Schwankungen aufgrund von Aktualisierungen?

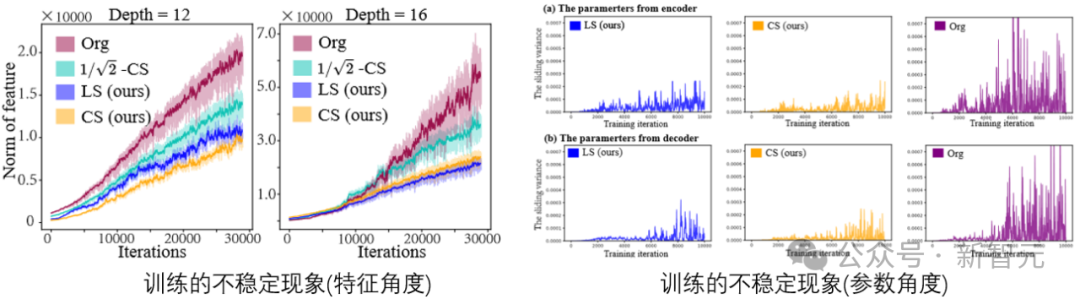Bilder

Durch die Visualisierung der Merkmale und Parameter der Diffusionsmodellaufgabe während des Trainingsprozesses kann festgestellt werden, dass tatsächlich Instabilität vorliegt.

Die Instabilität von Parametern (Features) wirkt sich auf den Gradienten aus, was wiederum Auswirkungen auf Parameteraktualisierungen hat. Letztendlich besteht bei diesem Prozess ein höheres Risiko unerwünschter Beeinträchtigungen der Leistung. Deshalb müssen wir Wege finden, diese Instabilität zu kontrollieren.

Ferner für das Diffusionsmodell. Die Eingabe von UNet ist ein verrauschtes Bild. Wenn das Modell das zusätzliche Rauschen genau vorhersagen soll, erfordert dies, dass das Modell eine hohe Robustheit gegenüber der Eingabe gegenüber zusätzlichen Störungen aufweist.

Papier: https://arxiv.org/abs/2310.13545

Code: https://github.com/sail-sg/ScaleLong

Forscher haben die oben genannten Probleme gefunden, die in Long zu finden sind Verbindung überspringen Die Skalierung wird auf dem System zur einheitlichen Schadensbegrenzung durchgeführt.

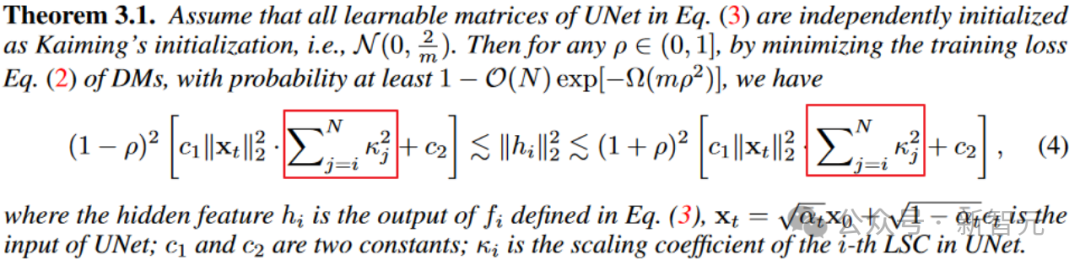
Aus Satz 3.1 steht der Schwingungsbereich des Merkmals der mittleren Schicht (die Breite der Ober- und Untergrenze) in direktem Zusammenhang mit der Summe der Quadrate des Skalierungskoeffizienten. Geeignete Skalierungskoeffizienten tragen dazu bei, die Instabilität von Merkmalen zu verringern.

Allerdings ist zu beachten, dass der Schock tatsächlich optimal gemildert wird, wenn der Skalierungskoeffizient direkt auf 0 gesetzt wird. (Manueller Hundekopf)

Aber wenn UNet zu einer Situation ohne Sprünge degradiert, ist das Instabilitätsproblem gelöst, aber auch die Darstellungsfähigkeit geht verloren. Dies ist ein Kompromiss zwischen Modellstabilität und Darstellungsfähigkeiten.

Bilder

Ähnlich aus der Perspektive des Parametergradienten. Satz 3.3 zeigt auch, dass der Skalierungskoeffizient die Größe des Gradienten steuert.

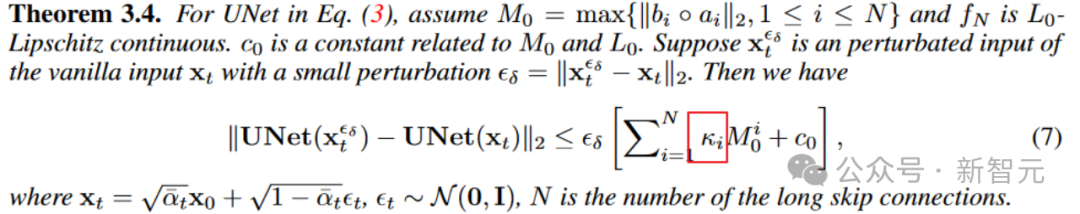Bild

Darüber hinaus zeigt Satz 3.4 auch, dass die Skalierung der Long-Skip-Verbindung auch die robuste Obergrenze des Modells gegenüber Eingangsstörungen beeinflussen und die Stabilität des Diffusionsmodells gegenüber Eingangsstörungen verbessern kann.

Become Scaling

Durch die obige Analyse verstehen wir, wie wichtig die Skalierung auf Long-Skip-Verbindungen für ein stabiles Modelltraining ist. 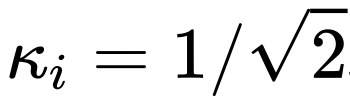gilt auch für die obige Analyse.

Als nächstes analysieren wir, welche Art von Skalierung eine bessere Leistung erzielen kann. Schließlich kann die obige Analyse nur zeigen, dass die Skalierung gut ist, aber sie kann nicht bestimmen, welche Art von Skalierung die beste oder bessere ist.

Eine einfache Möglichkeit besteht darin, ein lernbares Modul für eine lange Sprungverbindung einzuführen, um die Skalierung adaptiv anzupassen. Diese Methode wird als Learnable Scaling (LS)-Methode bezeichnet. Wir übernehmen eine SENet-ähnliche Struktur, die wie folgt aussieht (die hier betrachtete U-ViT-Struktur ist sehr gut organisiert!) Training von Diffusionsmodellen! Darüber hinaus versuchen wir, die in LS gelernten Koeffizienten zu visualisieren.

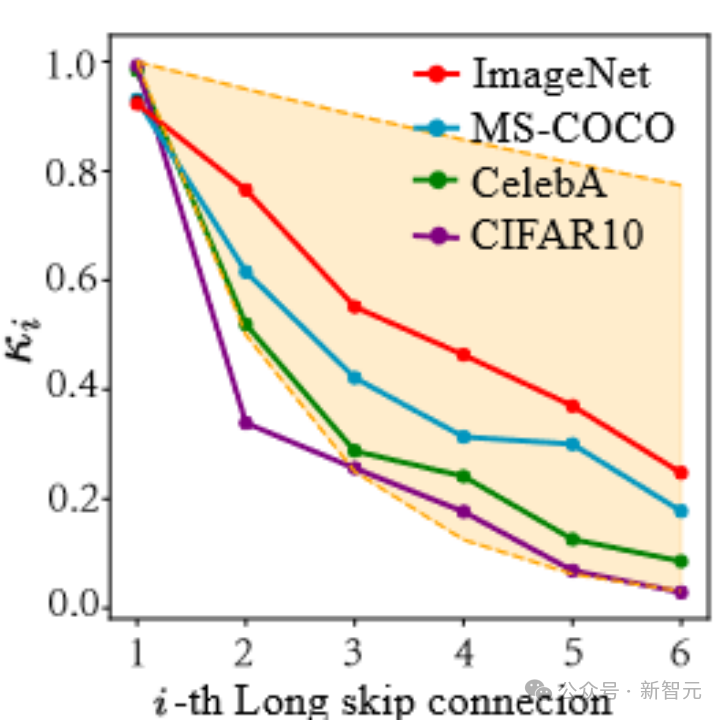
Wie in der folgenden Abbildung gezeigt, werden wir feststellen, dass diese Koeffizienten einen exponentiellen Abwärtstrend aufweisen (beachten Sie, dass sich die erste lange Sprungverbindung hier auf die Verbindung bezieht, die das erste und letzte Ende von UNet verbindet), und der erste Koeffizient liegt fast nahe beieinander zu 1. Das Phänomen ist auch erstaunlich!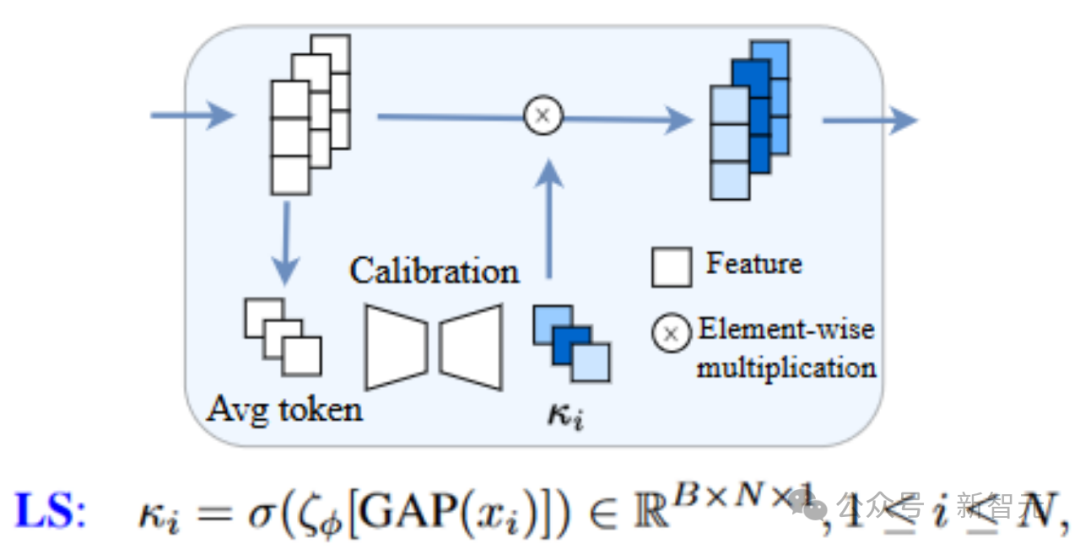

Bild

Basierend auf dieser Beobachtungsreihe (weitere Einzelheiten finden Sie im Artikel) haben wir außerdem die Constant Scaling (CS)-Methode vorgeschlagen, die keine lernbaren Parameter erfordert:

Die CS-Strategie erfordert keine zusätzlichen Parameter wie die ursprüngliche Skalierungsoperation mit

, sodass fast kein zusätzlicher Rechenaufwand entsteht.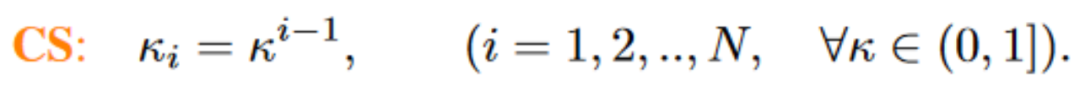

Obwohl CS im Stalltraining die meiste Zeit nicht so gut abschneidet wie LS, ist es für die bestehenden

Strategien dennoch einen Versuch wert.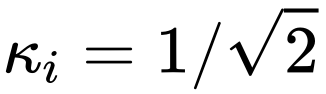

Die oben genannten Implementierungen von CS und LS sind sehr einfach und erfordern nur wenige Codezeilen. Für jede (hua)-Formel (li) und jede (hu)-artige (shao) UNet-Struktur müssen die Merkmalsabmessungen möglicherweise angepasst werden. (Manueller Hundekopf +1)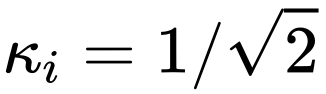

Kürzlich haben auch einige Folgearbeiten wie FreeU, SCEdit und andere gezeigt, wie wichtig die Skalierung bei Skip-Verbindungen ist. Jeder ist herzlich eingeladen, es zu versuchen und zu fördern.

Das obige ist der detaillierte Inhalt vonEin paar Codezeilen stabilisieren UNet! Die Sun Yat-sen University und andere schlugen das ScaleLong-Diffusionsmodell vor: von der Infragestellung der Skalierung zur Skalierung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!