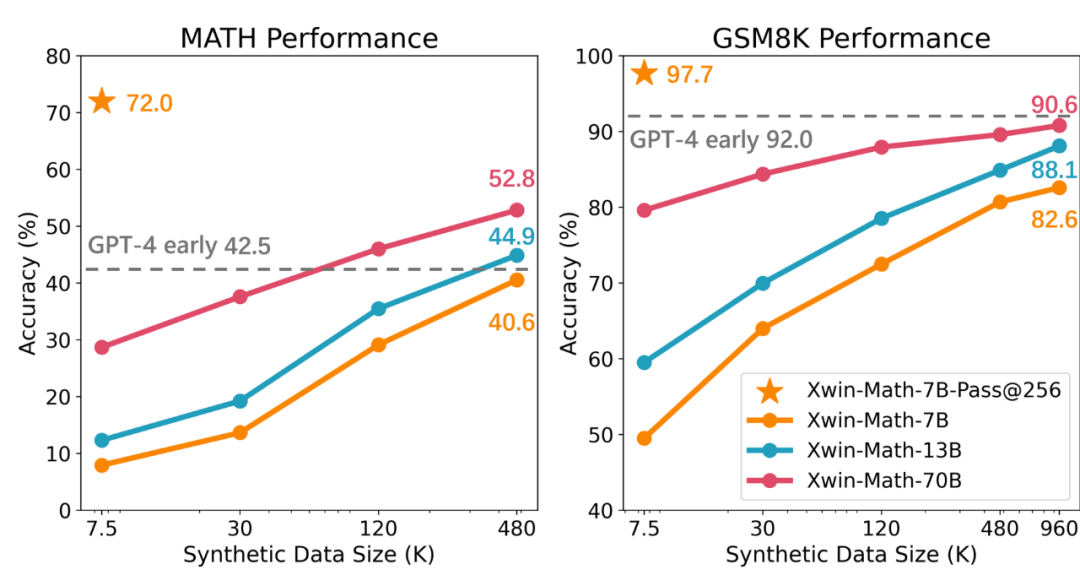
Die Obergrenze der mathematischen Fähigkeiten von LLaMA-2-7B hat 97,7 % erreicht? Xwin-Math erschließt Potenziale mit synthetischen Daten

Synthetische Daten erschließen weiterhin das mathematische Denkpotenzial großer Modelle!

Mathematische Problemlösungsfähigkeit gilt seit jeher als wichtiger Indikator für den Intelligenzgrad von Sprachmodellen. Normalerweise haben nur sehr große Modelle oder Modelle, die ein umfassendes mathematisches Vortraining durchlaufen haben, eine Chance, bei mathematischen Problemen gute Ergebnisse zu erzielen.

Kürzlich hat eine vom Swin-Transformer-Team erstellte und gemeinsam von Wissenschaftlern der Xi'an Jiaotong University, der University of Science and Technology of China, der Tsinghua University und Microsoft Research Asia erstellte Forschungsarbeit Xwin diese Wahrnehmung untergraben und enthüllt Das Sprachmodell im Maßstab 7B (d. h. 7 Milliarden Parameter) (LLaMA-2-7B) hat im Rahmen einer allgemeinen Vorschulung großes Potenzial bei der Lösung mathematischer Probleme gezeigt und kann überwachte Feinabstimmungsmethoden auf der Grundlage synthetischer Daten verwenden, um das Modell immer weiter zu verbessern Perfekt. Stetige Förderung der mathematischen Fähigkeiten.

Diese Studie wurde auf arXiv mit dem Titel „Common 7B Language Models Again Possess Strong Math Capabilities“ veröffentlicht.

• Papier-Link: https://arxiv.org/pdf/2403.04706.pdf
• Code-Link: https://github.com/Xwin-LM/Xwin-LM

Das Forschungsteam verwendete zunächst nur 7,5K-Daten zur Feinabstimmung der LLaMA-2-7B-Modellanweisungen und bewertete dann die Leistung des Modells in GSM8K und MATH. Experimentelle Ergebnisse zeigen, dass bei Auswahl der besten Antwort aus 256 generierten Antworten für jede Frage im Testsatz die Testgenauigkeit bis zu 97,7 % bzw. 72,0 % betragen kann. Dieses Ergebnis zeigt, dass selbst bei allgemeinem Vortraining das 7B-Niveau erreicht wird Die Entdeckung, dass selbst kleine Modelle das Potenzial haben, qualitativ hochwertige Antworten zu generieren, stellt die bisherige Ansicht in Frage, dass das Potenzial für leistungsstarkes mathematisches Denken nicht auf große und mathematisch verwandte vorab trainierte Modelle beschränkt ist.

Die Forschung weist jedoch auch darauf hin, dass das Hauptproblem aktueller Sprachmodelle trotz ihres starken mathematischen Denkvermögens darin besteht, dass es schwierig ist, ihre inhärenten mathematischen Fähigkeiten konsequent zu fördern. Wenn beispielsweise im vorherigen Experiment nur eine generierte Antwort pro Frage berücksichtigt wurde, würde die Genauigkeit der GSM8K- und MATH-Benchmarks auf 49,5 % bzw. 7,9 % sinken. Dies spiegelt die Instabilität der mathematischen Fähigkeiten des Modells wider. Um dieses Problem zu lösen, übernahm das Forschungsteam die Methode der Erweiterung des überwachten Feinabstimmungsdatensatzes (SFT) und stellte fest, dass mit der Zunahme der SFT-Daten die Zuverlässigkeit des Modells bei der Generierung korrekter Antworten erheblich verbessert wurde.

In der Studie wurde auch erwähnt, dass durch die Verwendung synthetischer Daten der SFT-Datensatz effektiv erweitert werden kann und diese Methode fast so effektiv ist wie echte Daten. Das Forschungsteam nutzte die GPT-4 Turbo API, um synthetische mathematische Fragen und Problemlösungsprozesse zu generieren, und stellte die Qualität der Fragen durch einfache Verifizierungsaufforderungswörter sicher. Mit dieser Methode konnte das Team den SFT-Datensatz erfolgreich von 7,5.000 auf etwa eine Million Samples erweitern und so ein nahezu perfektes Skalierungsgesetz erreichen. Das resultierende Xwin-Math-7B-Modell erreichte eine Genauigkeit von 82,6 % bzw. 40,6 % auf GSM8K bzw. MATH und übertraf damit frühere SOTA-Modelle deutlich und sogar einige 70B-Modelle, wodurch eine sprunghafte Verbesserung erzielt wurde. Das Xwin-Math-70B-Modell erzielte im MATH-Bewertungssatz ein Ergebnis von 52,8 % und übertraf damit die frühe Version von GPT-4 deutlich. Dies ist das erste Mal, dass die auf der LLaMA-Reihe von Basismodellen basierende Forschung GPT-4 in MATH übertrifft.

Die Forscher haben auch die Bewertungsindikatoren Pass@N und PassRatio@N definiert, um zu bewerten, ob das Modell die richtige Antwort ausgeben kann (was auf die potenzielle mathematische Fähigkeit des Modells hinweist) und wie hoch der Anteil der richtigen Antworten unter den N ist Ergebnisse des Modells (die die Stabilität der mathematischen Fähigkeiten des Modells anzeigen). Wenn die Menge an SFT-Daten klein ist, ist der Pass@256 des Modells bereits sehr hoch. Nach einer weiteren Erweiterung der SFT-Datenskala erhöht sich der Pass@256 des Modells nur sehr wenig, während das PassRatio@256 deutlich zunimmt. Dies zeigt, dass eine überwachte Feinabstimmung auf der Grundlage synthetischer Daten eine wirksame Möglichkeit ist, die Stabilität der mathematischen Fähigkeiten des Modells zu verbessern.

Darüber hinaus liefert die Studie Einblicke in das Skalierungsverhalten bei verschiedenen Argumentationskomplexitäten und Fehlertypen. Wenn beispielsweise die Größe des SFT-Datensatzes zunimmt, folgt die Genauigkeit des Modells bei der Lösung mathematischer Probleme einer Potenzgesetzbeziehung mit der Anzahl der Inferenzschritte. Durch die Erhöhung des Anteils langer Inferenzschritte in den Trainingsbeispielen kann die Genauigkeit des Modells bei der Lösung schwieriger Probleme deutlich verbessert werden. Gleichzeitig stellte die Studie auch fest, dass Berechnungsfehler leichter zu mildern sind als Argumentationsfehler.

In der Mathematikprüfung der ungarischen Oberstufe, die die Verallgemeinerungsfähigkeit des Modells für mathematisches Denken zum Ausdruck bringt, erreichte Xwin-Math ebenfalls 65 %, nur nach GPT-4 den zweiten Platz. Dies zeigt, dass die Art und Weise, wie die Daten in der Studie synthetisiert wurden, nicht wesentlich an den Bewertungssatz angepasst war und eine gute Generalisierungsfähigkeit zeigte.

Diese Studie demonstriert nicht nur die Wirksamkeit synthetischer Daten bei der Erweiterung von SFT-Daten, sondern bietet auch eine neue Perspektive auf die Erforschung großer Sprachmodelle im Bereich der mathematischen Denkfähigkeiten. Das Forschungsteam erklärte, dass seine Arbeit den Grundstein für zukünftige Erforschung und Fortschritte auf diesem Gebiet gelegt habe, und freue sich darauf, künstliche Intelligenz zu fördern, um größere Durchbrüche bei der Lösung mathematischer Probleme zu erzielen. Angesichts der kontinuierlichen Weiterentwicklung der Technologie der künstlichen Intelligenz haben wir Grund zu der Annahme, dass KI im Bereich der Mathematik noch bessere Leistungen erbringen und Menschen mehr Hilfe bei der Lösung komplexer mathematischer Probleme bieten wird.

Der Artikel behandelt auch die Ergebnisse von Ablationsexperimenten und andere Bewertungsindikatoren der Datensynthesemethode. Einzelheiten finden Sie im vollständigen Text.

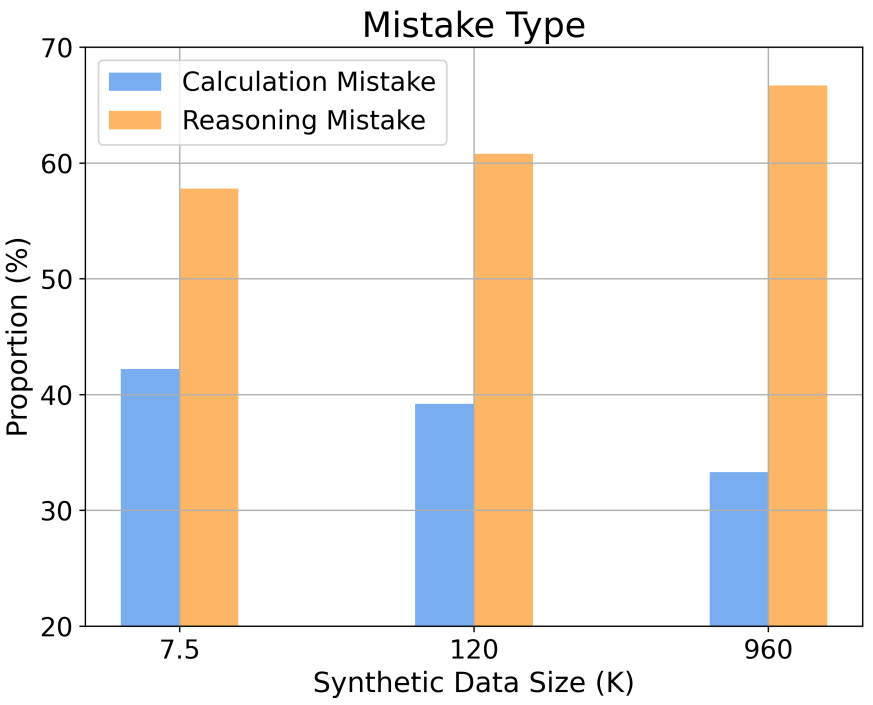
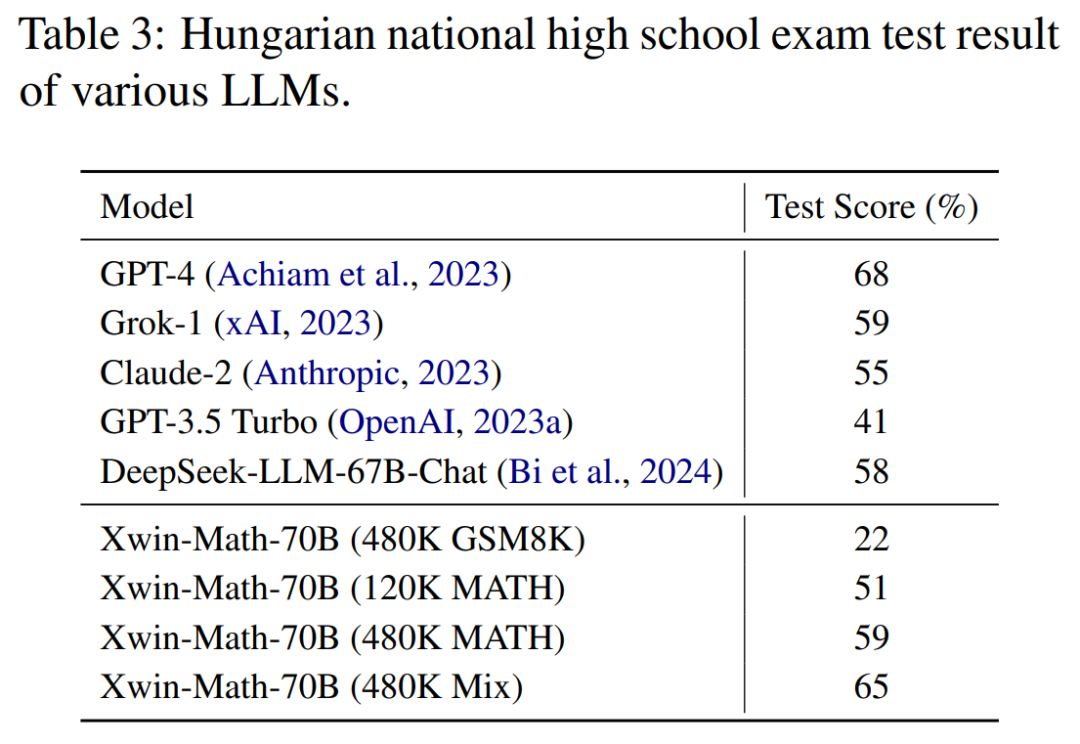
Das obige ist der detaillierte Inhalt vonDie Obergrenze der mathematischen Fähigkeiten von LLaMA-2-7B hat 97,7 % erreicht? Xwin-Math erschließt Potenziale mit synthetischen Daten. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!