 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 CUDAs universelle Matrixmultiplikation: vom Einstieg bis zur Kompetenz!
CUDAs universelle Matrixmultiplikation: vom Einstieg bis zur Kompetenz!
CUDAs universelle Matrixmultiplikation: vom Einstieg bis zur Kompetenz!
Die allgemeine Matrixmultiplikation (GEMM) ist ein wichtiger Bestandteil vieler Anwendungen und Algorithmen und auch einer der wichtigen Indikatoren zur Bewertung der Leistung der Computerhardware. Eingehende Forschung und Optimierung der Implementierung von GEMM können uns helfen, Hochleistungsrechnen und die Beziehung zwischen Software- und Hardwaresystemen besser zu verstehen. In der Informatik kann eine effektive Optimierung von GEMM die Rechengeschwindigkeit erhöhen und Ressourcen einsparen, was für die Verbesserung der Gesamtleistung eines Computersystems von entscheidender Bedeutung ist. Ein tiefgreifendes Verständnis des Funktionsprinzips und der Optimierungsmethode von GEMM wird uns helfen, das Potenzial moderner Computerhardware besser zu nutzen und effizientere Lösungen für verschiedene komplexe Computeraufgaben bereitzustellen. Durch die Optimierung und Verbesserung der Leistung von GEMM können wir Folgendes hinzufügen:
1. Grundlegende Merkmale von GEMM
1.1 GEMM-Berechnungsprozess und Komplexität
GEMM ist definiert als:
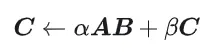

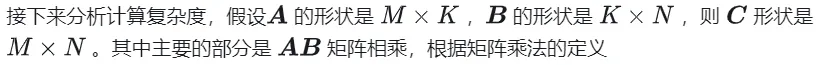
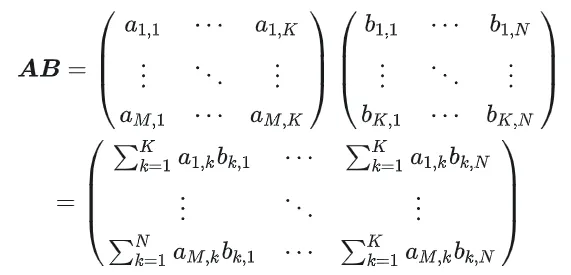


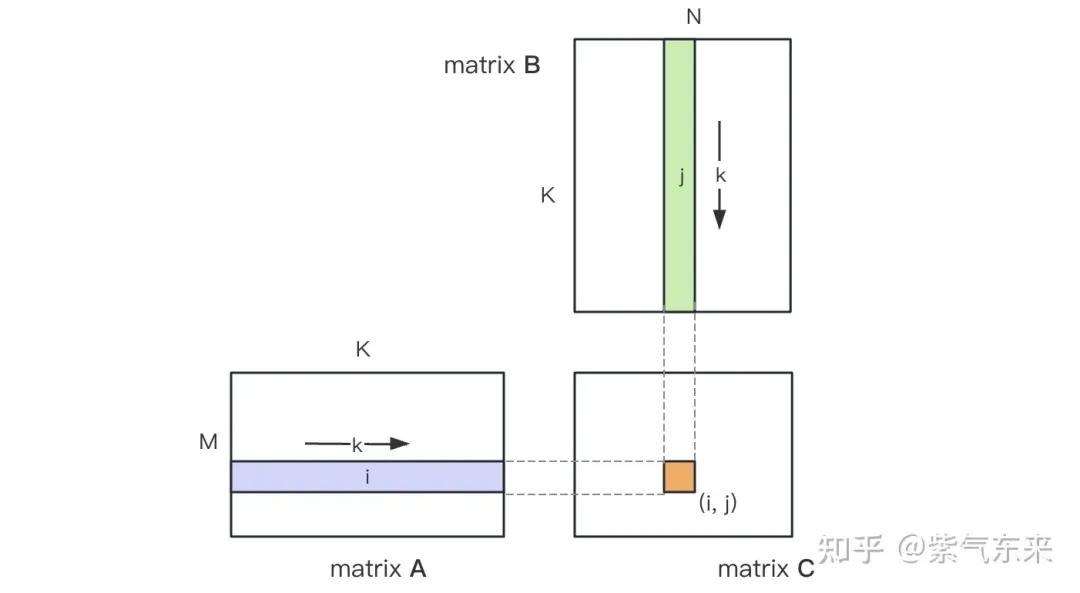
Rechendiagramm der Matrixmultiplikation
1.2 Einfache Implementierung und Prozessanalyse
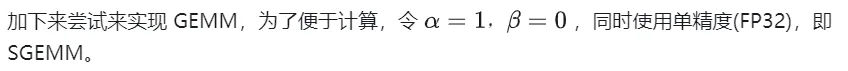
Das Folgende ist der auf der CPU gemäß der ursprünglichen Definition implementierte Code, der als Steuerung verwendet wird für die Genauigkeit
#define OFFSET(row, col, ld) ((row) * (ld) + (col))void cpuSgemm(float *a, float *b, float *c, const int M, const int N, const int K) {for (int m = 0; m Im Folgenden wird CUDA zur Implementierung von Kernal verwendet, der einfachsten Matrixmultiplikation. Insgesamt werden M * N Threads verwendet, um die gesamte Matrixmultiplikation abzuschließen. Jeder Thread ist für die Berechnung eines Elements in der Matrix C verantwortlich und muss K-fache Multiplikationen und Akkumulationen durchführen. Die Matrizen A, B und C werden alle im globalen Speicher gespeichert (bestimmt durch den Modifikator __global__ Siehe sgemm_naive.cu für den vollständigen Code).
__global__ void naiveSgemm(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,const int M, const int N, const int K) {int n = blockIdx.x * blockDim.x + threadIdx.x;int m = blockIdx.y * blockDim.y + threadIdx.y;if (m Die Kompilierung ist abgeschlossen und die Ergebnisse der Ausführung auf Tesla V100-PCIE-32GB lauten wie folgt: Laut V100-Whitepaper beträgt die maximale Rechenleistung von FP32 15,7 TFLOPS, also die Rechenleistungsauslastung Methode beträgt nur 11,5 %.
M N K =128128 1024, Time = 0.00010083 0.00010260 0.00010874 s, AVG Performance = 304.5951 GflopsM N K =192192 1024, Time = 0.00010173 0.00010198 0.00010253 s, AVG Performance = 689.4680 GflopsM N K =256256 1024, Time = 0.00010266 0.00010318 0.00010384 s, AVG Performance =1211.4281 GflopsM N K =384384 1024, Time = 0.00019475 0.00019535 0.00019594 s, AVG Performance =1439.7206 GflopsM N K =512512 1024, Time = 0.00037693 0.00037794 0.00037850 s, AVG Performance =1322.9753 GflopsM N K =768768 1024, Time = 0.00075238 0.00075558 0.00075776 s, AVG Performance =1488.9271 GflopsM N K = 1024 1024 1024, Time = 0.00121562 0.00121669 0.00121789 s, AVG Performance =1643.8068 GflopsM N K = 1536 1536 1024, Time = 0.00273072 0.00275611 0.00280208 s, AVG Performance =1632.7386 GflopsM N K = 2048 2048 1024, Time = 0.00487622 0.00488028 0.00488614 s, AVG Performance =1639.2518 GflopsM N K = 3072 3072 1024, Time = 0.01001603 0.01071136 0.01099990 s, AVG Performance =1680.4589 GflopsM N K = 4096 4096 1024, Time = 0.01771046 0.01792170 0.01803462 s, AVG Performance =1785.5450 GflopsM N K = 6144 6144 1024, Time = 0.03988969 0.03993405 0.04000595 s, AVG Performance =1802.9724 GflopsM N K = 8192 8192 1024, Time = 0.07119219 0.07139694 0.07160816 s, AVG Performance =1792.7940 GflopsM N K =1228812288 1024, Time = 0.15978026 0.15993242 0.16043369 s, AVG Performance =1800.7606 GflopsM N K =1638416384 1024, Time = 0.28559187 0.28567238 0.28573316 s, AVG Performance =1792.2629 Gflops
Im Folgenden wird M=512, K=512, N=512 als Beispiel verwendet, um den Arbeitsablauf des obigen Berechnungsprozesses im Detail zu analysieren:
- Reservieren Sie im globalen Speicher Speicherplatz für die Matrizen A, B und C.
- Wegen der Matrix Die Berechnung jedes Elements in C ist unabhängig voneinander, sodass in der Parallelitätszuordnung jeder Thread der Berechnung eines Elements in Matrix C entspricht.
- Sowohl GridSize als auch BlockSize in der Ausführungskonfiguration haben x (Spaltenrichtung), y (Zeilenrichtung) zwei Dimensionen, darunter


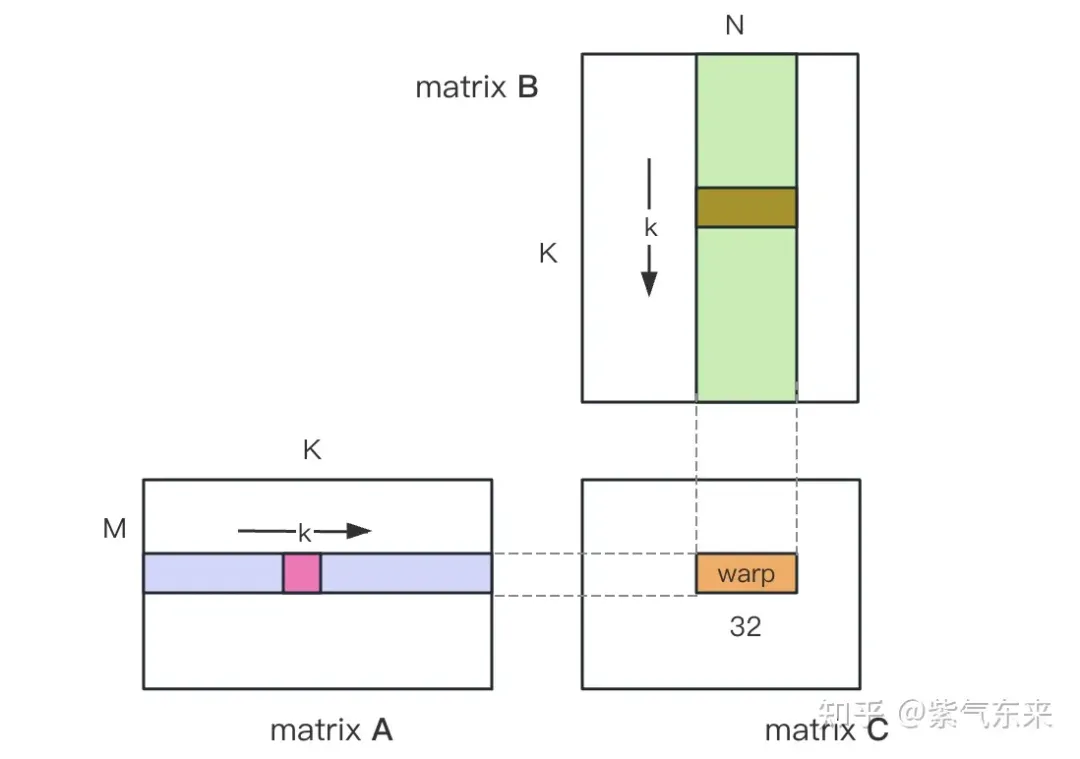


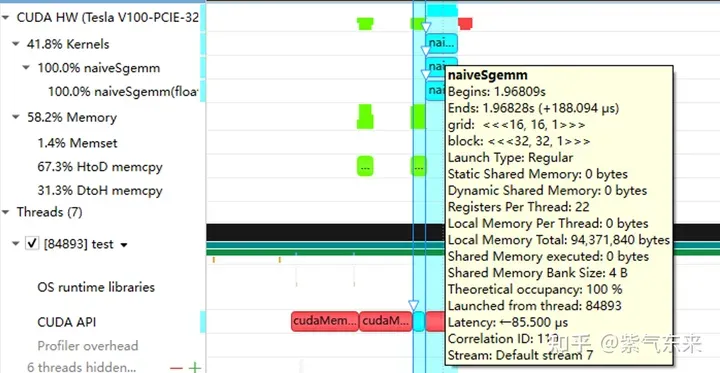
nsys zeichnet die naive Version der Profilerstellung auf
2. GEMM-Optimierungsexploration
Das Vorherige Der Artikel ist nur funktional, GEMM wurde implementiert, aber die Leistung ist weit von den Erwartungen entfernt. In diesem Abschnitt wird hauptsächlich die Optimierung der GEMM-Leistung untersucht.
2.1 Matrixpartitionierung mit Shared Memory
Die obige Berechnung erfordert zwei globale Speicherladungen, um eine Multiplikations- und Akkumulationsoperation abzuschließen. Das Berechnungsspeicherzugriffsverhältnis ist extrem niedrig und es gibt keine effektive Datenwiederverwendung. Daher kann Shared Memory verwendet werden, um wiederholte Speicherlesevorgänge zu reduzieren.
Teilen Sie zunächst die Matrix C in gleiche Blöcke mit der Größe BMxBN. Jeder Block wird durch einen Block berechnet, wobei jeder Thread für die Berechnung der TMxTN-Elemente in der Matrix C verantwortlich ist. Anschließend werden alle für die Berechnung erforderlichen Daten aus smem gelesen, wodurch ein Teil des wiederholten Speicherauslesens der A- und B-Matrizen entfällt. In Anbetracht der begrenzten Kapazität des gemeinsam genutzten Speichers können Blöcke der Größe BK jedes Mal in K-Dimensionen gelesen werden. Eine solche Schleife erfordert insgesamt K / BK-Zeiten, um die gesamte Matrixmultiplikationsoperation abzuschließen und das Ergebnis des Blocks zu erhalten. Der Prozess ist in der folgenden Abbildung dargestellt:
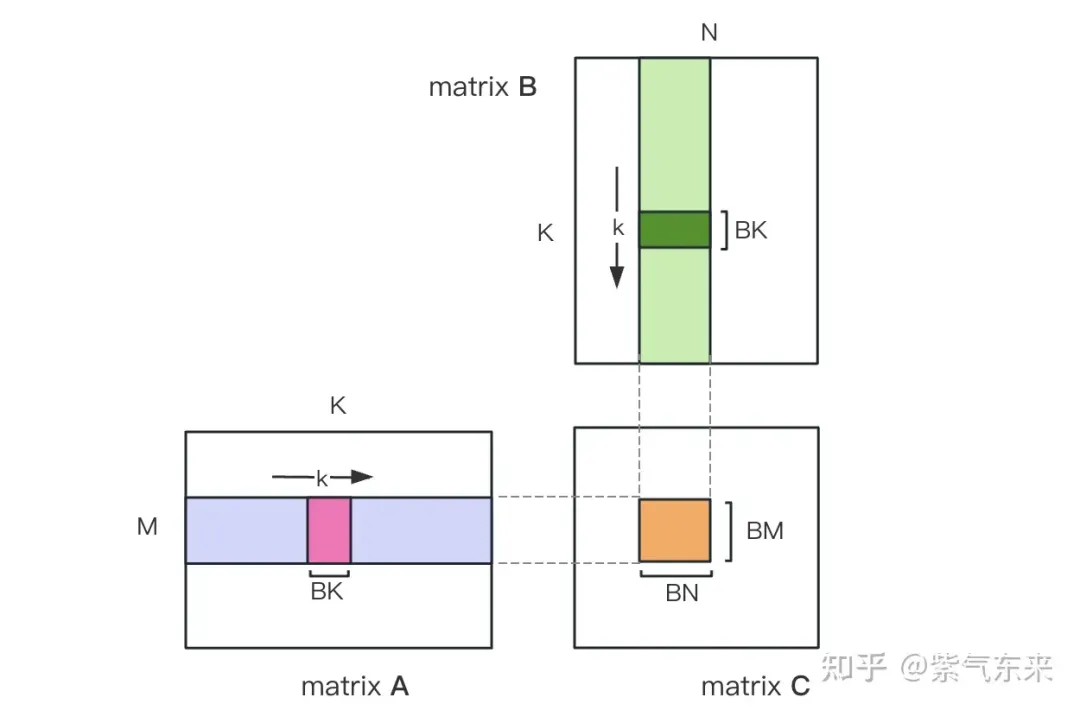
Nach der Optimierung mit Shared Memory können wir für jeden Block Folgendes erhalten:
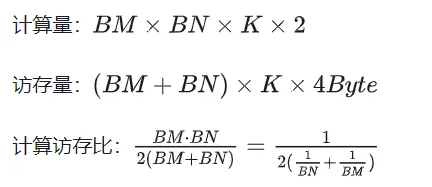
Aus der obigen Formel ist ersichtlich, dass je größer BM und BN sind, desto größer Je höher das Rechenspeicherzugriffsverhältnis, desto besser ist die Leistung. Aufgrund der begrenzten Shared-Memory-Kapazität (V100 1 SM ist nur 96 KB groß) muss ein Block jedoch BK * (BM + BN) * 4 Bytes belegen.
Die Werte von TM und TN sind auch durch zwei Aspekte begrenzt. Einerseits gibt es Einschränkungen hinsichtlich der Anzahl der Threads in einem Block 1024 überschreiten und nicht zu hoch sein, um zu verhindern, dass die Parallelität zwischen Blöcken beeinträchtigt wird. Ein Thread benötigt jedoch mindestens TM * TN-Register, um die Teilsumme zu speichern Matrix C und einige andere Register. Die Anzahl aller Register darf 256 nicht überschreiten und darf nicht zu hoch sein, um eine Beeinträchtigung der Anzahl gleichzeitiger Threads in SM zu verhindern.
Wählen Sie abschließend BM = BN = 128, BK = 8, TM = TN = 8, dann beträgt das berechnete Speicherzugriffsverhältnis 32. Gemäß der theoretischen Rechenleistung des V100 von 15,7 TFLOPS können wir 15,7 TFLOPS/32 = 490 GB/s erreichen. Da die gemessene HBM-Bandbreite 763 GB/s beträgt, ist ersichtlich, dass die Bandbreite die Rechenleistung dabei nicht mehr einschränkt Zeit.
Basierend auf der obigen Analyse ist der Kernel-Funktionsimplementierungsprozess wie folgt. Den vollständigen Code finden Sie unter sgemm_v1.cu. Die Hauptschritte umfassen:
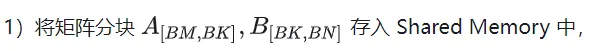

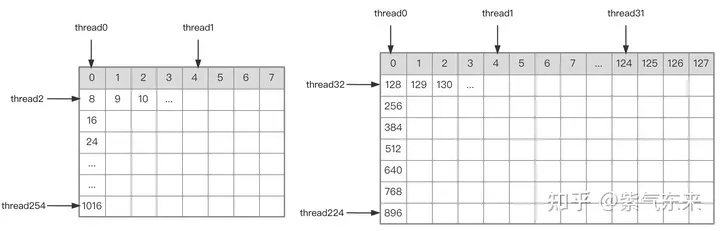
A B Thread-Indexbeziehung der Matrixpartitionierung
确定好单个block的执行过程,接下来需要确定多block处理的不同分块在Global Memory中的对应关系,仍然以A为例进行说明。由于分块沿着行的方向移动,那么首先需要确定行号,根据 Grid 的二维全局线性索引关系,by * BM 表示该分块的起始行号,同时我们已知load_a_smem_m 为分块内部的行号,因此全局的行号为load_a_gmem_m = by * BM + load_a_smem_m 。由于分块沿着行的方向移动,因此列是变化的,需要在循环内部计算,同样也是先计算起始列号bk * BK 加速分块内部列号load_a_smem_k 得到 load_a_gmem_k = bk * BK + load_a_smem_k ,由此我们便可以确定了分块在原始数据中的位置OFFSET(load_a_gmem_m, load_a_gmem_k, K) 。同理可分析矩阵分块 的情况,不再赘述。

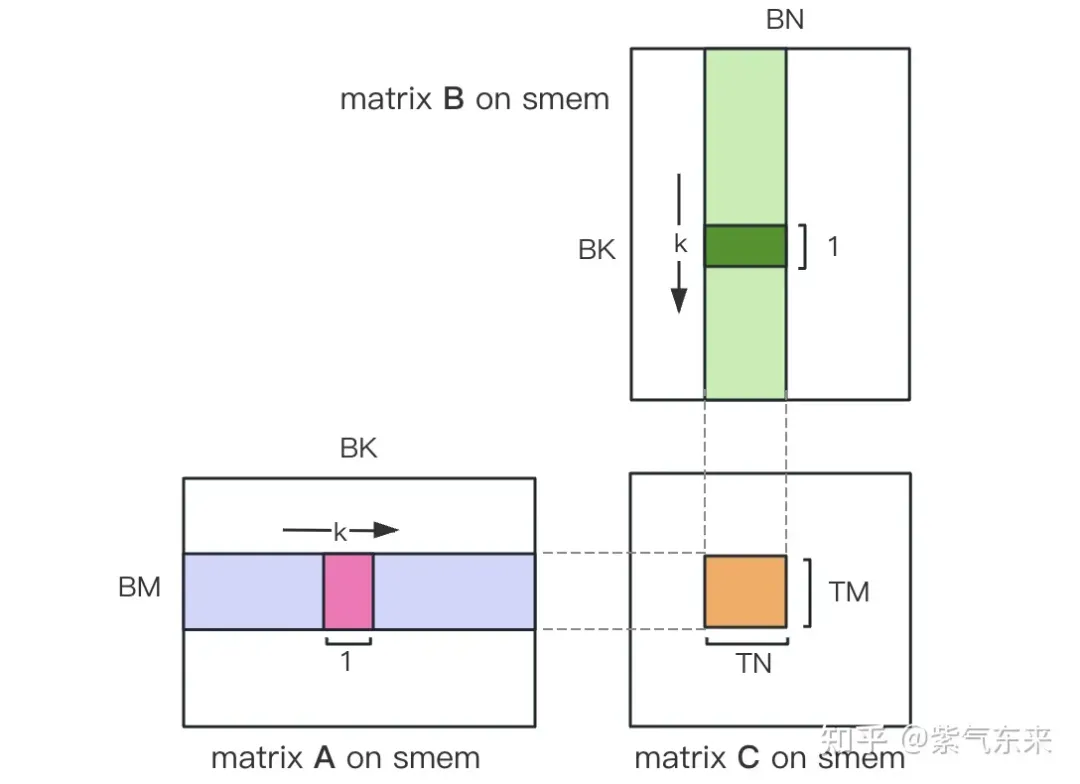
计算完后,还需要将其存入 Global Memory 中,这就需要计算其在 Global Memory 中的对应关系。由于存在更小的分块,则行和列均由3部分构成:全局行号store_c_gmem_m 等于大分块的起始行号by * BM+小分块的起始行号ty * TM+小分块内部的相对行号 i 。列同理。
__global__ void sgemm_V1(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,const int M, const int N, const int K) {const int BM = 128;const int BN = 128;const int BK = 8;const int TM = 8;const int TN = 8;const int bx = blockIdx.x;const int by = blockIdx.y;const int tx = threadIdx.x;const int ty = threadIdx.y;const int tid = ty * blockDim.x + tx;__shared__ float s_a[BM][BK];__shared__ float s_b[BK][BN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;// tid/2, row of s_aint load_a_smem_k = (tid & 1) > 5; // tid/32, row of s_bint load_b_smem_n = (tid & 31) 计算结果如下,性能达到了理论峰值性能的51.7%:
M N K =128128 1024, Time = 0.00031578 0.00031727 0.00032288 s, AVG Performance =98.4974 GflopsM N K =192192 1024, Time = 0.00031638 0.00031720 0.00031754 s, AVG Performance = 221.6661 GflopsM N K =256256 1024, Time = 0.00031488 0.00031532 0.00031606 s, AVG Performance = 396.4287 GflopsM N K =384384 1024, Time = 0.00031686 0.00031814 0.00032080 s, AVG Performance = 884.0425 GflopsM N K =512512 1024, Time = 0.00031814 0.00032007 0.00032493 s, AVG Performance =1562.1563 GflopsM N K =768768 1024, Time = 0.00032397 0.00034419 0.00034848 s, AVG Performance =3268.5245 GflopsM N K = 1024 1024 1024, Time = 0.00034570 0.00034792 0.00035331 s, AVG Performance =5748.3952 GflopsM N K = 1536 1536 1024, Time = 0.00068797 0.00068983 0.00069094 s, AVG Performance =6523.3424 GflopsM N K = 2048 2048 1024, Time = 0.00136173 0.00136552 0.00136899 s, AVG Performance =5858.5604 GflopsM N K = 3072 3072 1024, Time = 0.00271910 0.00273115 0.00274006 s, AVG Performance =6590.6331 GflopsM N K = 4096 4096 1024, Time = 0.00443805 0.00445964 0.00446883 s, AVG Performance =7175.4698 GflopsM N K = 6144 6144 1024, Time = 0.00917891 0.00950608 0.00996963 s, AVG Performance =7574.0999 GflopsM N K = 8192 8192 1024, Time = 0.01628838 0.01645271 0.01660790 s, AVG Performance =7779.8733 GflopsM N K =1228812288 1024, Time = 0.03592557 0.03597434 0.03614323 s, AVG Performance =8005.7066 GflopsM N K =1638416384 1024, Time = 0.06304122 0.06306373 0.06309302 s, AVG Performance =8118.7715 Gflops
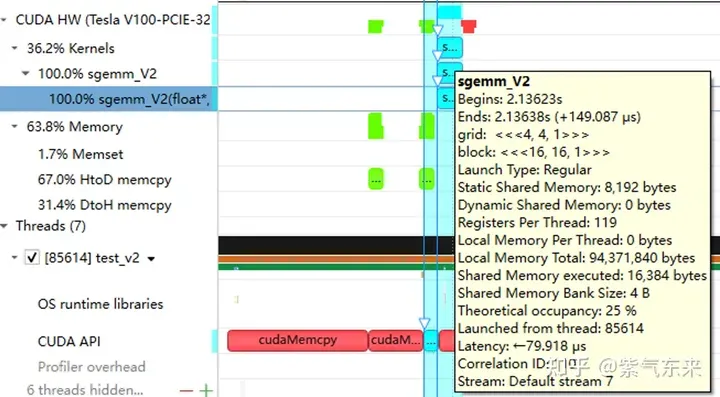
下面仍以M=512,K=512,N=512为例,分析一下结果。首先通过 profiling 可以看到 Shared Memory 占用为 8192 bytes,这与理论上(128+128)X8X4完全一致。
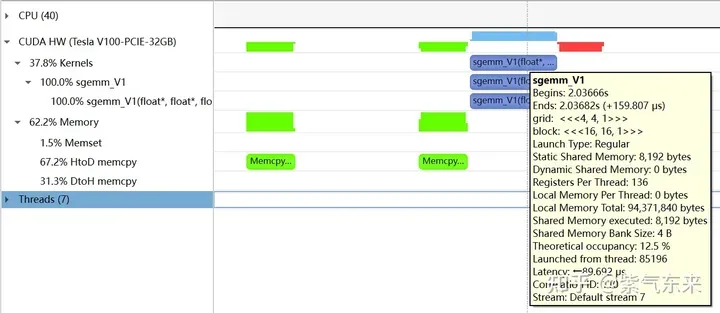 nsys 记录 的 V1 版本的 profiling
nsys 记录 的 V1 版本的 profiling
profiling 显示 Occupancy 为 12.5%,可以通过 cuda-calculator 加以印证,该例中 threads per block = 256, Registers per thread = 136, 由此可以计算得到每个SM中活跃的 warp 为8,而对于V100,每个SM中的 warp 总数为64,因此 Occupancy 为 8/64 = 12.5%。
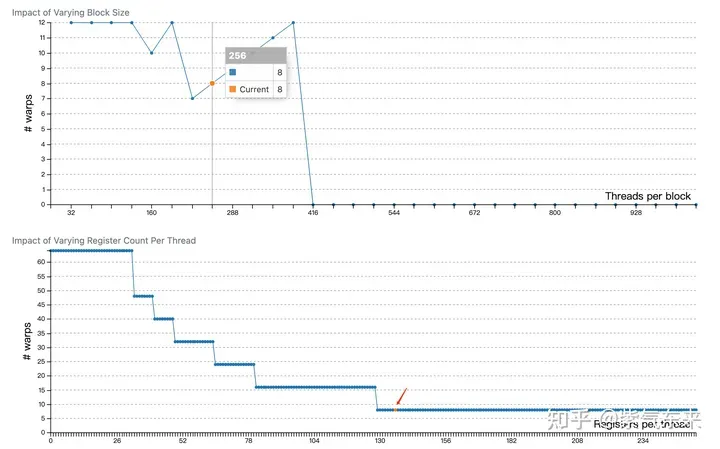
2.2 解决 Bank Conflict 问题
上节通过利用 Shared Memory 大幅提高了访存效率,进而提高了性能,本节将进一步优化 Shared Memory 的使用。
Shared Memory一共划分为32个Bank,每个Bank的宽度为4 Bytes,如果需要访问同一个Bank的多个数据,就会发生Bank Conflict。例如一个Warp的32个线程,如果访问的地址分别为0、4、8、...、124,就不会发生Bank Conflict,只占用Shared Memory一拍的时间;如果访问的地址为0、8、16、...、248,这样一来地址0和地址128对应的数据位于同一Bank、地址4和地址132对应的数据位于同一Bank,以此类推,那么就需要占用Shared Memory两拍的时间才能读出。
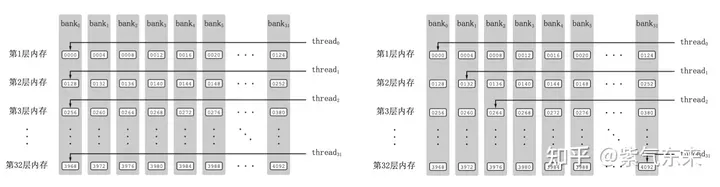
有 Bank Conflict VS 无 Bank Conflict
再看 V1 版本计算部分的三层循环,每次从Shared memory中取矩阵A的长度为TM的向量和矩阵B的长度为TN的向量,这两个向量做外积并累加到部分和中,一次外积共TM * TN次乘累加,一共需要循环BK次取数和外积。
接下来分析从Shared Memory load的过程中存在的Bank Conflict:
i) 取矩阵A需要取一个列向量,而矩阵A在Shared Memory中是按行存储的;
ii) 在TM = TN = 8的情况下,无论矩阵A还是矩阵B,从Shared Memory中取数时需要取连续的8个数,即便用LDS.128指令一条指令取四个数,也需要两条指令,由于一个线程的两条load指令的地址是连续的,那么同一个Warp不同线程的同一条load指令的访存地址就是被间隔开的,便存在着 Bank Conflict。
为了解决上述的两点Shared Memory的Bank Conflict,采用了一下两点优化:
i) 为矩阵A分配Shared Memory时形状分配为[BK][BM],即让矩阵A在Shared Memory中按列存储
ii) 将原本每个线程负责计算的TM * TN的矩阵C,划分为下图中这样的两块TM/2 * TN的矩阵C,由于TM/2=4,一条指令即可完成A的一块的load操作,两个load可同时进行。
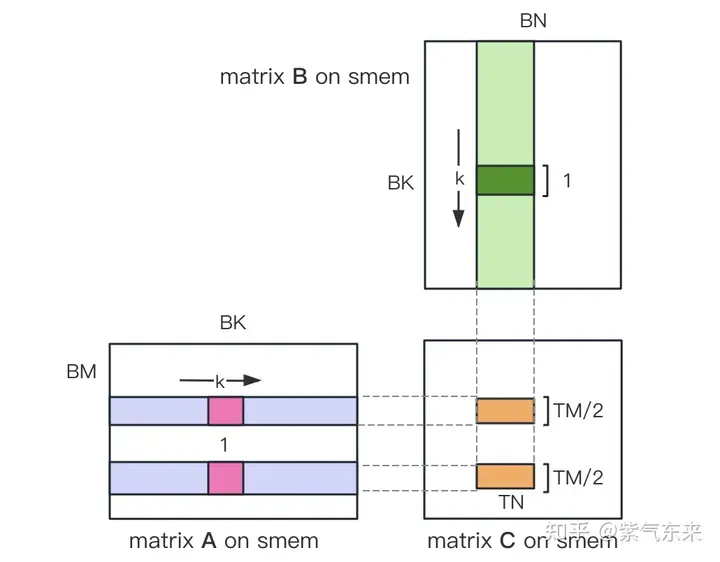
kernel 函数的核心部分实现如下,完整代码见 sgemm_v2.cu 。
__shared__ float s_a[BK][BM];__shared__ float s_b[BK][BN];float r_load_a[4];float r_load_b[4];float r_comp_a[TM];float r_comp_b[TN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) > 5;int load_b_smem_n = (tid & 31) 结果如下,相对未解决 Bank Conflict 版(V1) 性能提高了 14.4%,达到了理论峰值的74.3%。
M N K =128128 1024, Time = 0.00029699 0.00029918 0.00030989 s, AVG Performance = 104.4530 GflopsM N K =192192 1024, Time = 0.00029776 0.00029828 0.00029882 s, AVG Performance = 235.7252 GflopsM N K =256256 1024, Time = 0.00029485 0.00029530 0.00029619 s, AVG Performance = 423.2949 GflopsM N K =384384 1024, Time = 0.00029734 0.00029848 0.00030090 s, AVG Performance = 942.2843 GflopsM N K =512512 1024, Time = 0.00029853 0.00029945 0.00030070 s, AVG Performance =1669.7479 GflopsM N K =768768 1024, Time = 0.00030458 0.00032467 0.00032790 s, AVG Performance =3465.1038 GflopsM N K = 1024 1024 1024, Time = 0.00032406 0.00032494 0.00032621 s, AVG Performance =6155.0281 GflopsM N K = 1536 1536 1024, Time = 0.00047990 0.00048224 0.00048461 s, AVG Performance =9331.3912 GflopsM N K = 2048 2048 1024, Time = 0.00094426 0.00094636 0.00094992 s, AVG Performance =8453.4569 GflopsM N K = 3072 3072 1024, Time = 0.00187866 0.00188096 0.00188538 s, AVG Performance =9569.5816 GflopsM N K = 4096 4096 1024, Time = 0.00312589 0.00319050 0.00328147 s, AVG Performance = 10029.7885 GflopsM N K = 6144 6144 1024, Time = 0.00641280 0.00658940 0.00703498 s, AVG Performance = 10926.6372 GflopsM N K = 8192 8192 1024, Time = 0.01101130 0.01116194 0.01122950 s, AVG Performance = 11467.5446 GflopsM N K =1228812288 1024, Time = 0.02464854 0.02466705 0.02469344 s, AVG Performance = 11675.4946 GflopsM N K =1638416384 1024, Time = 0.04385955 0.04387468 0.04388355 s, AVG Performance = 11669.5995 Gflops
分析一下 profiling 可以看到 Static Shared Memory 仍然是使用了8192 Bytes,奇怪的的是,Shared Memory executed 却翻倍变成了 16384 Bytes(知友如果知道原因可以告诉我一下)。
2.3 流水并行化:Double Buffering
Double Buffering,即双缓冲,即通过增加buffer的方式,使得 访存-计算 的串行模式流水线化,以减少等待时间,提高计算效率,其原理如下图所示:
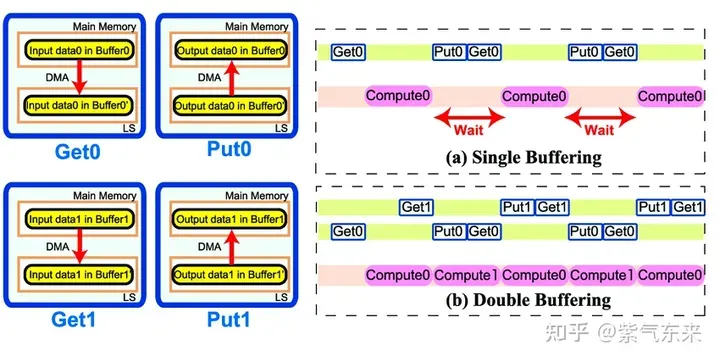
Single Buffering VS Double Buffering
具体到 GEMM 任务中来,就是需要两倍的Shared Memory,之前只需要BK * (BM + BN) * 4 Bytes的Shared Memory,采用Double Buffering之后需要2BK * (BM + BN) * 4 Bytes的Shared Memory,然后使其 pipeline 流动起来。
代码核心部分如下所示,完整代码参见 sgemm_v3.cu 。有以下几点需要注意:
1)主循环从bk = 1 开始,第一次数据加载在主循环之前,最后一次计算在主循环之后,这是pipeline 的特点决定的;
2)由于计算和下一次访存使用的Shared Memory不同,因此主循环中每次循环只需要一次__syncthreads()即可
3)由于GPU不能向CPU那样支持乱序执行,主循环中需要先将下一次循环计算需要的Gloabal Memory中的数据load 到寄存器,然后进行本次计算,之后再将load到寄存器中的数据写到Shared Memory,这样在LDG指令向Global Memory做load时,不会影响后续FFMA及其它运算指令的 launch 执行,也就达到了Double Buffering的目的。
__shared__ float s_a[2][BK][BM];__shared__ float s_b[2][BK][BN];float r_load_a[4];float r_load_b[4];float r_comp_a[TM];float r_comp_b[TN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) > 5;int load_b_smem_n = (tid & 31) 性能如下所示,达到了理论峰值的 80.6%。
M N K =128128 1024, Time = 0.00024000 0.00024240 0.00025792 s, AVG Performance = 128.9191 GflopsM N K =192192 1024, Time = 0.00024000 0.00024048 0.00024125 s, AVG Performance = 292.3840 GflopsM N K =256256 1024, Time = 0.00024029 0.00024114 0.00024272 s, AVG Performance = 518.3728 GflopsM N K =384384 1024, Time = 0.00024070 0.00024145 0.00024198 s, AVG Performance =1164.8394 GflopsM N K =512512 1024, Time = 0.00024173 0.00024237 0.00024477 s, AVG Performance =2062.9786 GflopsM N K =768768 1024, Time = 0.00024291 0.00024540 0.00026010 s, AVG Performance =4584.3820 GflopsM N K = 1024 1024 1024, Time = 0.00024534 0.00024631 0.00024941 s, AVG Performance =8119.7302 GflopsM N K = 1536 1536 1024, Time = 0.00045712 0.00045780 0.00045872 s, AVG Performance =9829.5167 GflopsM N K = 2048 2048 1024, Time = 0.00089632 0.00089970 0.00090656 s, AVG Performance =8891.8924 GflopsM N K = 3072 3072 1024, Time = 0.00177891 0.00178289 0.00178592 s, AVG Performance = 10095.9883 GflopsM N K = 4096 4096 1024, Time = 0.00309763 0.00310057 0.00310451 s, AVG Performance = 10320.6843 GflopsM N K = 6144 6144 1024, Time = 0.00604826 0.00619887 0.00663078 s, AVG Performance = 11615.0253 GflopsM N K = 8192 8192 1024, Time = 0.01031738 0.01045051 0.01048861 s, AVG Performance = 12248.2036 GflopsM N K =1228812288 1024, Time = 0.02283978 0.02285837 0.02298272 s, AVG Performance = 12599.3212 GflopsM N K =1638416384 1024, Time = 0.04043287 0.04044823 0.04046151 s, AVG Performance = 12658.1556 Gflops
从 profiling 可以看到双倍的 Shared Memory 的占用

三、cuBLAS 实现方式探究
本节我们将认识CUDA的标准库——cuBLAS, 即NVIDIA版本的基本线性代数子程序 (Basic Linear Algebra Subprograms, BLAS) 规范实现代码。它支持 Level 1 (向量与向量运算) ,Level 2 (向量与矩阵运算) ,Level 3 (矩阵与矩阵运算) 级别的标准矩阵运算。
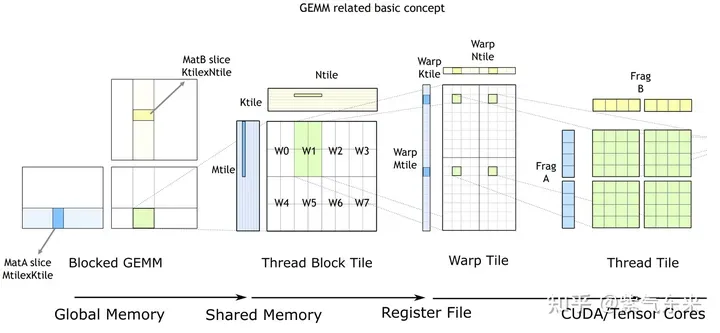
cuBLAS/CUTLASS GEMM的基本过程
如上图所示,计算过程分解成线程块片(thread block tile)、线程束片(warp tile)和线程片(thread tile)的层次结构并将AMP的策略应用于此层次结构来高效率的完成基于GPU的拆分成tile的GEMM。这个层次结构紧密地反映了NVIDIA CUDA编程模型。可以看到从global memory到shared memory的数据移动(矩阵到thread block tile);从shared memory到寄存器的数据移动(thread block tile到warp tile);从寄存器到CUDA core的计算(warp tile到thread tile)。
cuBLAS 实现了单精度矩阵乘的函数cublasSgemm,其主要参数如下:
cublasStatus_t cublasSgemm( cublasHandle_t handle, // 调用 cuBLAS 库时的句柄 cublasOperation_t transa, // A 矩阵是否需要转置 cublasOperation_t transb, // B 矩阵是否需要转置 int m, // A 的行数 int n, // B 的列数 int k, // A 的列数 const float *alpha, // 系数 α, host or device pointer const float *A, // 矩阵 A 的指针,device pointer int lda, // 矩阵 A 的主维,if A 转置, lda = max(1, k), else max(1, m) const float *B, // 矩阵 B 的指针, device pointer int ldb, // 矩阵 B 的主维,if B 转置, ldb = max(1, n), else max(1, k) const float *beta, // 系数 β, host or device pointer float *C, // 矩阵 C 的指针,device pointer int ldc // 矩阵 C 的主维,ldc >= max(1, m) );
调用方式如下:
cublasHandle_t cublas_handle;cublasCreate(&cublas_handle);float cublas_alpha = 1.0;float cublas_beta = 0;cublasSgemm(cublas_handle, CUBLAS_OP_N, CUBLAS_OP_N, N, M, K, &cublas_alpha, d_b, N, d_a, K, &cublas_beta, d_c, N);
性能如下所示,达到了理论峰值的 82.4%。
M N K =128128 1024, Time = 0.00002704 0.00003634 0.00010822 s, AVG Performance = 860.0286 GflopsM N K =192192 1024, Time = 0.00003155 0.00003773 0.00007267 s, AVG Performance =1863.6689 GflopsM N K =256256 1024, Time = 0.00003917 0.00004524 0.00007747 s, AVG Performance =2762.9438 GflopsM N K =384384 1024, Time = 0.00005318 0.00005978 0.00009120 s, AVG Performance =4705.0655 GflopsM N K =512512 1024, Time = 0.00008326 0.00010280 0.00013840 s, AVG Performance =4863.9646 GflopsM N K =768768 1024, Time = 0.00014278 0.00014867 0.00018816 s, AVG Performance =7567.1560 GflopsM N K = 1024 1024 1024, Time = 0.00023485 0.00024460 0.00028150 s, AVG Performance =8176.5614 GflopsM N K = 1536 1536 1024, Time = 0.00046474 0.00047607 0.00051181 s, AVG Performance =9452.3201 GflopsM N K = 2048 2048 1024, Time = 0.00077930 0.00087862 0.00092307 s, AVG Performance =9105.2126 GflopsM N K = 3072 3072 1024, Time = 0.00167904 0.00168434 0.00171114 s, AVG Performance = 10686.6837 GflopsM N K = 4096 4096 1024, Time = 0.00289619 0.00291068 0.00295904 s, AVG Performance = 10994.0128 GflopsM N K = 6144 6144 1024, Time = 0.00591766 0.00594586 0.00596915 s, AVG Performance = 12109.2611 GflopsM N K = 8192 8192 1024, Time = 0.01002384 0.01017465 0.01028435 s, AVG Performance = 12580.2896 GflopsM N K =1228812288 1024, Time = 0.02231159 0.02233805 0.02245619 s, AVG Performance = 12892.7969 GflopsM N K =1638416384 1024, Time = 0.03954650 0.03959291 0.03967242 s, AVG Performance = 12931.6086 Gflops
由此可以对比以上各种方法的性能情况,可见手动实现的性能已接近于官方的性能,如下:
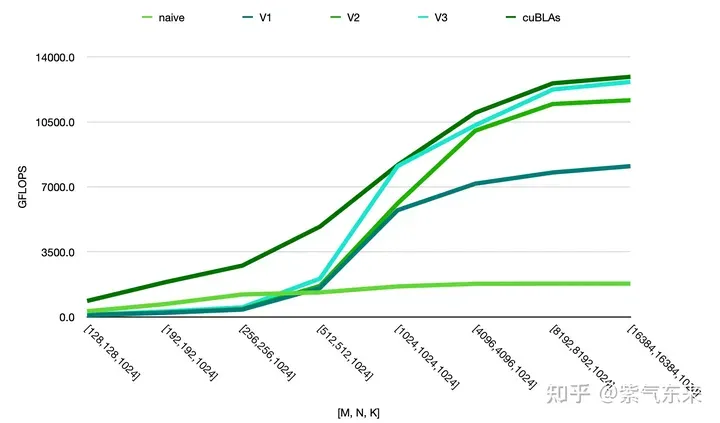
Das obige ist der detaillierte Inhalt vonCUDAs universelle Matrixmultiplikation: vom Einstieg bis zur Kompetenz!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Der jüngste Preis für Bitcoin in den Jahren 2018-2024 USD
Feb 15, 2025 pm 07:12 PM
Der jüngste Preis für Bitcoin in den Jahren 2018-2024 USD
Feb 15, 2025 pm 07:12 PM
Echtzeit-Bitcoin-USD-Preis Faktoren, die den Bitcoin -Preis beeinflussen Indikatoren für die Vorhersage zukünftiger Bitcoin -Preise Hier finden Sie einige wichtige Informationen zum Preis von Bitcoin in den Jahren 2018-2024:
 Welche Bibliotheken in GO werden von großen Unternehmen entwickelt oder von bekannten Open-Source-Projekten bereitgestellt?
Apr 02, 2025 pm 04:12 PM
Welche Bibliotheken in GO werden von großen Unternehmen entwickelt oder von bekannten Open-Source-Projekten bereitgestellt?
Apr 02, 2025 pm 04:12 PM
Welche Bibliotheken in GO werden von großen Unternehmen oder bekannten Open-Source-Projekten entwickelt? Bei der Programmierung in Go begegnen Entwickler häufig auf einige häufige Bedürfnisse, ...
 Vier Möglichkeiten zur Implementierung von Multithreading in C -Sprache
Apr 03, 2025 pm 03:00 PM
Vier Möglichkeiten zur Implementierung von Multithreading in C -Sprache
Apr 03, 2025 pm 03:00 PM
Multithreading in der Sprache kann die Programmeffizienz erheblich verbessern. Es gibt vier Hauptmethoden, um Multithreading in C -Sprache zu implementieren: Erstellen Sie unabhängige Prozesse: Erstellen Sie mehrere unabhängig laufende Prozesse. Jeder Prozess hat seinen eigenen Speicherplatz. Pseudo-MultitHhreading: Erstellen Sie mehrere Ausführungsströme in einem Prozess, der denselben Speicherplatz freigibt und abwechselnd ausführt. Multi-Thread-Bibliothek: Verwenden Sie Multi-Thread-Bibliotheken wie PThreads, um Threads zu erstellen und zu verwalten, wodurch reichhaltige Funktionen der Thread-Betriebsfunktionen bereitgestellt werden. Coroutine: Eine leichte Multi-Thread-Implementierung, die Aufgaben in kleine Unteraufgaben unterteilt und sie wiederum ausführt.
 Was wird in der C -Sprache allgemein verwendet?
Apr 03, 2025 pm 02:39 PM
Was wird in der C -Sprache allgemein verwendet?
Apr 03, 2025 pm 02:39 PM
Es gibt keine Funktion mit dem Namen "Sum" in der C -Sprachstandard -Bibliothek. "Summe" wird normalerweise von Programmierern definiert oder in bestimmten Bibliotheken bereitgestellt, und seine Funktionalität hängt von der spezifischen Implementierung ab. Gemeinsame Szenarien sind für Arrays summiert und können auch in anderen Datenstrukturen verwendet werden, z. B. in verknüpften Listen. Zusätzlich wird "Summe" auch in Bereichen wie Bildverarbeitung und statistischer Analyse verwendet. Eine ausgezeichnete "Summe" -Funktion sollte eine gute Lesbarkeit, Robustheit und Effizienz haben.
 Wie kann man das Größensymbol durch CSS anpassen und es mit der Hintergrundfarbe einheitlich machen?
Apr 05, 2025 pm 02:30 PM
Wie kann man das Größensymbol durch CSS anpassen und es mit der Hintergrundfarbe einheitlich machen?
Apr 05, 2025 pm 02:30 PM
Die Methode zur Anpassung der Größe der Größe der Größe der Größe in CSS ist mit Hintergrundfarben einheitlich. In der täglichen Entwicklung begegnen wir häufig Situationen, in denen wir die Details der Benutzeroberfläche wie Anpassung anpassen müssen ...
 Wie verwendet ich das Clip-Pfad-Attribut von CSS, um den 45-Grad-Kurveneffekt des Segmenters zu erreichen?
Apr 04, 2025 pm 11:45 PM
Wie verwendet ich das Clip-Pfad-Attribut von CSS, um den 45-Grad-Kurveneffekt des Segmenters zu erreichen?
Apr 04, 2025 pm 11:45 PM
Wie kann man den 45-Grad-Kurveneffekt des Segmenters erreichen? Bei der Implementierung des Segmenters verwandeln Sie den rechten Rand in eine 45-Grad-Kurve, wenn Sie auf die linke Schaltfläche klicken, und der Punkt ...
 Ist die H5-Seitenproduktion eine Front-End-Entwicklung?
Apr 05, 2025 pm 11:42 PM
Ist die H5-Seitenproduktion eine Front-End-Entwicklung?
Apr 05, 2025 pm 11:42 PM
Ja, die H5-Seitenproduktion ist eine wichtige Implementierungsmethode für die Front-End-Entwicklung, die Kerntechnologien wie HTML, CSS und JavaScript umfasst. Entwickler bauen dynamische und leistungsstarke H5 -Seiten auf, indem sie diese Technologien geschickt kombinieren, z. B. die Verwendung der & lt; canvas & gt; Tag, um Grafiken zu zeichnen oder JavaScript zu verwenden, um das Interaktionsverhalten zu steuern.
 Wie kann die technische Fragen und Antworten in der Chatgpt -Ära auf Herausforderungen reagieren?
Apr 01, 2025 pm 11:51 PM
Wie kann die technische Fragen und Antworten in der Chatgpt -Ära auf Herausforderungen reagieren?
Apr 01, 2025 pm 11:51 PM
Die technische Q & A -Community in der Chatgpt -Ära: SegmentFaults Antwortstrategie Stackoverflow ...



