Kann KI Fermats letzten Satz überwinden? Der Mathematiker gab fünf Jahre seiner Karriere auf, um 100 Beweisseiten in Code umzuwandeln

Der letzte Satz von Fermat steht kurz davor, von der KI erobert zu werden?

Und das Bedeutsamste an der ganzen Sache ist, dass der letzte Satz von Fermat, den die KI nun lösen wird, genau darin besteht, zu beweisen, dass KI nutzlos ist.

Einst gehörte die Mathematik zum Bereich der reinen menschlichen Intelligenz, heute wird dieses Gebiet von fortschrittlichen Algorithmen entschlüsselt und mit Füßen getreten.

Bilder

Der letzte Satz von Fermat ist ein „berüchtigtes“ Rätsel, das Mathematiker seit Jahrhunderten vor Rätsel stellt.

Es wurde 1993 bewiesen, und jetzt haben Mathematiker einen großen Plan: den Beweisprozess mithilfe von Computern zu reproduzieren.

Sie hoffen, dass in dieser Version des Beweises etwaige logische Fehler von einem Computer überprüft werden können.

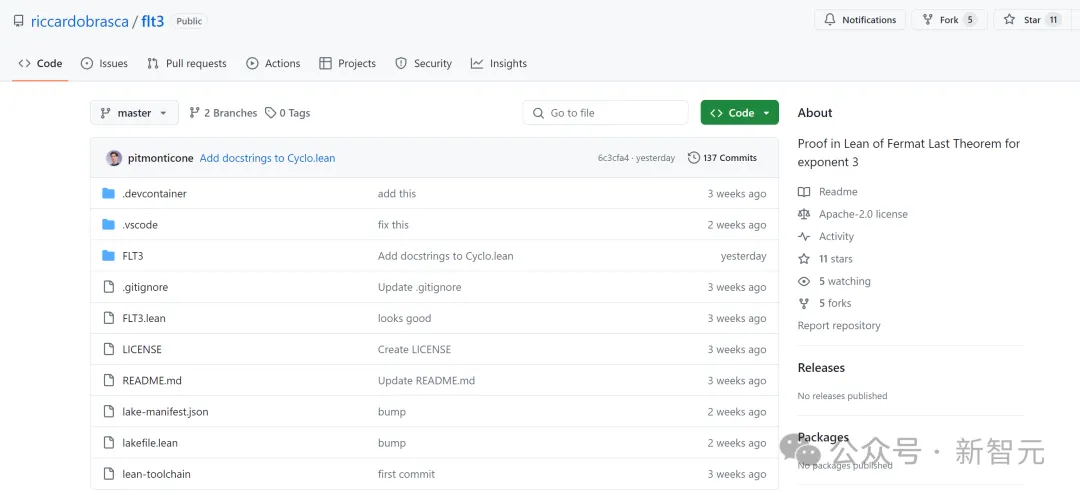
Projektadresse: https://github.com/riccardobrasca/flt3

Ende März sagte der Mathematiker Pietro Monticone aufgeregt, dass er und seine Kollegen Fermat mit Exponent 3 in der LeanProver-Formalisierung fast abgeschlossen hätten des letzten Satzes.

Sie werden den formalen Prozess so schnell wie möglich nach Mathlib portieren, um ihn im FLT-Projekt zu verwenden.

Bilder

Der Beweisprozess folgt in etwa dem Beweis von Wiles, jedoch mit geringfügigen Änderungen.

Verwenden Sie Lean, um Fermats letzten Satz in Code umzuwandeln

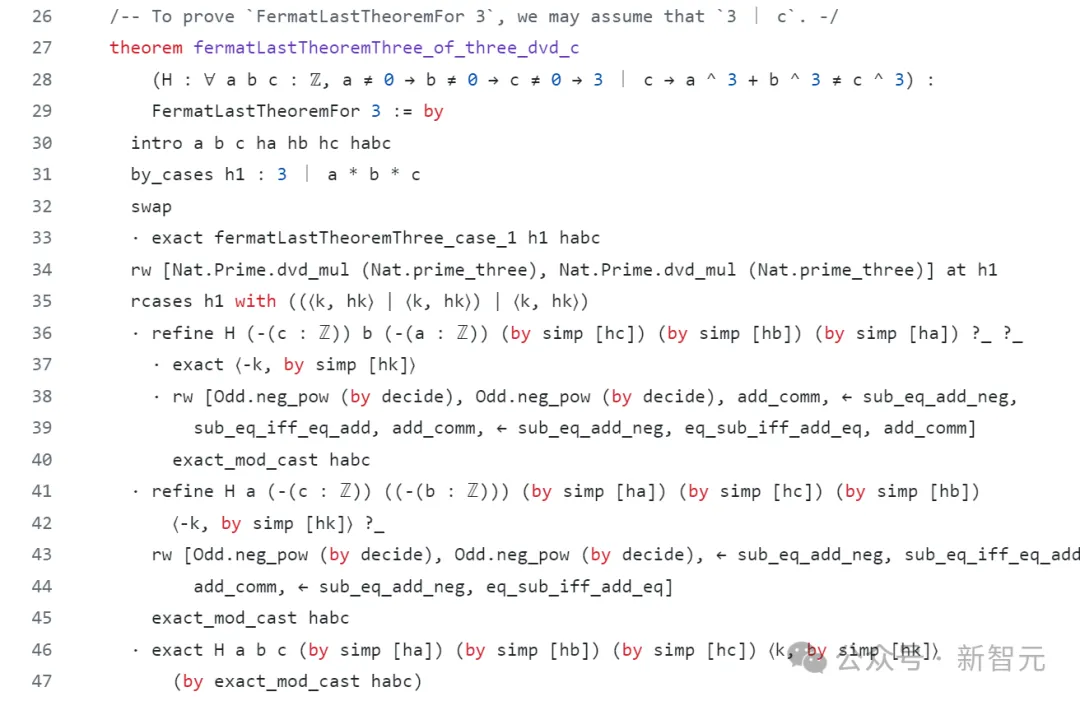
Im April wird der Mathematiker und Programmierer Kevin Buzzard diesen Plan veröffentlichen: den Beweis von Fermats letzten Satz durch Computercode zu vervollständigen.

Nachdem das Projekt im April online geht, wird der öffentliche Entwurf online erscheinen. Zu diesem Zeitpunkt kann jeder in der Lean-Community seinen eigenen Beitrag zum formellen Nachweis leisten.

Bilder

Einen bahnbrechenden 100-seitigen mathematischen Beweis in Computercode umwandeln. Ist dieser Prozess einfach zu implementieren?

Das ist natürlich dem Proof-Tool Lean zu verdanken, das von Terence Tao hoch gelobt und gerne verwendet wird und es Benutzern ermöglicht, Beweise im Prosastil zum Testen in Regeln und Logik umzuwandeln.

Bilder

Dieses Projekt ist jedoch nicht einfach und wird voraussichtlich viele Jahre dauern, und Kevin Buzzard Page erhielt finanzielle Unterstützung für das Projekt.

Bilder

Jeder versteht, dass es sich bei diesem Projekt wahrscheinlich um eine der bislang komplexesten computergestützten Demonstrationen handelt.

Bilder

Der letzte Satz von Fermat

Der letzte Satz von Fermat ist das aufregendste mathematische Rätsel der Geschichte.

Der Prozess des Beweises von Fermats letztem Satz ist direkt eine Geschichte der Mathematik.

Bilder

Der bekannte letzte Satz von Fermat wurde im 17. Jahrhundert vom französischen Mathematiker Pierre de Fermat vorgeschlagen. Leider konnte er zu Lebzeiten keine Beweise dafür finden.

Dieses Problem, das vor mehr als 300 Jahren entstand, hat die Menschheit drei Jahrhunderte lang direkt herausgefordert, die Welt viele Male schockiert, die Energie vieler der herausragendsten Gehirne der Menschheit erschöpft und Tausende von Amateuren fasziniert.

Bild

Dieser Satz besagt, dass es keine drei positiven ganzen Zahlen a, b, c gibt, die die Gleichung (a^n + b^n = c^n) erfüllen, wobei n eine beliebige ganze Zahl größer als ist 2 .

Die Schwierigkeit dieses Beweises besteht darin, dass es für Mathematiker schwierig ist, einen negativen Fall zu finden: Wie können wir garantieren, dass es keine solche unendliche ganze Zahl n gibt, die diese Gleichung erfüllen kann?

Bilder

Glücklicherweise ist es für heutige Mathematiker nichts Neues, das Konzept der Unendlichkeit in Logik umzuwandeln.

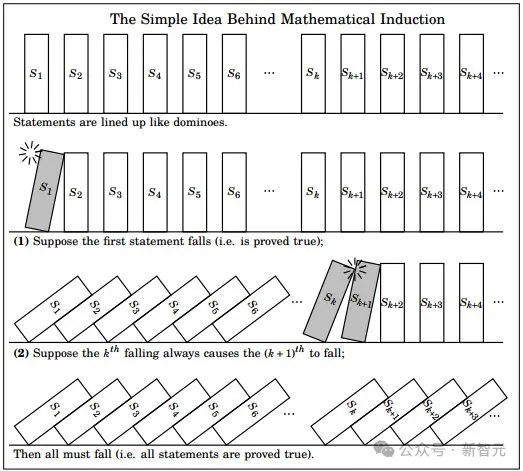
Im einfacheren Beweis können wir uns auf Induktion verlassen –

Sobald eine bestimmte Logik für eine bestimmte Zahl (z. B. 8) wahr ist, gilt sie auch für jede nachfolgende Zahl (z. B. 9, 10). , 11 usw.) gelten bis ins Unendliche gleichermaßen.

Bilder

Allerdings war Fermats letzter Satz seit Hunderten von Jahren ein Stolperstein in der mathematischen Welt.

Erst 1993 löste der britische Mathematiker Andrew Wiles dieses Rätsel mit einem 100-seitigen schriftlichen Beweis.

Bilder

Warum können Computer Fermats letzten Satz nicht beweisen?

Die Industrie ist der Ansicht, dass es drei Gründe gibt:

1 erscheinen flüchtige Fehler

Zum Glück gibt es einen Lean-Hilfsbeweis

Ein 100-seitiger mathematischer Beweis ist nicht so einfach zu kontrollieren, egal ob für normale Mathematikstudenten oder Mathematiker.

Glücklicherweise können wir uns nicht mehr auf traditionelle Beweismethoden verlassen und können auf Tools wie Lean zurückgreifen.

Es handelt sich um ein auf C++ basierendes Programmiertool, das speziell zum Schreiben und Überprüfen von Induktionsbeweisen entwickelt wurde.

Viele der sogenannten „künstlichen Intelligenz“ von heute sind nichts anderes als geschickt arrangierte Wörter, die die menschliche Sprache imitieren. Aber computergestützte Beweise wie Lean integrieren menschliches Denken und computergestützte erweiterte Fähigkeiten stärker.

Bilder

Lean-Programmiertools halten Einzug in die Grundschulklassen

Kevin Buzzard, der Mathematik am Imperial College London unterrichtet, hat mehrere Jahre damit verbracht, mit dem Lean-Tool Unterstützung für den gesamten Mathematik-Grundkurs des Colleges zu entwickeln.

Mithilfe dieser Tools können Schüler im Unterricht besprochene Inhalte in Schritte logischer und mathematischer Operationen aufteilen.

Das ist wie der Rosetta-Stein der mathematischen Beweise.

Clarissa Littler, die auch Mathematiklehrerin ist, stimmt Kevin Buzzards Philosophie voll und ganz zu.

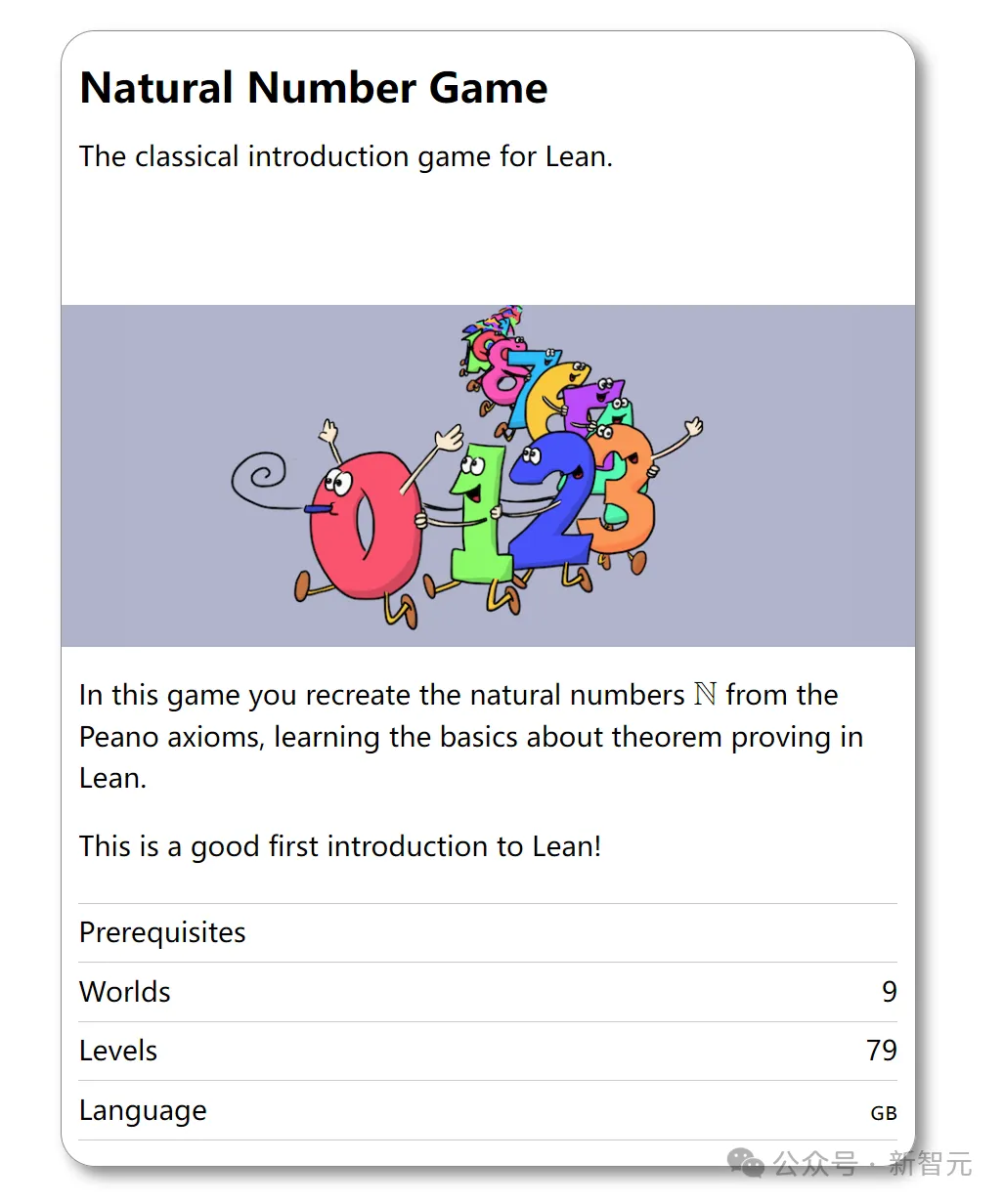
Sie unterrichtet diskrete Mathematik am Portland Community College. In den vergangenen zwei Semestern nutzte sie in ihrem diskreten Mathematikunterricht das von Kevin Buzzard entwickelte „Lean Classic Introductory Game“.

Bilder

Adresse: https://adam.math.hhu.de/

Sie wird das „Spiel mit natürlichen Zahlen“ verwenden, um Schülern dabei zu helfen, sich mit der Idee der mathematischen Induktion vertraut zu machen, und durch das „Spiel zur Mengenlehre“ wird sie sie an das Denken über Mengen gewöhnen.

Bilder

In diesem Prozess wird die Verständnislücke der Schüler zwischen „strikter Befolgung logischer Regeln beim Schreiben von Beweisen“ und „Verwendung populärer Sprache zur Erklärung der Wahrheit der Dinge“ schrittweise geschlossen.

Littler betonte, dass ein Hauptaugenmerk des Kurses darin liegt, Studierenden mit schwachen mathematischen Grundlagen zu ermöglichen, freier im Sinne von Mathematikern zu denken und gleichzeitig Beweise, Beweise und Methoden zur Wahrheitsdarstellung besser zu verstehen.

Dieser Übergang von der formalen Logik zu Regellisten und zum Ausdruck in Prosa ist der Schlüssel zur Aufteilung von Projekten in kooperierende Codeteile.

Bilder

Und das ist besonders wichtig an der Schnittstelle von Programmierung und reiner Mathematik, und hier können Tools wie Lean glänzen.

Buzzard sagte, er hoffe, die komplexen mathematischen Ideen, die durch Fermats letzten Satz ausgelöst werden, in eine programmierbare Form umzuwandeln.

Im Laufe der Jahrhunderte wurden viele wertvolle neue Zweige der Mathematik geschaffen, um diesen Satz zu beweisen, der nach Buzzards Meinung „ohne praktische Bedeutung“ ist.

Ja, nach Buzzards Ansicht ist Fermats letzter Satz bedeutungslos und hat in der realen Welt keine Anwendung. Aufgrund dieses „berüchtigten“ Problems sind jedoch in den letzten Jahren viele brillante neue Ideen entstanden.

Die Umwandlung von Wiles' 100-seitigem Beweis in eine formale Sprache und Regeln, die Computer verstehen können, dürfte einer neuen Generation von Mathematikern die Tür zu computergestützten Beweisen öffnen.

Bilder

Und dieses Konvertierungstool kann auch Programmierern helfen.

Littler sagte, dass ehrgeizige Projekte in diesem Bereich immer einen Versuch wert seien, weil wir alle von den gewonnenen Erkenntnissen und den geschriebenen Bibliotheken profitieren können.

Obwohl die interaktive Beweisführung von Theoremen noch ein relativ neues Feld ist, hat die Lean-Community viel hervorragende Arbeit geleistet.

Kevin Buzzard: Evangelist von Lean

Kevin Mark Buzzard, geboren 1968, verfügt über fundierte berufliche Kenntnisse in arithmetischer Geometrie und Langlands-Programmen.

Er ist derzeit Professor für reine Mathematik am Imperial College London und der „Evangelist“ des KI-Tools Lean.

Während seines Studiums an der Royal Grammar School nahm Kevin Buzzard an der Internationalen Mathematikolympiade teil und gewann 1986 die Bronzemedaille und 1987 mit perfekten Ergebnissen die Goldmedaille.

Bilder

Anschließend schloss er sein Grundstudium der Mathematik am Trinity College der Universität Cambridge ab und erhielt 1990 den Titel „Senior Wrangler“ und 1991 den C.A.S.M.-Abschluss.

Unter der Leitung von Richard Taylor wurde 1995 seine Doktorarbeit „Die Ebenen modularer Darstellungen“ fertiggestellt, in der er ein komplexes Gebiet der Mathematik erforschte.

Bilder

1998 begann er als Dozent am Imperial College London zu arbeiten, wurde 2002 zum Senior Lecturer befördert und 2004 zum Professor ernannt.

Er führte außerdem Gastforschungen an der Harvard University (Oktober bis Dezember 2002) und mehreren anderen berühmten Institutionen durch.

Für seine herausragenden Beiträge auf dem Gebiet der Zahlentheorie gewann er 2002 den Whitehead Award und 2008 den Senior Berwick Award.

Im Jahr 2017 startete Buzzard ein Projekt und einen Blog über Lean Theorem Prover, der sich der Förderung des Einsatzes computergestützter Beweiswerkzeuge in der mathematischen Forschung widmet.

Er begleitete auch den Musiker Dan Snaith (Künstlername Caribou) bei der Fertigstellung seiner mathematischen Doktorarbeit über das Studium superkonvergenter Siegel-Modulsymbole, für die Snaith am Imperial College London promovierte.

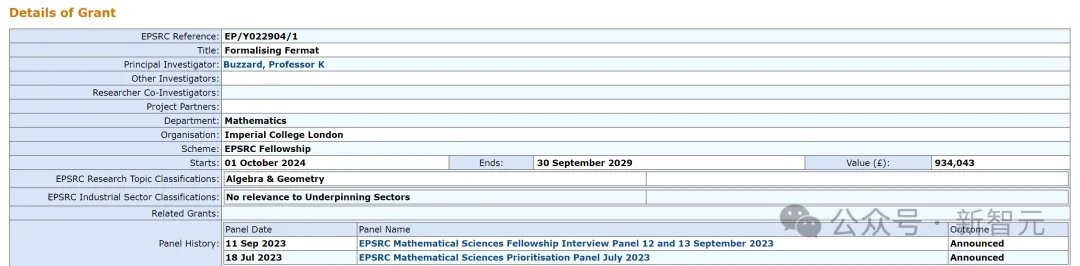
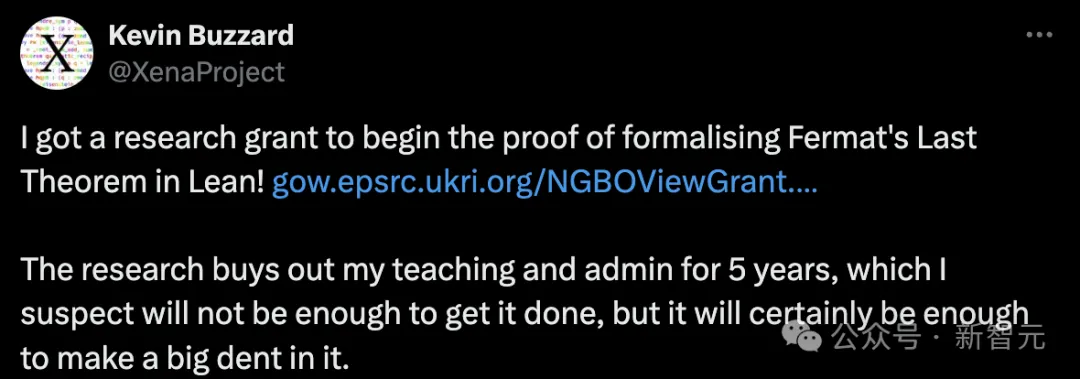
Im Oktober 2023 erklärte Kevin Buzzard in den sozialen Medien, dass er Forschungsgelder erhalten habe und begonnen habe, Lean zu nutzen, um Fermats letzten Satz zu beweisen.

Bilder

Buzzard sagte: „Vor zehn Jahren hätte das unendlich viel Zeit gekostet.“ Um das Projekt abzuschließen, wird er seine Lehrtätigkeit für fünf Jahre ruhen lassen.

Lohnt es sich, die eigenen Aufgaben auf Eis zu legen?

Nach Meinung seines Kollegen Chris Williams von der University of Nottingham im Vereinigten Königreich könnte ein solches Projekt unerwartete Vorteile und weitreichende Auswirkungen haben.

„Ich halte es für unwahrscheinlich, dass er den gesamten Beweis in den nächsten fünf Jahren offiziell formalisieren wird, sonst wäre es erstaunlich. Allerdings sind viele Werkzeuge mittlerweile in der Zahlentheorie und der arithmetischen Geometrie allgegenwärtig, daher prognostiziere ich, dass dies in Zukunft der Fall sein wird Erhebliche Fortschritte werden sehr nützlich sein.

Mit der kontinuierlichen Weiterentwicklung der Computerwerkzeuge verschwimmen die Grenzen zwischen verschiedenen Zweigen der Mathematik und sogar zwischen verschiedenen Disziplinen immer mehr, was zur Entstehung einiger Beweise geführt hat, die fast unmöglich zu überprüfen sind.

Zum Beispiel schrieb der japanische Mathematiker Mochizuki Shinichi von der Universität Kyoto einen 500-seitigen Beweis, dessen Veröffentlichung mehrere Jahre dauerte, weil er so kompliziert war, auch weil die Leute nicht wussten, was sie damit anfangen sollten.

Von nun an werden wir möglicherweise feststellen, dass die Grenzen der Mathematik immer mehr verschwimmen.

Dabei geht es nicht um Wahrhaftigkeit oder logische Mehrdeutigkeit, sondern um die Bandbreite unterschiedlicher Ideen, die in einen Beweis einfließen können.

Lean ermöglicht es Mathematikern, ihre Ideen in Code umzuwandeln, was es für Kollegen einfacher macht, sie zu verstehen. Anhand der von Vorgängern aufgezeichneten Präzedenzfälle können künftige Mathematiker auf dieser Grundlage ihre eigene Forschung weiter vorantreiben.

Buzzard sagte, dass das Merkmal des mathematischen Schreibens in Lean darin besteht, dass man präzise angegebene, aber unbewiesene Ergebnisse hinterlassen kann und andere sie später lösen können.

Lean selbst erleichtert einen solchen Arbeitsablauf.

Bilder

Mit anderen Worten: Fermats letzter Satz bereitet sich darauf vor, durch „Crowdsourcing“ gelöst zu werden – insbesondere wenn die Codierungsarbeit Buzzards verbleibende Arbeitsjahre übersteigt.

Das Vervollständigen eines mathematischen Beweises erfordert die Anstrengungen der gesamten Community.

Vielleicht können wir in Zukunft eine ähnliche Plattform wie Genius.com für den Austausch und die Interpretation mathematischer Beweise haben.

Referenzen:

https://www.php.cn/link/845375903f6dbadda379558e905089f2

https://www.php.cn/link/08b136 650 4a4a5a1e679e2eaad38b595

Das obige ist der detaillierte Inhalt vonKann KI Fermats letzten Satz überwinden? Der Mathematiker gab fünf Jahre seiner Karriere auf, um 100 Beweisseiten in Code umzuwandeln. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!