Photoshop制作标准椭圆矩形的三种方法
今天小编教大家使用Photoshop制作椭圆矩形的三种方法,很适合初学者学习,感兴趣的朋友可以一起来学习
椭圆矩形介于圆和圆角矩形中间的形状,主题图标绘制最流行的形状之一;有一些新人和身边朋友问我怎么制作这形状,所以,分享一下我的绘制方法。
最终效果
准备工作:
打开Photoshop,新建600 * 600的画布,其它参数默认,点确定。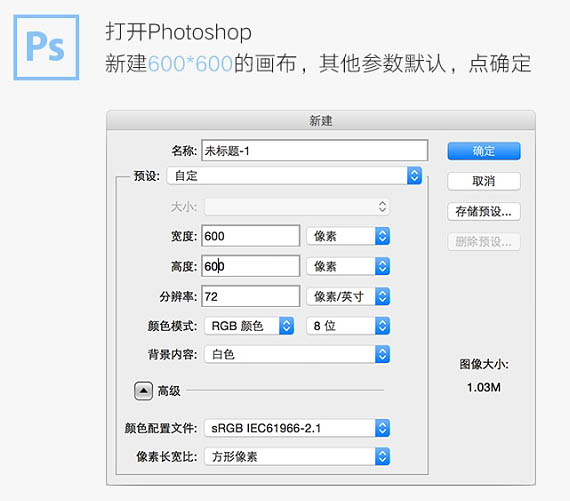
方法1:
鼠标移至左侧工具栏矩形工具上,点击三角箭头切换成多边形工具。鼠标移至选项栏设置边:4,点击设置图标(齿轮),按下展开,勾选平滑拐角。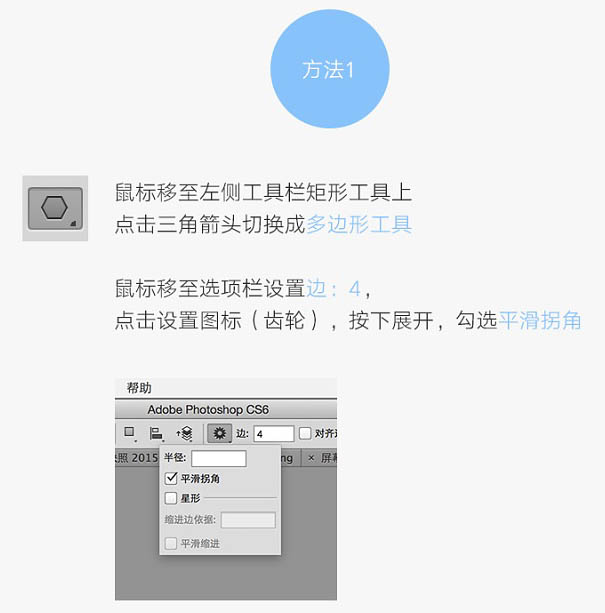
按住Shift,按住鼠标左键在画布中央绘制就可以了。
放大之后发现它的边缘是虚的像素,为了更加精确的显示,要让边缘对齐像素网格。
左击首选项 > 常规,勾选最后一条让矢量工具与变化的像素网格对齐。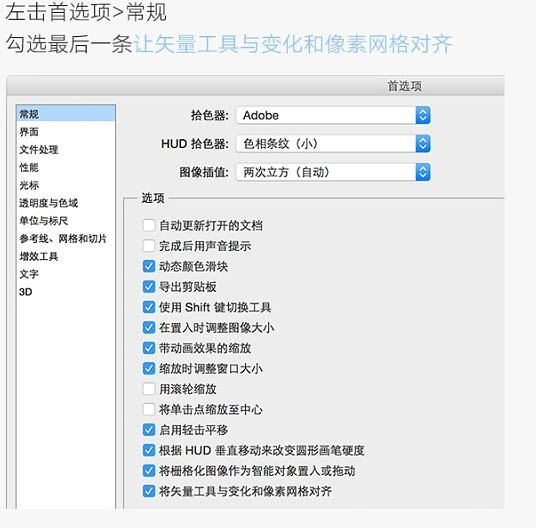
设置好后,回到画布Ctrl + T选中形状,按住左键轻轻移动鼠标形状图形就自动对齐像素网格。
这个是最快速简单的一种方法,如果需要调整角度大小,精确的做法是用直接选择工具依次对四条边的锚点向内或向外进行移动。
方法2:
选择圆角矩形工具,点击画布,设置弹窗的参数。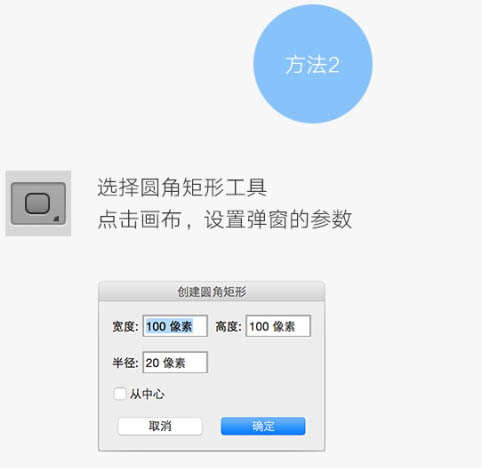
点确定,绘制出一个圆角矩形。
可以看出来圆角矩形与椭圆矩形的区别,就是在四条边向外微微弯曲,所以只要在圆角矩形基础上添加向外的弧形就可以。选择椭圆工具,选项栏选择合并形状。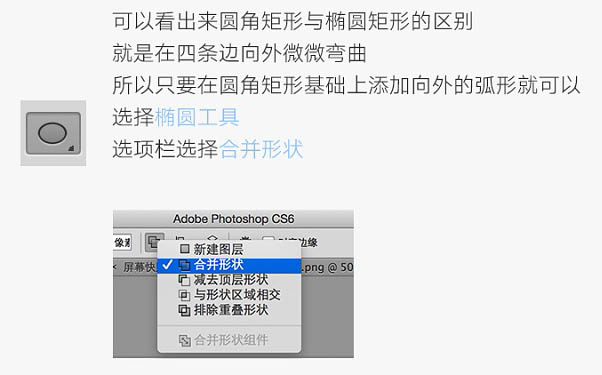
在圆角矩形上添加椭圆形状,椭圆两端的弧度要与圆角矩形两端的弧度重合,这样才平滑。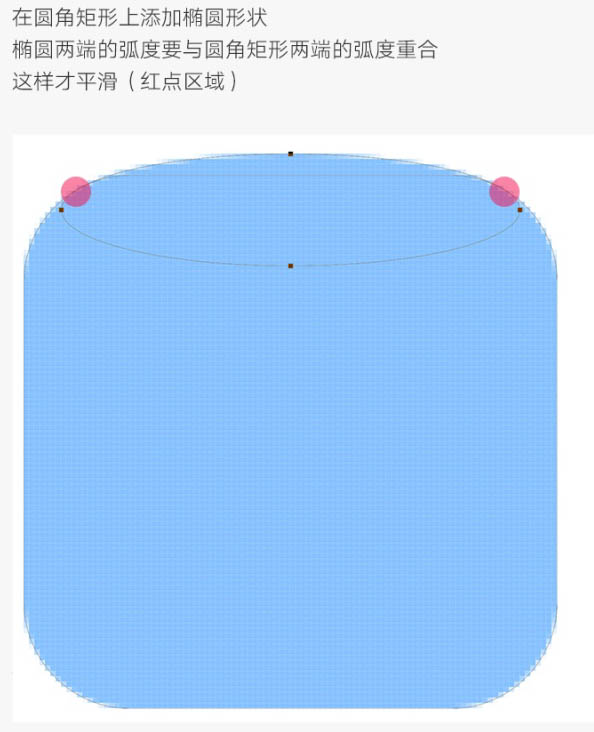
复制、粘贴椭圆,添加至其他三条边,完成。
方法3:
选择椭圆工具,点击画布,设置弹窗的参数。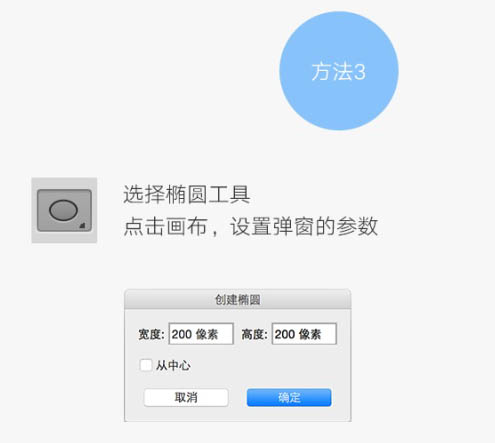
点确定,绘制一个圆形。
选中圆形,复制,粘贴,按住Shift和鼠标左键向上或下移动90px。
选项栏选择与形状区域相交。
选中两个圆,复制,粘贴。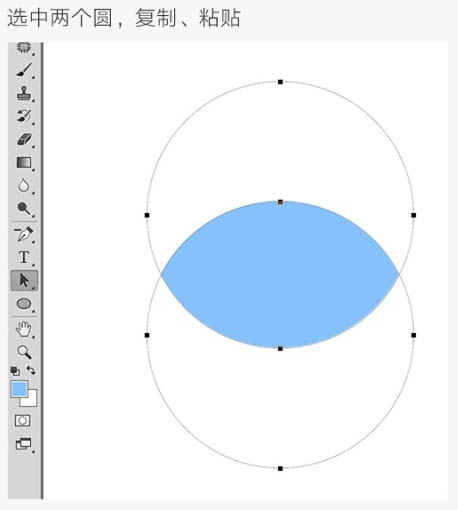
旋转90度。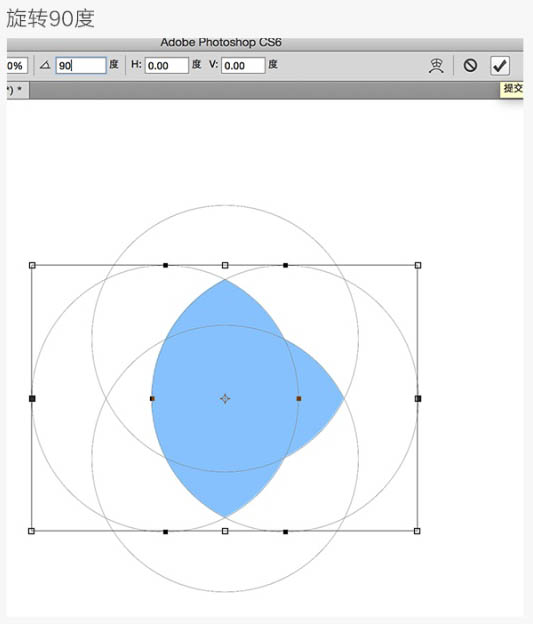
选中左边的圆,选项栏选择与形状区域相交。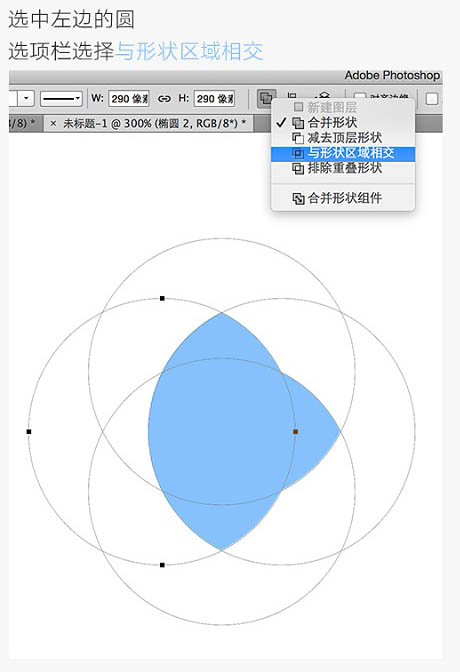
点击,形成下图的形状图形,已经像椭圆矩形了,只是四个角不是圆角。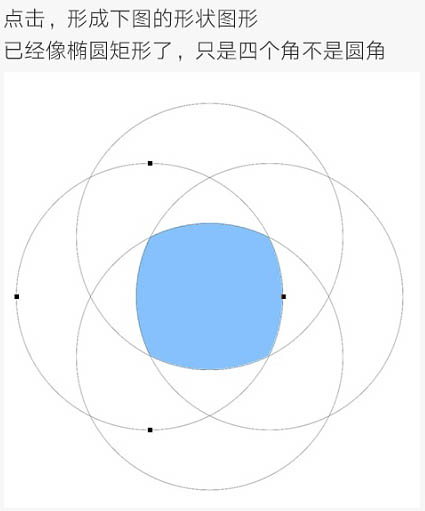
把尖角变成圆角,选择椭圆工具,选项栏选择合并形状,添加74px的圆形,注意两个图形要重合才能圆滑。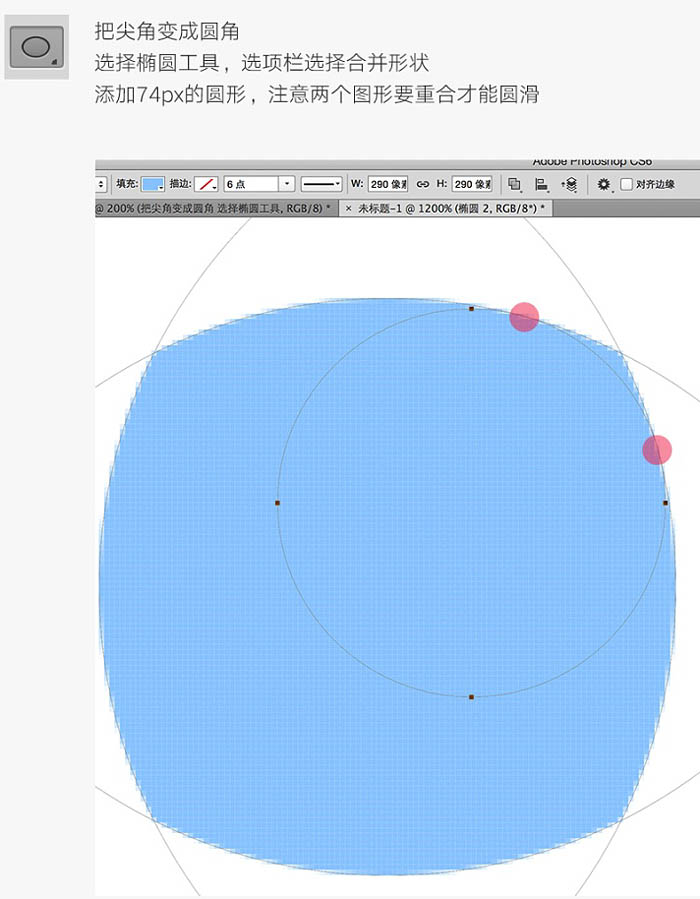
选择矩形工具,选项选择“减去顶层形状”,沿着重合点减去矩形。
选中圆形,复制,然后删除圆形,粘贴,尖角变成圆角。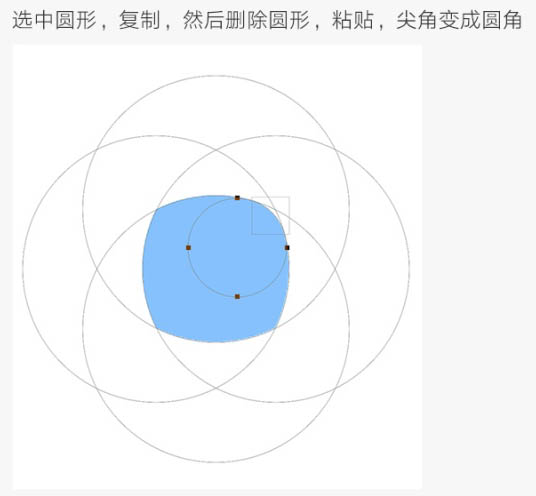
选中圆形和矩形,复制,粘贴,自由变换,垂直翻转。
移至右下角,边缘重合。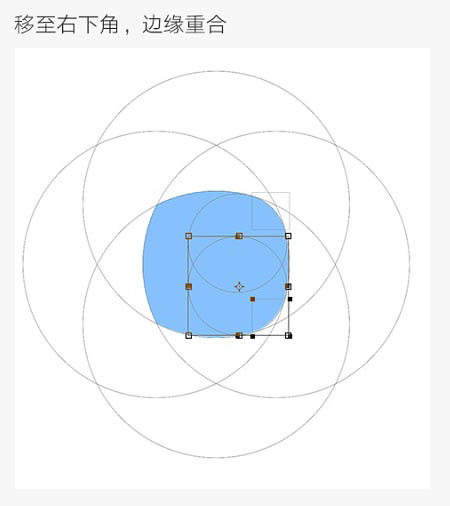
左边也使用同样的步骤。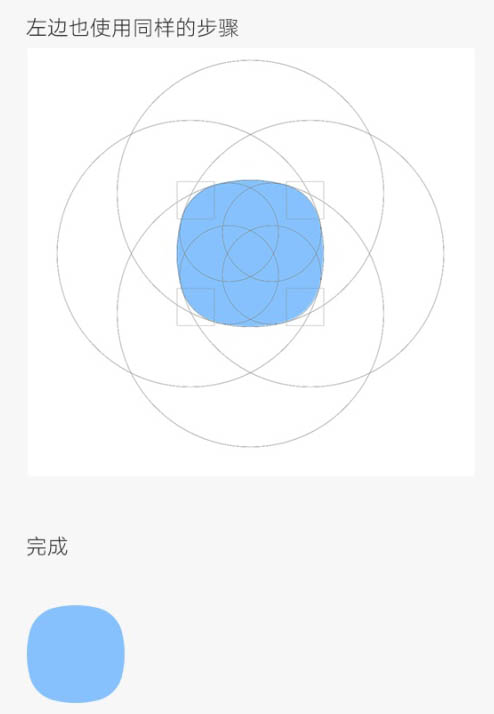
内圆调整圆角大小。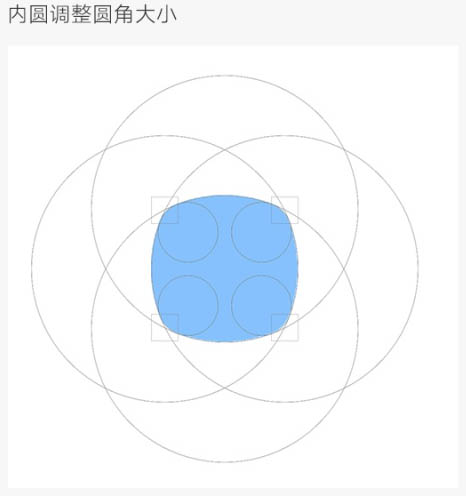
外圆调整弧度大小。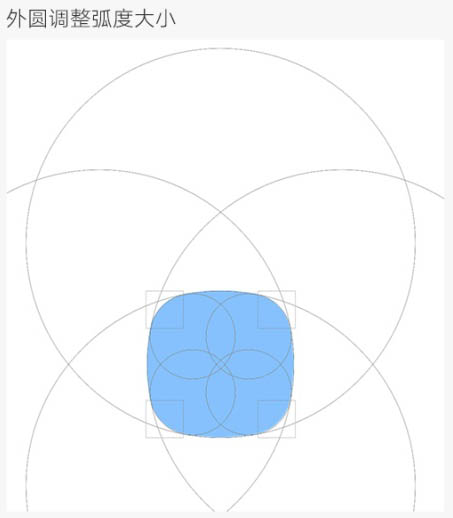
最终效果:

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
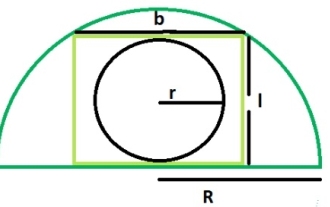 Wie groß ist die Fläche eines Kreises innerhalb eines Rechtecks, das in einen Halbkreis eingeschrieben ist?
Sep 13, 2023 am 08:45 AM
Wie groß ist die Fläche eines Kreises innerhalb eines Rechtecks, das in einen Halbkreis eingeschrieben ist?
Sep 13, 2023 am 08:45 AM
Ein in ein Rechteck eingeschriebener Kreis tangiert die längere Seite des Rechtecks, d. h. seine Länge tangiert den Kreis. Ein in einen Halbkreis eingeschriebenes Rechteck berührt zwei Punkte auf dem Bogen des Halbkreises. Die Breite des Rechtecks entspricht dem Durchmesser des Kreises. Wenn R der Radius des Halbkreises ist. Die Länge des Rechtecks = √2R/2 Die Breite des Rechtecks = R/√2 Der Radius des eingeschriebenen Kreises beträgt r = b/2 = R/2√2 Mit dieser Formel können wir das in den Halbkreis eingeschriebene Rechteck berechnen Die Fläche eines Kreises, Fläche = (π*r2)=π*R/8 Beispieldemonstration #include<stdio.h>intmain(){&
 So führen Sie eine Grafik zusammen, nachdem CAD-Rechtecke verstreut sind
Feb 28, 2024 pm 12:10 PM
So führen Sie eine Grafik zusammen, nachdem CAD-Rechtecke verstreut sind
Feb 28, 2024 pm 12:10 PM
Bei der Verwendung von CAD-Software kommt es häufig vor, dass wir „verstreute“ rechteckige Objekte wieder zu einer einzigen Grafik zusammenfügen müssen. Dieser Bedarf entsteht in vielen Bereichen, beispielsweise in der Raumplanung, im mechanischen Design und in Architekturzeichnungen. Um dieser Nachfrage gerecht zu werden, müssen wir einige Schlüsselfunktionen der CAD-Software verstehen und beherrschen. Als Nächstes stellt Ihnen der Herausgeber dieser Website ausführlich vor, wie Sie diese Aufgabe in der CAD-Umgebung ausführen. Benutzer, die Zweifel haben, können diesem Artikel folgen, um mehr zu erfahren. Methode zum Zusammenführen von CAD-Rechtecken zu einer Grafik nach dem Aufteilen: 1. Öffnen Sie die CAD2023-Software, erstellen Sie ein Rechteck und geben Sie dann den X-Befehl und ein Leerzeichen ein. Wie unten gezeigt: 2. Wählen Sie das rechteckige Objekt aus und platzieren Sie es. Sie können die Objekte aufteilen. 3. Wählen Sie alle offenen Leitungen aus
 Schreiben Sie ein Java-Programm, um die Fläche und den Umfang eines Rechtecks mithilfe des Klassenkonzepts zu berechnen
Sep 03, 2023 am 11:37 AM
Schreiben Sie ein Java-Programm, um die Fläche und den Umfang eines Rechtecks mithilfe des Klassenkonzepts zu berechnen
Sep 03, 2023 am 11:37 AM
Die Java-Sprache ist heute eine der am häufigsten verwendeten objektorientierten Programmiersprachen der Welt. Das Konzept der Klassen ist eines der wichtigsten Merkmale objektorientierter Sprachen. Eine Klasse ist wie eine Blaupause für ein Objekt. Wenn wir zum Beispiel ein Haus bauen wollen, erstellen wir zunächst einen Bauplan des Hauses, also einen Plan, der zeigt, wie wir das Haus bauen werden. Nach diesem Plan können wir viele Häuser bauen. Ebenso können wir mithilfe von Klassen viele Objekte erstellen. Klassen sind Blaupausen für die Erstellung vieler Objekte, wobei Objekte reale Einheiten wie Autos, Fahrräder, Stifte usw. sind. Eine Klasse hat die Eigenschaften aller Objekte und die Objekte haben die Werte dieser Eigenschaften. In diesem Artikel schreiben wir ein Java-Programm, um den Umfang und die Flächen eines Rechtecks mithilfe des Klassenkonzepts zu ermitteln
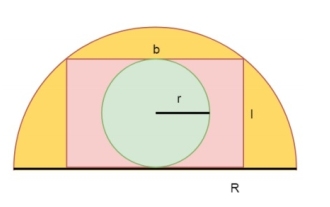 Wie groß ist die Fläche eines Kreises innerhalb eines Rechtecks, das in einen Halbkreis eingeschrieben ist?
Sep 04, 2023 pm 11:33 PM
Wie groß ist die Fläche eines Kreises innerhalb eines Rechtecks, das in einen Halbkreis eingeschrieben ist?
Sep 04, 2023 pm 11:33 PM
Betrachten wir einen gegebenen Halbkreis. Sein Radius ist R. In den Halbkreis ist ein Rechteck der Länge l und der Breite b eingeschrieben. In das Rechteck ist nun ein Kreis mit dem Radius r eingeschrieben. Wir müssen die Fläche des inneren Kreises finden. Wir wissen, dass die Länge des größten in einen Halbkreis eingeschriebenen Rechtecks l und die Breite b ist, dann lauten die Gleichungen von l und b wie folgt: Nun ist der Radius des größten Kreises, der in ein Rechteck eingeschrieben werden kann, r als folgt -
 So wählen Sie ein Rechteck in Word aus
Mar 16, 2023 am 11:29 AM
So wählen Sie ein Rechteck in Word aus
Mar 16, 2023 am 11:29 AM
So wählen Sie ein Rechteck in Word aus: 1. Öffnen Sie ein Word-Dokument und gehen Sie zur Startseite des Dokuments. 2. Geben Sie den erforderlichen Dateninhalt in das Dokument ein. 3. Suchen Sie die Alt-Taste auf der Tastatur und halten Sie sie gedrückt Wählen Sie gleichzeitig mit der Maus den Bereich aus, der ein Rechteck benötigt.
 C-Programm für Fläche und Umfang eines Rechtecks
Sep 20, 2023 am 10:41 AM
C-Programm für Fläche und Umfang eines Rechtecks
Sep 20, 2023 am 10:41 AM
Angesichts der Länge und Breite eines Rechtecks müssen wir seine Fläche und seinen Umfang ermitteln. Ein Rechteck ist eine zweidimensionale Form mit vier Seiten und vier Ecken, die jeweils einen Winkel von 90 Grad bilden. Nicht alle Seiten eines Rechtecks sind gleich, nur die gegenüberliegenden Seiten des Rechtecks sind gleich. Auch die Diagonalen eines Rechtecks sind gleich lang. Unten sehen Sie ein Diagramm eines Rechtecks. Dabei repräsentiert A die Breite des Rechtecks und B die Länge des Rechtecks. Um die Fläche eines Rechtecks zu ermitteln, lautet die Formel: Länge x Breite. Der Umfang eines Rechtecks beträgt 2x (Länge + Breite). BeispielEingabe: 2030Ausgabe: Fläche des Rechtecks ist: 600 Umfang des Rechtecks ist: 100Algorithmus START&a
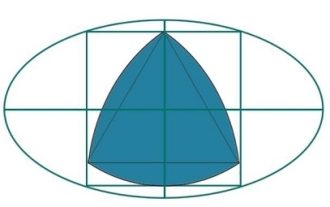 Was ist das größte Reuleaux-Dreieck innerhalb eines Quadrats, das in eine Ellipse eingeschrieben ist?
Aug 29, 2023 pm 08:49 PM
Was ist das größte Reuleaux-Dreieck innerhalb eines Quadrats, das in eine Ellipse eingeschrieben ist?
Aug 29, 2023 pm 08:49 PM
Hier sehen wir die Fläche des größten Ruhrdreiecks eingeschrieben in ein Quadrat, das wiederum in eine Ellipse eingeschrieben ist. Wir wissen, dass die Länge der Hauptachse der Ellipse 2a und die Länge der Nebenachse 2b beträgt. Die Seitenlänge des Quadrats beträgt „x“ und die Höhe des Luer-Dreiecks beträgt h. Wir wissen, dass ein in eine Ellipse mit der Hauptachse 2a und der Nebenachse 2b eingeschriebenes Quadrat die Seitenlänge − hat und die Höhe eines Ruhrdreiecks gleich a ist. Also h=x. Daher beträgt die Fläche des Ruhrdreiecks −. Beispiel#include<iostream>#include<cmath>usingnamespacestd;floata
 Wie groß ist die Fläche der größtmöglichen Raute, die in ein Rechteck eingeschrieben werden kann?
Sep 03, 2023 pm 08:01 PM
Wie groß ist die Fläche der größtmöglichen Raute, die in ein Rechteck eingeschrieben werden kann?
Sep 03, 2023 pm 08:01 PM
Eine in ein Rechteck eingeschriebene Raute verläuft tangential zu den Seiten des Rechtecks, sodass wir daraus schließen können, dass die Diagonalen der größten eingeschriebenen Raute gleich der Länge und Breite des Rechtecks sind. Wenn wir die Länge (l) und die Breite (b) des Rechtecks haben, sind die Diagonallängen der größten eingeschriebenen Raute d1=l und d2=b. Die Fläche einer Raute ergibt sich aus der Formel Fläche=(d1*d2)/2. Durch Ersetzen der Werte von d1 und d2 erhalten wir: Fläche=(l*b)/2 Mit dieser Formel können wir Erstellen Sie eine Berechnung, die innerhalb eines Programms durchgeführt werden kann, um die Fläche des größten aus einem Rechteck geschnittenen Rhombus zu berechnen, Beispiel Echtzeitdemonstration #include<stdio.h>intmain(){ float






