 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Transformer will Kansformer werden? Es hat Jahrzehnte gedauert, bis MLP den Herausforderer KAN an die Spitze brachte
Transformer will Kansformer werden? Es hat Jahrzehnte gedauert, bis MLP den Herausforderer KAN an die Spitze brachte
Transformer will Kansformer werden? Es hat Jahrzehnte gedauert, bis MLP den Herausforderer KAN an die Spitze brachte
MLP (Multilayer Perceptron) wird seit Jahrzehnten verwendet. Gibt es wirklich keine andere Wahl?
Multilayer Perceptron (MLP), auch bekannt als Fully Connected Feedforward Neuronales Netzwerk, ist der grundlegende Baustein der heutigen Deep-Learning-Modelle.
Die Bedeutung von MLPs kann nicht genug betont werden, da sie die Standardmethode zur Approximation nichtlinearer Funktionen beim maschinellen Lernen sind.
Ist MLP jedoch der beste nichtlineare Regressor, den wir erstellen können? Obwohl MLPs weit verbreitet sind, weisen sie erhebliche Nachteile auf. Beispielsweise verbrauchen MLPs in Transformer-Modellen fast alle nicht eingebetteten Parameter und sind im Vergleich zu Aufmerksamkeitsschichten ohne Nachbearbeitungsanalysetools im Allgemeinen weniger interpretierbar.
Gibt es also eine Alternative zu MLP?
Heute ist KAN erschienen.


Dies ist ein Netzwerk, das vom Kolmogorov-Arnold-Darstellungssatz inspiriert ist.
Link: https://arxiv.org/pdf/2404.19756
Github: https://github.com/KindXiaoming/pykan
Sobald die Studie veröffentlicht wurde, sorgte sie für Aufsehen auf ausländischen sozialen Plattformen große Aufmerksamkeit und Diskussion.
Einige Internetnutzer sagten, Kolmogorov habe das mehrschichtige neuronale Netzwerk bereits 1957 entdeckt, viel früher als Rumerhart, Hinton und Williams 1986er Artikel, aber er wurde vom Westen ignoriert.

Einige Internetnutzer sagten auch, dass die Veröffentlichung dieses Papiers bedeutet, dass der Todesstoß für tiefes Lernen geläutet wurde.

Einige Internetnutzer fragten sich, ob diese Forschung genauso störend sein würde wie das Transformer-Papier.

Aber einige Autoren sagten, dass sie 2018-19 das Gleiche auf der Grundlage der verbesserten Kolmogrov-Gabor-Technik getan hätten.
Als nächstes werfen wir einen Blick darauf, worum es in diesem Papier geht.
Papierübersicht
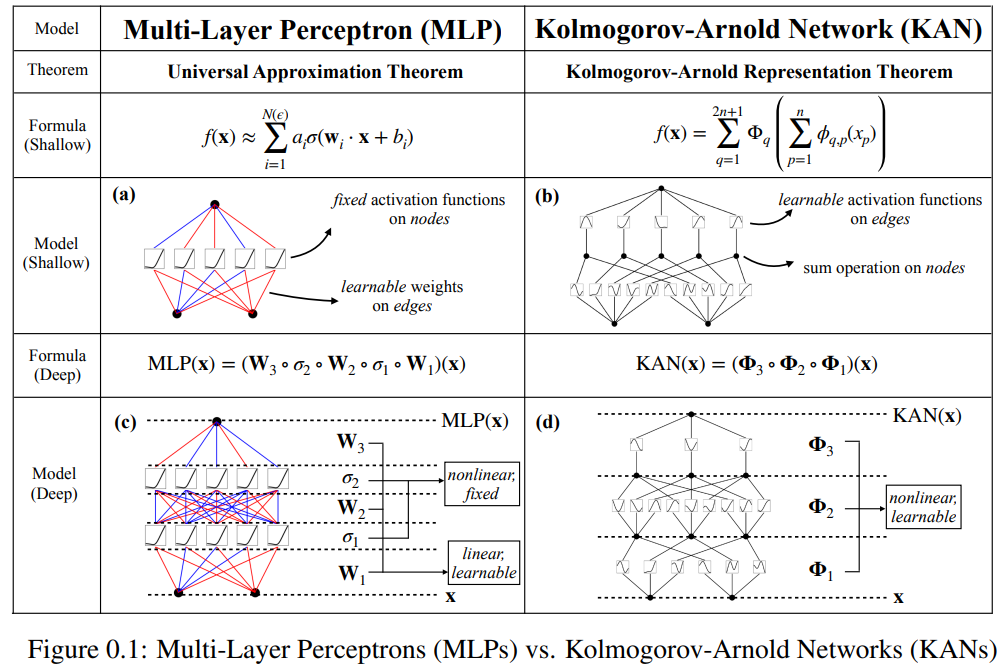
Dieses Papier schlägt eine vielversprechende Alternative zu mehrschichtigen Perzeptronen (MLPs) namens Kolmogorov-Arnold Networks (KAN) vor. Das Design von MLP ist vom universellen Approximationssatz inspiriert, während das Design von KAN vom Kolmogorov-Arnold-Darstellungssatz inspiriert ist. Ähnlich wie MLP verfügt KAN über eine vollständig vernetzte Struktur. Während MLP feste Aktivierungsfunktionen auf Knoten (Neuronen) platziert, platziert KAN lernbare Aktivierungsfunktionen auf Kanten (Gewichte), wie in Abbildung 0.1 dargestellt. Daher verfügt KAN überhaupt über keine lineare Gewichtsmatrix: Jeder Gewichtsparameter wird durch eine lernbare eindimensionale Funktion ersetzt, die als Spline parametrisiert ist. Die Knoten von KAN summieren einfach die eingehenden Signale, ohne eine nichtlineare Transformation anzuwenden.
Einige Leute befürchten möglicherweise, dass die Kosten für KAN zu hoch sind, da die Gewichtsparameter jedes MLP zur Spline-Funktion von KAN werden. Allerdings ermöglicht KAN einen viel kleineren Rechengraphen als MLP. Beispielsweise demonstrierten die Forscher eine PED-Lösung: Ein zweischichtiges KAN mit einer Breite von 10 ist 100-mal genauer als ein vierschichtiges MLP mit einer Breite von 100 (MSE sind 10^-7 bzw. 10^-5). Außerdem ist die Parametereffizienz um das Hundertfache verbessert (die Anzahl der Parameter beträgt 10^2 bzw. 10^4).
Die Möglichkeit, den Darstellungssatz von Kolmogorov-Arnold zum Aufbau neuronaler Netze zu verwenden, wurde untersucht. Allerdings bleibt die meiste Arbeit bei der ursprünglichen Darstellung von Tiefe 2, Breite (2n + 1) hängen, und es gibt keine Möglichkeit, modernere Techniken (z. B. Backpropagation) zum Trainieren des Netzwerks zu nutzen. Der Beitrag dieses Artikels besteht darin, die ursprüngliche Kolmogorov-Arnold-Darstellung auf beliebige Breite und Tiefe zu verallgemeinern und sie im heutigen Deep-Learning-Bereich wiederzubeleben, während gleichzeitig eine große Anzahl empirischer Experimente verwendet wird, um ihre potenzielle Rolle als Grundmodell von „KI +“ hervorzuheben Wissenschaft“, die von der Genauigkeit und Interpretierbarkeit des KAN profitiert.
Obwohl KAN über gute mathematische Erklärungsfähigkeiten verfügt, sind sie eigentlich nur eine Kombination aus Splines und MLP, die die Vorteile beider nutzt und deren Nachteile vermeidet. Splines sind bei niedrigdimensionalen Funktionen sehr genau, lassen sich leicht lokal anpassen und können zwischen verschiedenen Auflösungen wechseln. Da Splines jedoch keine kombinatorischen Strukturen nutzen können, leiden sie unter schwerwiegenden COD-Problemen. MLPs hingegen sind aufgrund ihrer Fähigkeit zum Lernen von Merkmalen weniger von COD betroffen, sind jedoch in niedrigdimensionalen Räumen nicht so genau wie Splines, da sie univariate Funktionen nicht optimieren können.
Um eine Funktion genau zu lernen, sollte das Modell nicht nur die kombinatorische Struktur (externe Freiheitsgrade) lernen, sondern auch die univariate Funktion (interne Freiheitsgrade) gut approximieren. KANs sind solche Modelle, weil sie äußerlich MLPs und innen Splines ähneln. Dadurch kann KAN nicht nur Features lernen (dank ihrer externen Ähnlichkeit mit MLPs), sondern diese gelernten Features auch mit sehr hoher Genauigkeit optimieren (dank ihrer internen Ähnlichkeit mit Splines).
Zum Beispiel für eine hochdimensionale Funktion:
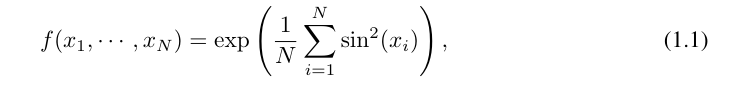
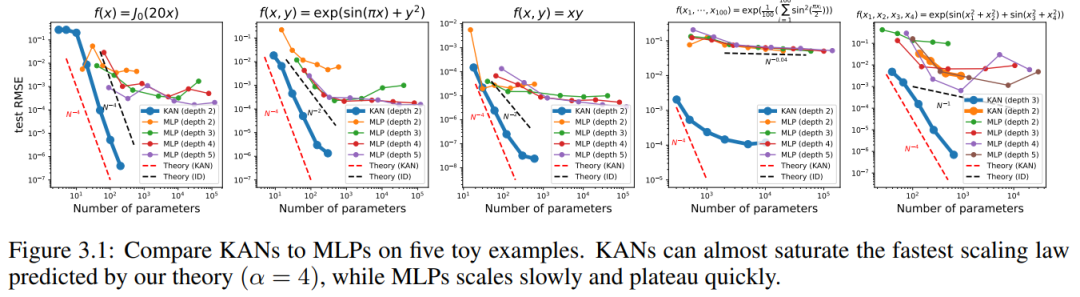
Wenn N groß ist, schlägt der Spline aufgrund von COD fehl; obwohl es für MLP möglich ist, eine verallgemeinerte additive Struktur zu lernen, verwendet es beispielsweise a Die ReLU-Aktivierungsfunktion zur Approximation der Exponential- und Sinusfunktionen ist sehr ineffizient. Im Gegensatz dazu ist KAN in der Lage, kombinatorische Strukturen und univariate Funktionen sehr gut zu lernen und übertrifft damit MLP deutlich (siehe Abbildung 3.1).
In diesem Artikel zeigen die Forscher eine große Anzahl experimenteller Werte, die KANs signifikante Verbesserung des MLP in Bezug auf Genauigkeit und Interpretierbarkeit widerspiegeln. Der Aufbau des Papiers ist in Abbildung 2.1 unten dargestellt. Der Code ist unter https://github.com/KindXiaoming/pykan verfügbar und kann auch über pip install pykan installiert werden.
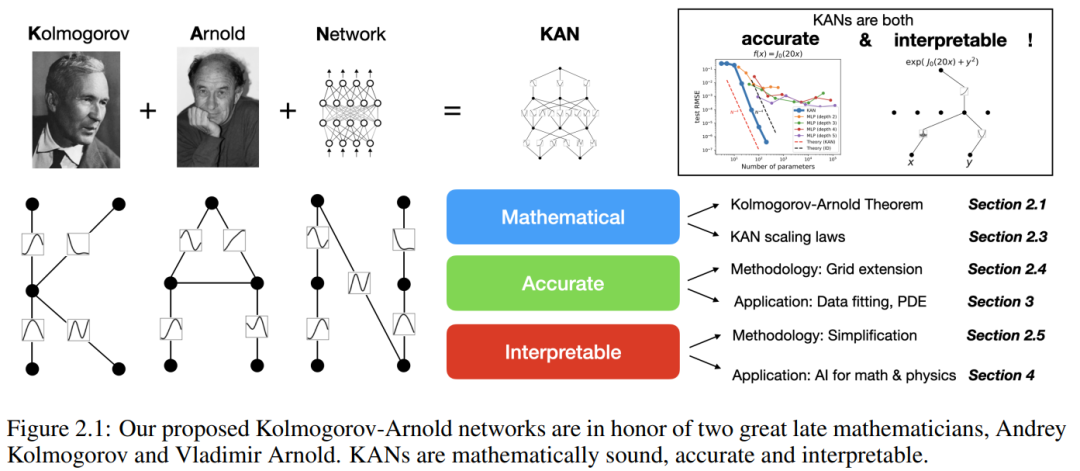
Kolmogorov-Arnold-Netzwerk (KAN)
Kolmogorov-Arnold-Darstellungssatz
Vladimir Arnold und Andrey Kolmogorov haben bewiesen, dass f geschrieben werden kann als: eine endliche Kombination einer kontinuierlichen Funktion mit einer Variablen und binären Additionsoperationen. Genauer gesagt kann eine glatte Funktion f: [0, 1]^n → R ausgedrückt werden als: Andere Funktionen können durch Einzelvariablenfunktionen und Summationen dargestellt werden. Man könnte meinen, dass dies eine gute Nachricht für maschinelles Lernen ist: Das Erlernen einer hochdimensionalen Funktion läuft darauf hinaus, eine eindimensionale Funktion in Polynomgrößen zu lernen. Diese eindimensionalen Funktionen können jedoch nicht glatt oder sogar fraktal sein und daher in der Praxis möglicherweise nicht erlernt werden. Der Kolmogorov-Arnold-Darstellungssatz ist daher im Wesentlichen ein Todesurteil im maschinellen Lernen, das als theoretisch korrekt, aber praktisch nutzlos angesehen wird.
Die Forscher sind jedoch optimistischer, was die Praktikabilität des Kolmogorov-Arnold-Theorems beim maschinellen Lernen angeht. Erstens besteht keine Notwendigkeit, bei der ursprünglichen Gleichung zu bleiben, die nur zwei Schichten der Nichtlinearität und eine kleine Anzahl von Termen (2n + 1) in einer verborgenen Schicht aufweist: Der Forscher wird das Netzwerk auf beliebige Breiten und Tiefen verallgemeinern. Zweitens sind die meisten Funktionen in der Wissenschaft und im täglichen Leben normalerweise glatt und weisen spärliche kombinatorische Strukturen auf, was glatte Kolmogorov-Arnold-Darstellungen erleichtern kann. 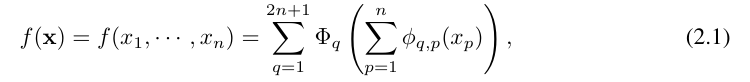
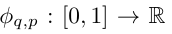
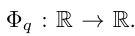 KAN-Architektur
KAN-Architektur
Angenommen, es gibt eine überwachte Lernaufgabe, die aus Eingabe- und Ausgabepaaren {x_i, y_i} besteht, und der Forscher hofft, eine Funktion f zu finden, so dass y_i ≈ f (x_i) für alle Datenpunkte gilt. Gleichung (2.1) bedeutet, dass die Aufgabe erfüllt ist, wenn die geeigneten Einzelvariablenfunktionen 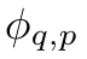 und
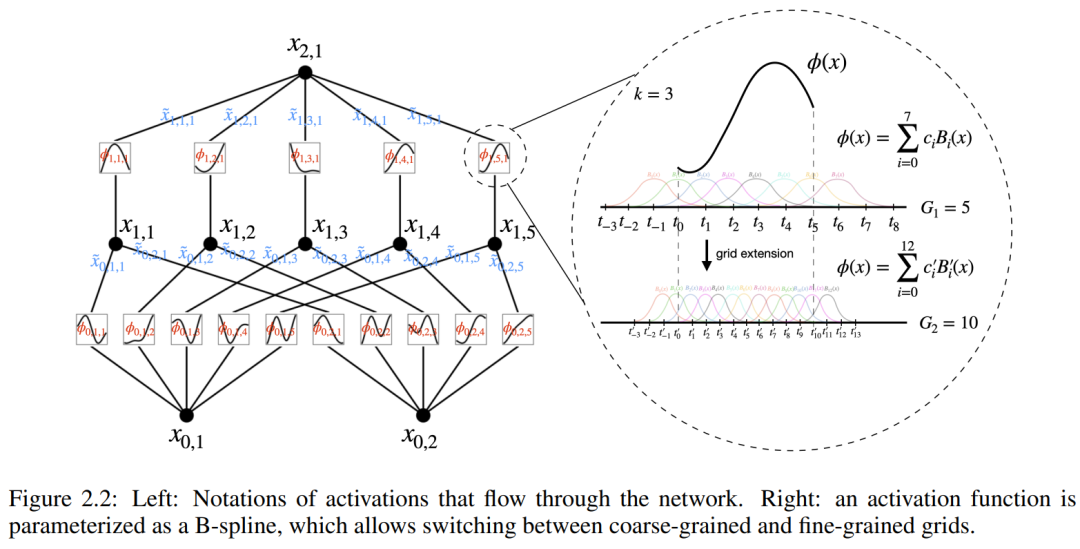
und 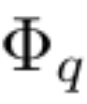 gefunden werden können. Dies inspiriert Forscher dazu, ein neuronales Netzwerk zu entwerfen, das Gleichung (2.1) explizit parametrisiert. Da alle zu lernenden Funktionen univariate Funktionen sind, parametrisiert der Forscher jede eindimensionale Funktion als B-Spline-Kurve mit lernbaren Koeffizienten lokaler B-Spline-Basisfunktionen (siehe rechte Seite von Abbildung 2.2). Wir haben jetzt einen Prototyp von KAN, dessen Rechendiagramm vollständig durch Gleichung (2.1) spezifiziert und in Abbildung 0.1(b) dargestellt ist (Eingabedimension n = 2), der wie ein zweischichtiges neuronales Netzwerk aussieht, auf dem Aktivierungsfunktionen platziert sind Kanten anstelle von Knoten (eine einfache Summierung wird an Knoten durchgeführt), und die Breite der mittleren Schicht beträgt 2n + 1.
gefunden werden können. Dies inspiriert Forscher dazu, ein neuronales Netzwerk zu entwerfen, das Gleichung (2.1) explizit parametrisiert. Da alle zu lernenden Funktionen univariate Funktionen sind, parametrisiert der Forscher jede eindimensionale Funktion als B-Spline-Kurve mit lernbaren Koeffizienten lokaler B-Spline-Basisfunktionen (siehe rechte Seite von Abbildung 2.2). Wir haben jetzt einen Prototyp von KAN, dessen Rechendiagramm vollständig durch Gleichung (2.1) spezifiziert und in Abbildung 0.1(b) dargestellt ist (Eingabedimension n = 2), der wie ein zweischichtiges neuronales Netzwerk aussieht, auf dem Aktivierungsfunktionen platziert sind Kanten anstelle von Knoten (eine einfache Summierung wird an Knoten durchgeführt), und die Breite der mittleren Schicht beträgt 2n + 1.
Wie bereits erwähnt, werden solche Netzwerke in der Praxis als zu einfach angesehen, um irgendeine Funktion mit Glättungssplines mit beliebiger Genauigkeit anzunähern. Daher verallgemeinern Forscher KAN auf breitere und tiefere Netzwerke. Da die Kolmogorov-Arnold-Darstellung einem zweischichtigen KAN entspricht, ist nicht klar, wie das KAN tiefer gemacht werden kann.
Der Durchbruch ist, dass die Forscher die Analogie zwischen MLP und KAN bemerkt haben. Sobald in MLP eine Schicht (bestehend aus linearen Transformationen und Nichtlinearitäten) definiert ist, können weitere Schichten gestapelt werden, um das Netzwerk tiefer zu machen. Um ein tiefes KAN aufzubauen, sollten Sie zunächst antworten: „Was ist eine KAN-Schicht?“ Forscher haben herausgefunden, dass eine KAN-Schicht mit n_in-dimensionaler Eingabe und n_out-dimensionaler Ausgabe als eindimensionale Funktionsmatrix definiert werden kann.
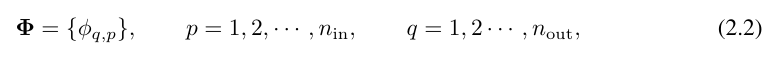
wobei die Funktion  trainierbare Parameter hat, wie unten beschrieben. Im Kolmogorov-Arnold-Theorem bilden die inneren Funktionen eine KAN-Schicht mit n_in = n und n_out = 2n+1, und die äußeren Funktionen bilden eine KAN-Schicht mit n_in = 2n + 1 und n_out = 1. Daher ist die Kolmogorov-Arnold-Darstellung in Gleichung (2.1) einfach eine Kombination aus zwei KAN-Schichten. Eine tiefere Kolmogorov-Arnold-Darstellung bedeutet nun: Stapeln Sie einfach mehr KAN-Schichten!
trainierbare Parameter hat, wie unten beschrieben. Im Kolmogorov-Arnold-Theorem bilden die inneren Funktionen eine KAN-Schicht mit n_in = n und n_out = 2n+1, und die äußeren Funktionen bilden eine KAN-Schicht mit n_in = 2n + 1 und n_out = 1. Daher ist die Kolmogorov-Arnold-Darstellung in Gleichung (2.1) einfach eine Kombination aus zwei KAN-Schichten. Eine tiefere Kolmogorov-Arnold-Darstellung bedeutet nun: Stapeln Sie einfach mehr KAN-Schichten!
Für ein besseres Verständnis ist die Einführung einiger Symbole erforderlich. Konkrete Beispiele und ein intuitives Verständnis finden Sie in Abbildung 2.2 (links). Die Form von KAN wird durch ein ganzzahliges Array dargestellt:

wobei n_i die Anzahl der Knoten in der i-ten Schicht des Rechendiagramms ist. Hier repräsentiert (l, i) das i-te Neuron der l-ten Schicht und x_l,i repräsentiert den Aktivierungswert des (l, i)-Neurons. Zwischen der l-ten Schicht und der l + 1-ten Schicht gibt es n_l*n_l+1 Aktivierungsfunktionen: Die Aktivierungsfunktion, die (l, j) und (l + 1, i) verbindet, wird ausgedrückt als

Funktion ϕ_l, The Der Voraktivierungswert von i,j wird einfach ausgedrückt als x_l,i; der Nachaktivierungswert von ϕ_l,i,j ist 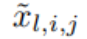 ≡ ϕ_l,i,j (x_l,i). Der Aktivierungswert des (l + 1, j)-ten Neurons ist die Summe aller eingehenden Aktivierungswerte:
≡ ϕ_l,i,j (x_l,i). Der Aktivierungswert des (l + 1, j)-ten Neurons ist die Summe aller eingehenden Aktivierungswerte:
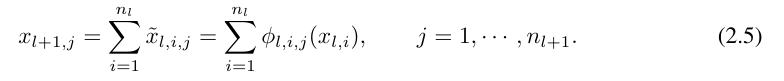
ausgedrückt in Matrixform wie folgt:

wobei Φ_l die KAN-Schicht ist, die dem entspricht Funktionsmatrix der l-ten Schicht. Ein allgemeines KAN-Netzwerk ist eine Kombination von L Schichten: Bei einem gegebenen Eingabevektor x_0 ∈ R^n0 ist die Ausgabe von KAN
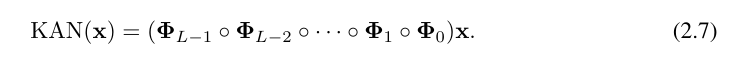
Die obige Gleichung kann auch in einer Situation ähnlich der Gleichung (2.1) geschrieben werden, vorausgesetzt, dass die Ausgabedimension n_L = 1 und definieren f (x) ≡ KAN (x):
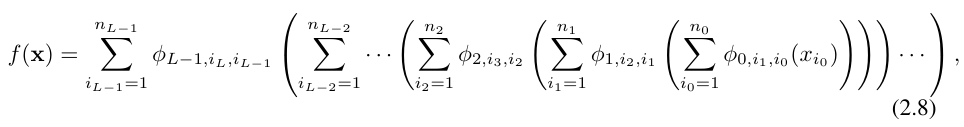
So zu schreiben ist ziemlich mühsam. Im Gegensatz dazu sind die Abstraktion der KAN-Schicht und ihre Visualisierung durch die Forscher prägnanter und intuitiver. Die ursprüngliche Kolmogorov-Arnold-Darstellung (2.1) entspricht einem zweischichtigen KAN der Form [n, 2n + 1, 1]. Beachten Sie, dass alle Operationen differenzierbar sind, sodass KAN mit Backpropagation trainiert werden kann. Zum Vergleich kann MLP als Verflechtung von affiner Transformation W und nichtlinearem σ geschrieben werden:
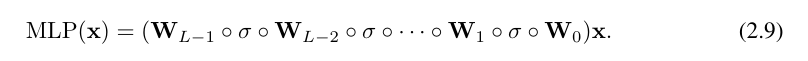
Offensichtlich verarbeitet MLP lineare Transformationen und Nichtlinearitäten als W bzw. σ, während KAN sie zusammen als Φ verarbeitet. In Abbildung 0.1 (c) und (d) zeigen die Forscher dreischichtiges MLP und dreischichtiges KAN, um den Unterschied zwischen ihnen zu veranschaulichen.
Genauigkeit von KAN
In der Arbeit zeigten die Autoren auch, dass KAN bei der Darstellung von Funktionen in verschiedenen Aufgaben (Regression und Lösung partieller Differentialgleichungen) effektiver als MLP ist. Und sie zeigen auch, dass KAN auf natürliche Weise beim kontinuierlichen Lernen ohne katastrophales Vergessen funktionieren kann.
Spielzeugdatensatz
Wir zeichnen den Test-RMSE von KAN und MLP als Funktion der Anzahl der Parameter in Abbildung 3.1 auf und zeigen, dass KAN bessere Skalierungskurven als MLP aufweist, insbesondere in hochdimensionalen Beispielen. Zum Vergleich zeichnen die Autoren die gemäß ihrer KAN-Theorie vorhergesagte Linie als rote gestrichelte Linie (α = k + 1 = 4) und die gemäß Sharma & Kaplan [17] vorhergesagte Linie als schwarze gestrichelte Linie (α) ein = (k + 1 )/d = 4/d). KAN kann die steilere rote Linie fast ausfüllen, während MLP sogar Schwierigkeiten hat, sich der Geschwindigkeit der langsameren schwarzen Linie anzunähern und schnell ein Plateau erreicht. Die Autoren stellen außerdem fest, dass im letzten Beispiel das zweischichtige KAN deutlich schlechter abschneidet als das dreischichtige KAN (Form [4, 2, 2, 1]). Dies unterstreicht, dass tiefere KANs ausdrucksstärker sind, und das Gleiche gilt auch für MLPs: Tiefere MLPs sind ausdrucksvoller als flachere MLPs.
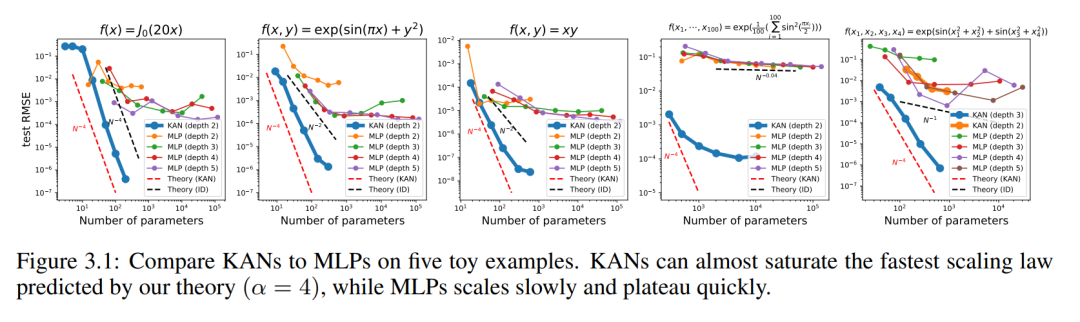
Sonderfunktionen
In diesem Abschnitt zeigen wir die folgenden zwei Punkte:
(1) Es ist möglich, (annähernd) kompakte KA-Darstellungen von Sonderfunktionen zu finden, was aus der Sicht von Kolmogorov offenbart wird. Arnold-Darstellung Neue mathematische Eigenschaften spezieller Funktionen.
(2) KAN ist bei der Darstellung spezieller Funktionen effizienter und genauer als MLP.
Für jeden Datensatz und jede Modellfamilie (KAN oder MLP) haben die Autoren die Pareto-Grenze auf der Anzahl der Parameter und der RMSE-Ebene aufgetragen, wie in Abbildung 3.2 dargestellt.
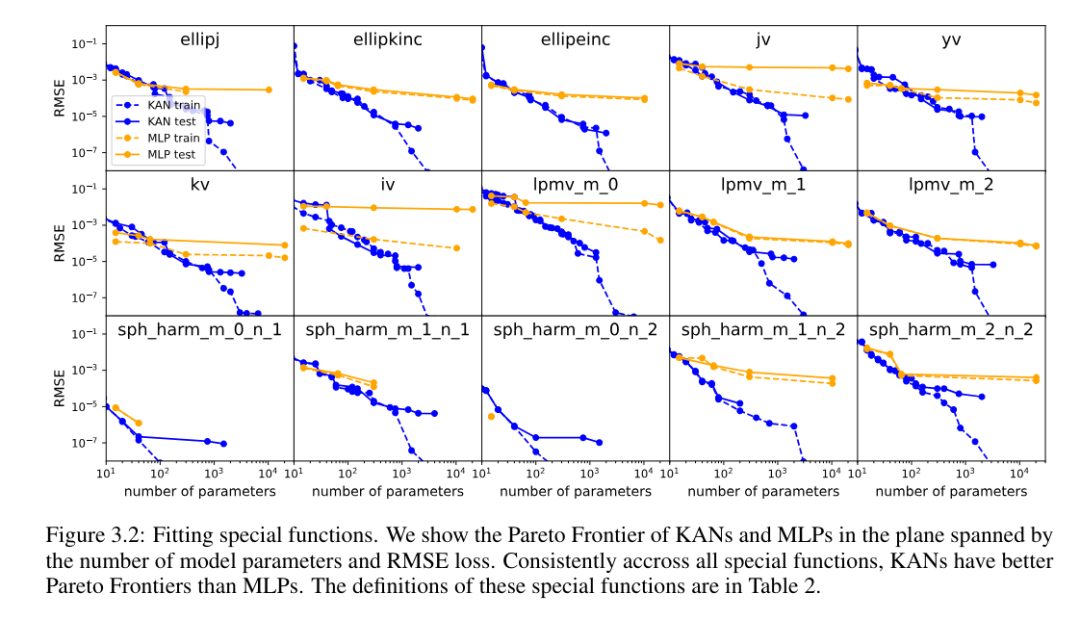
KAN schneidet durchweg besser ab als MLP, d. h. bei gleicher Parameteranzahl kann KAN geringere Trainings-/Testverluste als MLP erzielen. Darüber hinaus berichten die Autoren in Tabelle 2 über die (überraschend kompakte) Form des KAN für die von ihnen automatisch entdeckte Sonderfunktion. Einerseits ist es interessant, die Bedeutung dieser kompakten Darstellungen mathematisch zu erklären. Andererseits bedeuten diese kompakten Darstellungen, dass es möglich ist, eine hochdimensionale Nachschlagetabelle in mehrere eindimensionale Nachschlagetabellen zu zerlegen, was möglicherweise viel Speicher auf Kosten der Durchführung einiger Additionsoperationen zur Inferenzzeit (fast) einsparen kann unerheblich) .
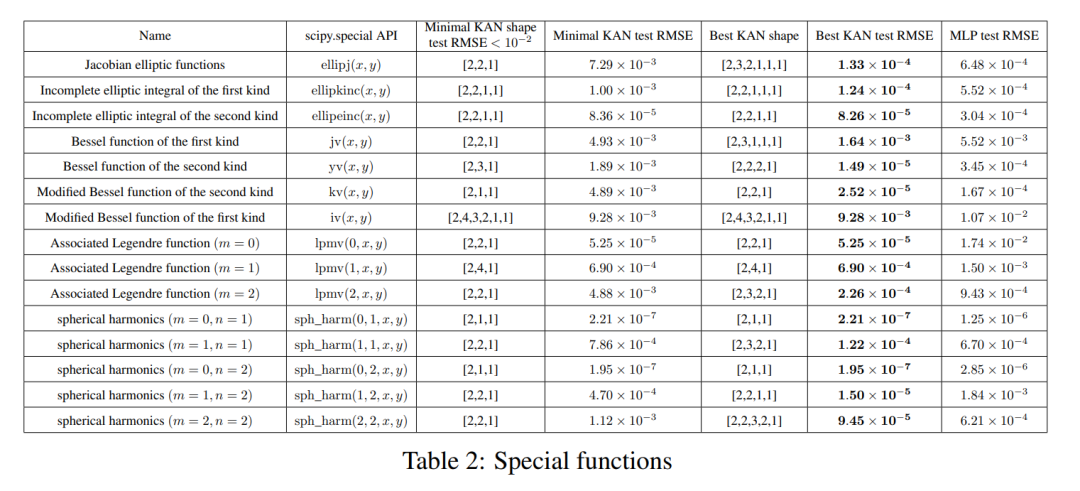
Feynman-Datensatz
Die Einstellung im vorherigen Abschnitt ist, dass wir die „echte“ KAN-Form eindeutig kennen. Der Grundgedanke im vorherigen Abschnitt ist, dass wir die „echte“ KAN-Form offensichtlich nicht kennen. In diesem Abschnitt wird eine Zwischensituation untersucht: Angesichts der Struktur des Datensatzes können wir KANs möglicherweise manuell erstellen, sind uns jedoch nicht sicher, ob sie optimal sind.
Für jede Hyperparameterkombination hat der Autor 3 zufällige Seeds ausprobiert. Für jeden Datensatz (Gleichung) und jede Methode geben sie in Tabelle 3 die Ergebnisse des besten Modells (minimale KAN-Form oder geringster Testverlust) bei zufälligen Startwerten und Tiefen an.
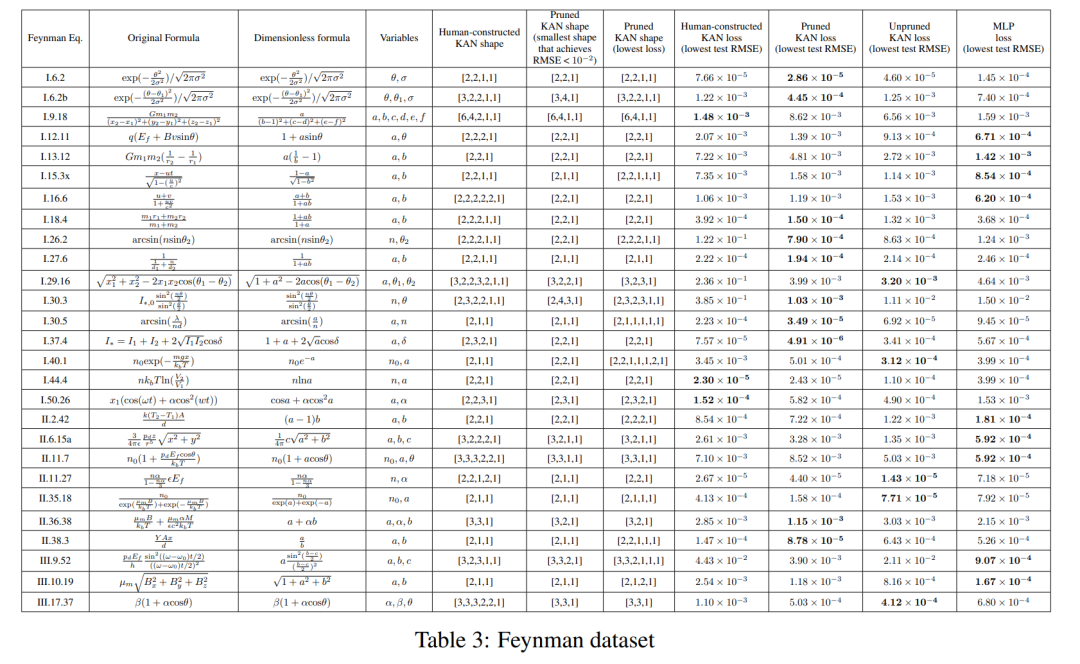
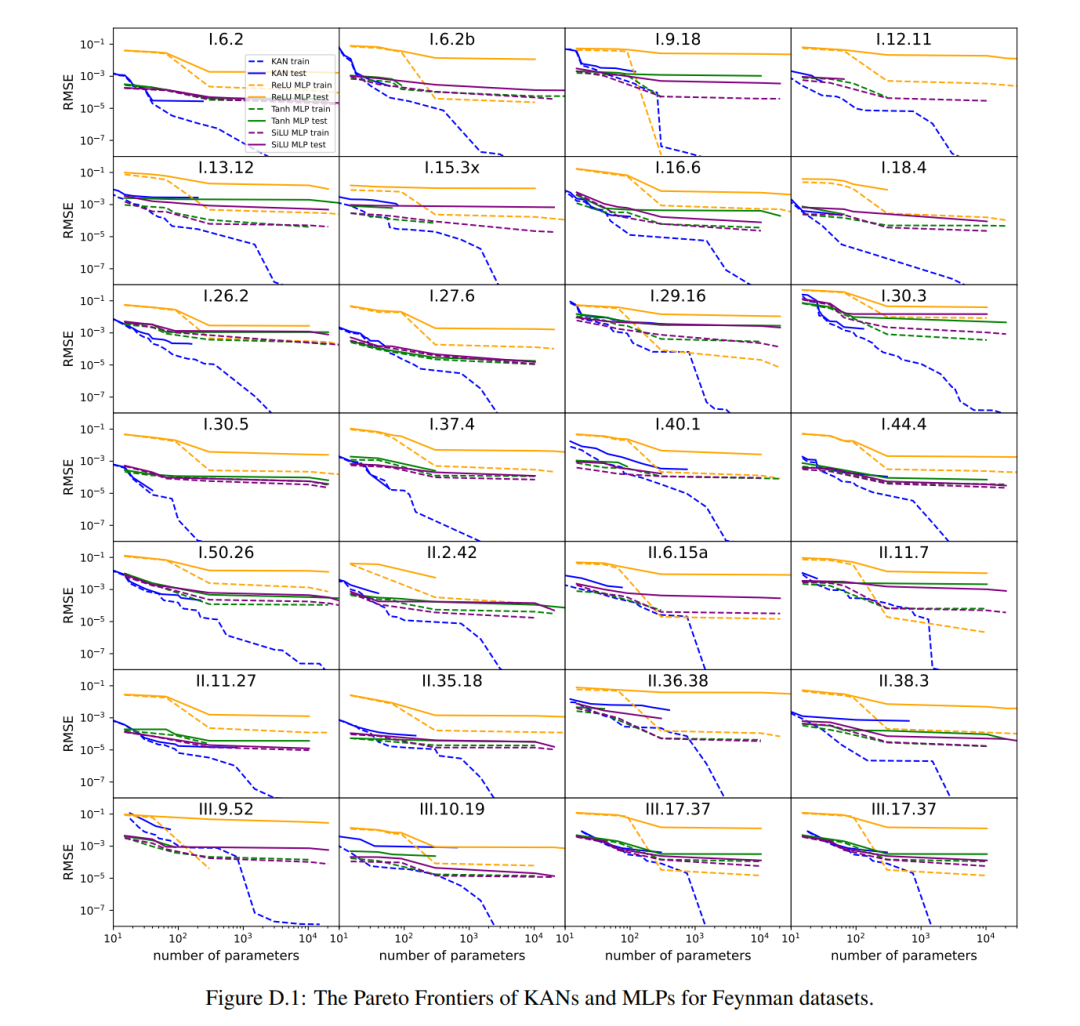
Sie fanden heraus, dass MLP und KAN im Durchschnitt gleich gut abschneiden. Für jeden Datensatz und jede Modellfamilie (KAN oder MLP) haben die Autoren die Pareto-Grenze auf der Ebene aufgetragen, die durch die Anzahl der Parameter und den RMSE-Verlust gebildet wird, wie in Abbildung D.1 dargestellt. Sie spekulieren, dass der Feynman-Datensatz zu einfach ist, um weitere Verbesserungen durch KAN zu ermöglichen, in dem Sinne, dass variable Abhängigkeiten oft glatt oder monoton sind, im Gegensatz zur Komplexität spezieller Funktionen, die oft oszillierendes Verhalten zeigen.
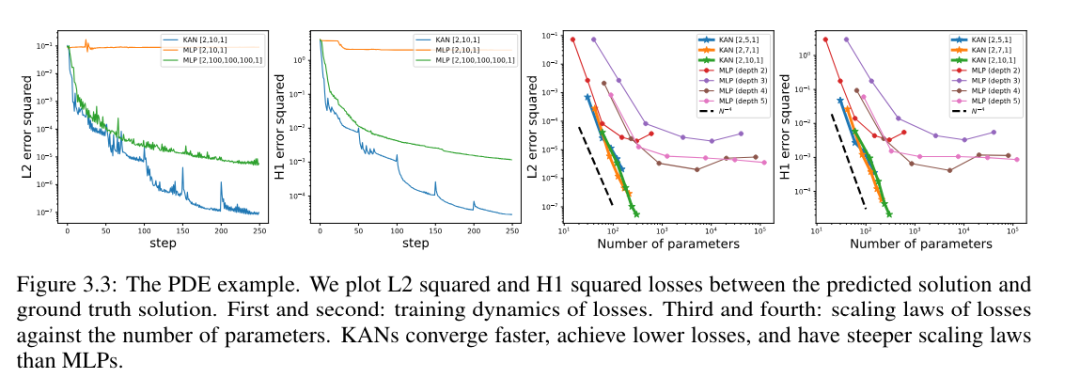
Partielle Differentialgleichungen lösen
Der Autor verglich KAN- und MLP-Architekturen mit denselben Hyperparametern. Sie maßen den Fehler in der L^2-Norm und der Energienorm (H^1) und beobachteten, dass KAN ein besseres Skalierungsgesetz und einen kleineren Fehler erreichte, während es ein kleineres Netzwerk und weniger Parameter verwendete, siehe Abbildung 3.3. Daher spekulierten sie, dass KAN das Potenzial haben könnte, als gute neuronale Netzwerkdarstellung für die Modellreduktion partieller Differentialgleichungen (PDE) zu dienen.
Kontinuierliches Lernen
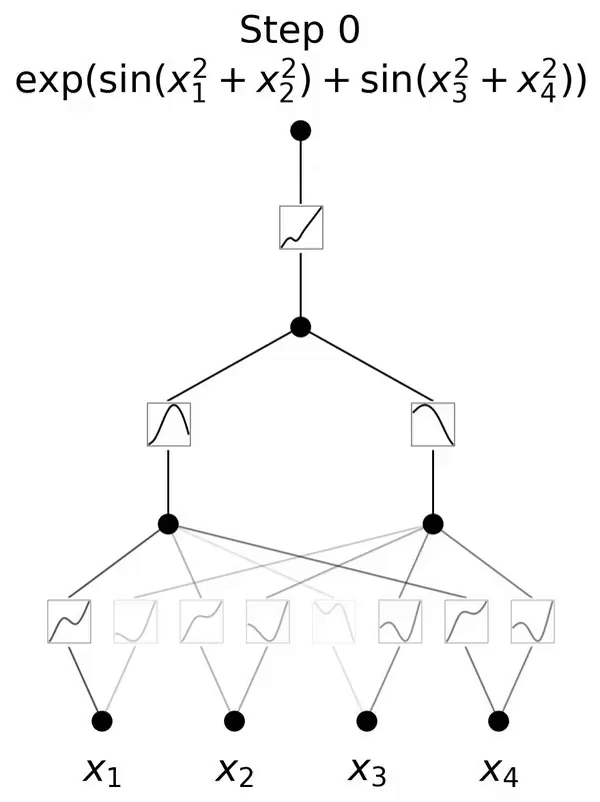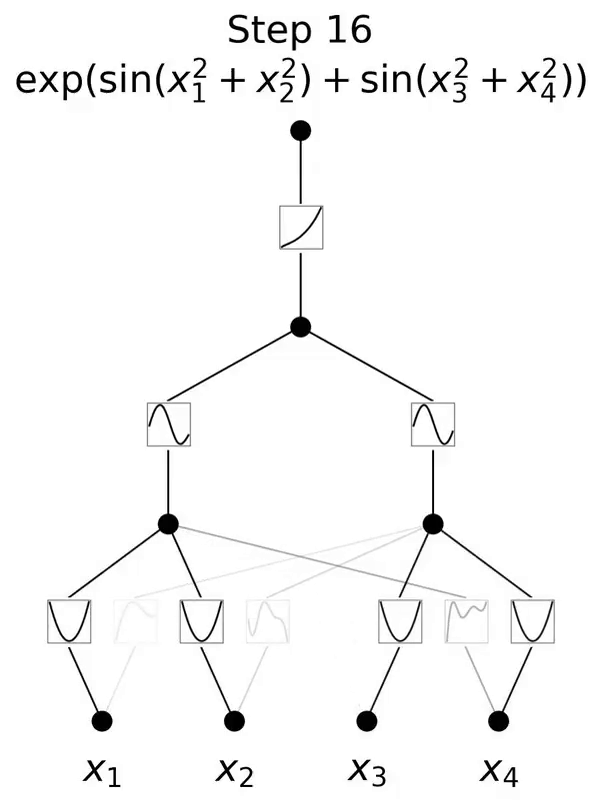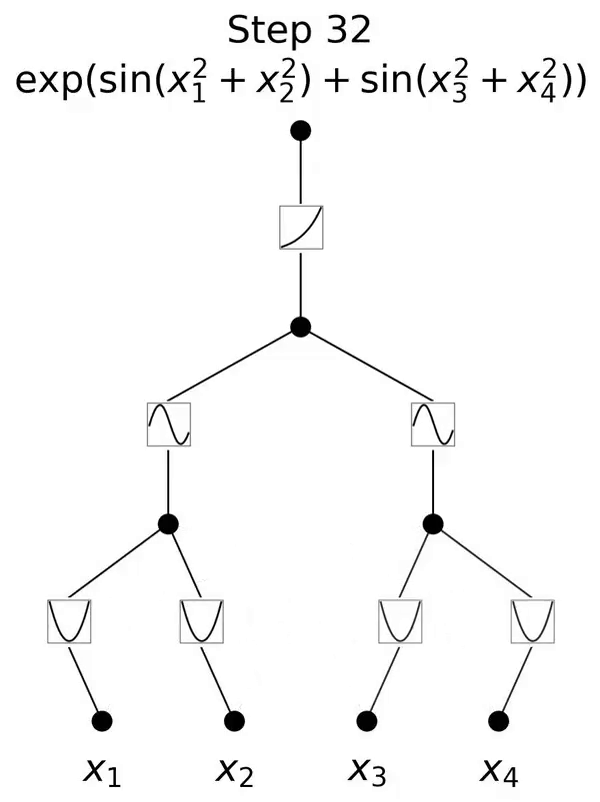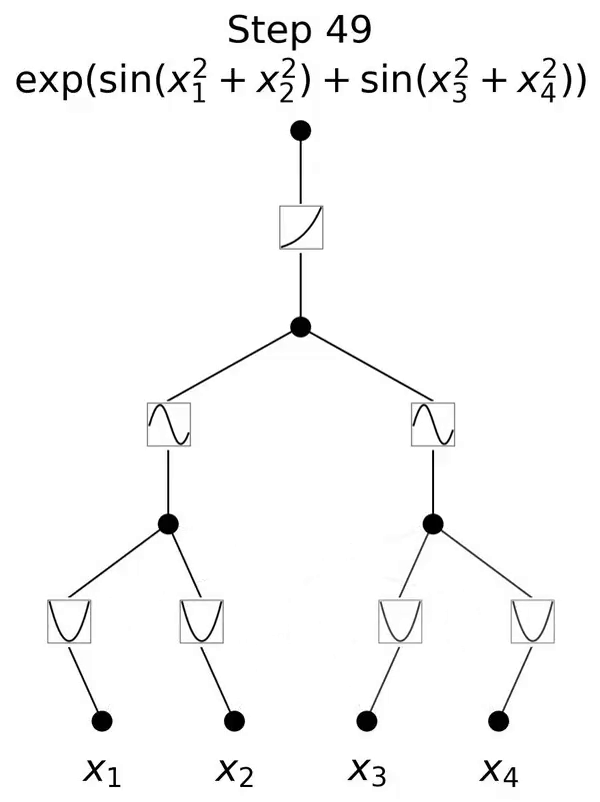
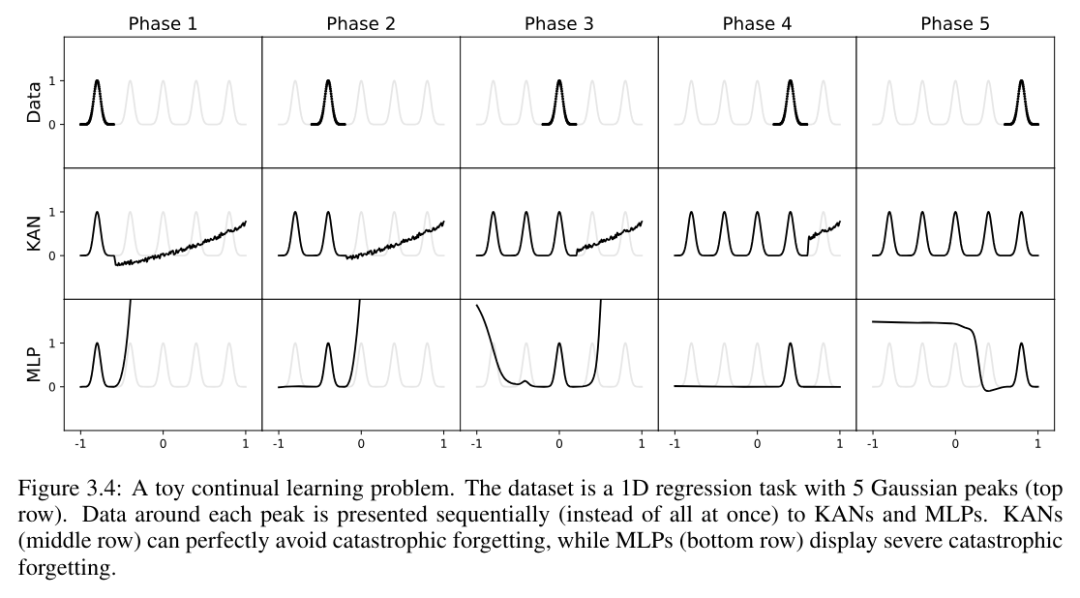
Die Autoren zeigen, dass KAN lokale Plastizität aufweist und katastrophales Vergessen vermeiden kann, indem es die Lokalität von Splines ausnutzt. Die Idee ist einfach: Da die Spline-Basis lokal ist, wirkt sich eine Stichprobe nur auf einige nahegelegene Spline-Koeffizienten aus, während die entfernten Koeffizienten unverändert bleiben (das ist es, was wir wollen, da die entfernten Regionen möglicherweise bereits die Koeffizienten speichern, die wir beibehalten möchten). . Da MLP im Gegensatz dazu normalerweise globale Aktivierungsfunktionen wie ReLU/Tanh/SiLU usw. verwendet, können sich lokale Änderungen unkontrolliert in entfernte Regionen ausbreiten und die dort gespeicherten Informationen zerstören.
Der Autor verifiziert diese Intuition anhand eines einfachen Beispiels. Eine eindimensionale Regressionsaufgabe besteht aus 5 Gaußschen Peaks. Die Daten um jeden Peak herum werden der Reihe nach (und nicht alle auf einmal) dargestellt, wie in der oberen Zeile von Abbildung 3.4 dargestellt, getrennt für KAN und MLP. Die Vorhersageergebnisse von KAN und MLP nach jeder Trainingsphase werden in der mittleren bzw. unteren Zeile angezeigt. Wie erwartet rekonstruiert KAN nur Regionen, in denen zum aktuellen Zeitpunkt Daten vorhanden sind, und lässt vorherige Regionen unverändert. Im Gegensatz dazu rekonstruiert MLP die gesamte Region, nachdem es eine neue Datenprobe gesehen hat, was zu katastrophalem Vergessen führt.
KAN ist interpretierbar
In Kapitel 4 des Artikels zeigen die Autoren, dass KAN dank der in Abschnitt 2.5 entwickelten Techniken interpretierbar und interaktiv ist. Sie wollten die Anwendung von KAN nicht nur bei Syntheseaufgaben (Abschn. 4.1 und 4.2), sondern auch in der realen wissenschaftlichen Forschung testen. Sie zeigen, dass KANs in der Lage sind, komplexe Beziehungen in der Übergangstheorie (Abschnitt 4.3) und Phasenübergangsgrenzen in der Physik der kondensierten Materie (Abschnitt 4.4) (wieder)zuentdecken. Aufgrund seiner Genauigkeit und Interpretierbarkeit hat KAN das Potenzial, ein grundlegendes Modell für KI + Wissenschaft zu werden.
Diskussion
In dem Artikel diskutiert der Autor die Einschränkungen und zukünftigen Entwicklungsrichtungen von KAN aus der Perspektive mathematischer Grundlagen, Algorithmen und Anwendungen.
Mathematische Aspekte: Obwohl der Autor eine vorläufige mathematische Analyse von KANs durchgeführt hat (Theorem 2.1), ist ihr mathematisches Verständnis noch sehr begrenzt. Der Kolmogorov-Arnold-Darstellungssatz wurde mathematisch gründlich untersucht, entspricht jedoch einem KAN der Form [n, 2n + 1, 1], das eine sehr eingeschränkte Unterklasse von KAN darstellt. Bedeutet der empirische Erfolg bei tieferen KANs etwas mathematisch Grundlegendes? Ein attraktives verallgemeinertes Kolmogorov-Arnold-Theorem könnte „tiefere“ Kolmogorov-Arnold-Darstellungen definieren, die über die Kombination zweier Schichten hinausgehen, und möglicherweise die Glätte der Aktivierungsfunktion mit der Tiefe in Beziehung setzen. Angenommen, es gibt Funktionen, die in der ursprünglichen Kolmogorov-Arnold-Darstellung (Tiefe 2) nicht glatt dargestellt werden können, aber in Tiefe 3 oder tiefer glatt dargestellt werden können. Können wir dieses Konzept der „Kolmogorov-Arnold-Tiefe“ verwenden, um Funktionsklassen zu charakterisieren?
Algorithmusmäßig besprachen sie folgende Punkte:
Genauigkeit. Beim Architekturdesign und beim Training gibt es mehrere Optionen, die noch nicht vollständig untersucht wurden. Daher gibt es möglicherweise Alternativen zur weiteren Verbesserung der Genauigkeit. Beispielsweise könnte die Spline-Aktivierungsfunktion durch radiale Basisfunktionen oder andere lokale Kernelfunktionen ersetzt werden. Adaptive Grid-Strategien können eingesetzt werden.
Effizienz. Einer der Hauptgründe, warum KAN langsam ist, liegt darin, dass verschiedene Aktivierungsfunktionen die Vorteile der Stapelberechnung (große Datenmengen, die über dieselbe Funktion geleitet werden) nicht nutzen können. Tatsächlich können wir zwischen MLP (alle Aktivierungsfunktionen sind gleich) und KAN (alle Aktivierungsfunktionen sind unterschiedlich) interpolieren, indem wir die Aktivierungsfunktionen in Gruppen („Vielfache“) gruppieren, wobei die Mitglieder der Gruppe dieselbe Aktivierungsfunktion teilen.
Eine Mischung aus KAN und MLP. Im Vergleich zu MLP weist KAN zwei Hauptunterschiede auf:
(i) Die Aktivierungsfunktion befindet sich an den Kanten statt an Knoten.
(ii) Die Aktivierungsfunktion ist lernbar statt fest.
Welche Änderung erklärt die Vorteile von KAN besser? Die Autoren präsentieren ihre vorläufigen Ergebnisse in Anhang B, wo sie ein Modell mit (ii) untersuchen, d. h. die Aktivierungsfunktion ist lernbar (wie KAN), aber ohne (i), d. h. die Aktivierungsfunktion befindet sich an den Knoten (wie ein MLP). ). Darüber hinaus kann man ein weiteres Modell bauen, dessen Aktivierungsfunktion fest ist (wie MLP), sich aber an den Rändern befindet (wie KAN).
Anpassungsfähigkeit. Aufgrund der inhärenten Lokalität von Spline-Basisfunktionen können wir Adaptivität in den Entwurf und das Training von KANs einführen, um Genauigkeit und Effizienz zu verbessern: siehe [93, 94] für mehrstufige Trainingsideen wie Mehrgittermethoden oder domänenabhängige Basisfunktionen wie Multiskalenmethoden in [95].
Anwendungen: Die Autoren haben einige vorläufige Beweise dafür vorgelegt, dass KAN bei naturwissenschaftlichen Aufgaben wie der Anpassung physikalischer Gleichungen und der Lösung von PDEs effektiver ist als MLP. Sie gehen davon aus, dass KAN auch bei der Lösung der Navier-Stokes-Gleichungen, der Dichtefunktionaltheorie oder jeder anderen Aufgabe, die als Regressions- oder PDE-Lösung formuliert werden kann, vielversprechend sein könnte. Sie hoffen auch, KAN auf Aufgaben im Zusammenhang mit maschinellem Lernen anzuwenden, was die Integration von KAN in aktuelle Architekturen wie Transformatoren erfordern wird – man kann „Kansformer“ vorschlagen, um MLPs durch KAN in Transformatoren zu ersetzen.
KAN als Sprachmodelle für KI + Wissenschaft: Große Sprachmodelle sind transformativ, weil sie für jeden nützlich sind, der natürliche Sprache verwenden kann. Die Sprache der Wissenschaft sind Funktionen. KANs bestehen aus interpretierbaren Funktionen. Wenn ein menschlicher Benutzer also auf ein KAN starrt, ist es so, als würde er mit ihm über funktionale Sprache kommunizieren. Dieser Absatz soll das Paradigma der Zusammenarbeit zwischen KI und Wissenschaftlern hervorheben und nicht das spezifische Tool KAN. So wie Menschen verschiedene Sprachen zur Kommunikation nutzen, gehen die Autoren davon aus, dass KAN in Zukunft nur eine der Sprachen der KI + Wissenschaft sein wird, obwohl KAN eine der ersten Sprachen sein wird, die KI und Menschen dazu befähigt kommunizieren. Dank der Ermöglichung von KAN war das Paradigma der Zusammenarbeit zwischen KI und Wissenschaftlern jedoch nie einfacher und bequemer, was uns dazu veranlasst, zu überdenken, wie wir KI und Wissenschaft angehen wollen: Wollen wir KI-Wissenschaftler oder wollen wir KI, die Wissenschaftlern hilft? Eine inhärente Schwierigkeit für Wissenschaftler im Bereich der (vollautomatisierten) KI ist die Schwierigkeit, menschliche Präferenzen zu quantifizieren, wodurch menschliche Präferenzen in KI-Ziele kodifiziert würden. Tatsächlich haben Wissenschaftler auf verschiedenen Gebieten möglicherweise unterschiedliche Ansichten darüber, welche Funktionen einfach oder erklärbar sind. Daher ist es für Wissenschaftler vorzuziehen, über eine KI zu verfügen, die die Sprache der Wissenschaft (Funktionen) sprechen und problemlos mit den induktiven Vorurteilen einzelner Wissenschaftler interagieren kann, um sie an einen bestimmten wissenschaftlichen Bereich anzupassen.
Schlüsselfrage: KAN oder MLP?
Der größte Engpass von KAN ist derzeit die langsame Trainingsgeschwindigkeit. Bei gleicher Parameteranzahl beträgt die Trainingszeit von KAN normalerweise das Zehnfache der von MLP. Die Autoren geben an, dass sie sich ehrlich gesagt nicht darum bemüht haben, die Effizienz von KAN zu optimieren, und glauben daher, dass die langsame Trainingsgeschwindigkeit von KAN eher ein technisches Problem ist, das in Zukunft verbessert werden kann, als eine grundlegende Einschränkung. Wenn jemand ein Modell schnell trainieren möchte, sollte er MLP verwenden. In anderen Fällen sollten KANs jedoch genauso gut oder besser als MLPs sein, sodass sie einen Versuch wert sind. Der Entscheidungsbaum in Abbildung 6.1 kann bei der Entscheidung helfen, wann eine KAN verwendet werden soll. Kurz gesagt: Wenn Ihnen Interpretierbarkeit und/oder Genauigkeit wichtig sind und langsames Training kein großes Problem darstellt, empfiehlt der Autor, KAN auszuprobieren.
Für weitere Einzelheiten lesen Sie bitte das Originalpapier.
Das obige ist der detaillierte Inhalt vonTransformer will Kansformer werden? Es hat Jahrzehnte gedauert, bis MLP den Herausforderer KAN an die Spitze brachte. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1376
1376
 52
52
 Welche Bibliotheken werden für die Operationen der schwimmenden Punktzahl in Go verwendet?
Apr 02, 2025 pm 02:06 PM
Welche Bibliotheken werden für die Operationen der schwimmenden Punktzahl in Go verwendet?
Apr 02, 2025 pm 02:06 PM
In der Bibliothek, die für den Betrieb der Schwimmpunktnummer in der GO-Sprache verwendet wird, wird die Genauigkeit sichergestellt, wie die Genauigkeit ...
 Gitee Pages statische Website -Bereitstellung fehlgeschlagen: Wie können Sie einzelne Dateien 404 Fehler beheben und beheben?
Apr 04, 2025 pm 11:54 PM
Gitee Pages statische Website -Bereitstellung fehlgeschlagen: Wie können Sie einzelne Dateien 404 Fehler beheben und beheben?
Apr 04, 2025 pm 11:54 PM
GitePages statische Website -Bereitstellung fehlgeschlagen: 404 Fehlerbehebung und Auflösung bei der Verwendung von Gitee ...
 So führen Sie das H5 -Projekt aus
Apr 06, 2025 pm 12:21 PM
So führen Sie das H5 -Projekt aus
Apr 06, 2025 pm 12:21 PM
Ausführen des H5 -Projekts erfordert die folgenden Schritte: Installation der erforderlichen Tools wie Webserver, Node.js, Entwicklungstools usw. Erstellen Sie eine Entwicklungsumgebung, erstellen Sie Projektordner, initialisieren Sie Projekte und schreiben Sie Code. Starten Sie den Entwicklungsserver und führen Sie den Befehl mit der Befehlszeile aus. Vorschau des Projekts in Ihrem Browser und geben Sie die Entwicklungsserver -URL ein. Veröffentlichen Sie Projekte, optimieren Sie Code, stellen Sie Projekte bereit und richten Sie die Webserverkonfiguration ein.
 Welche Bibliotheken in GO werden von großen Unternehmen entwickelt oder von bekannten Open-Source-Projekten bereitgestellt?
Apr 02, 2025 pm 04:12 PM
Welche Bibliotheken in GO werden von großen Unternehmen entwickelt oder von bekannten Open-Source-Projekten bereitgestellt?
Apr 02, 2025 pm 04:12 PM
Welche Bibliotheken in GO werden von großen Unternehmen oder bekannten Open-Source-Projekten entwickelt? Bei der Programmierung in Go begegnen Entwickler häufig auf einige häufige Bedürfnisse, ...
 Wie gibt ich die mit dem Modell in Beego Orm zugeordnete Datenbank an?
Apr 02, 2025 pm 03:54 PM
Wie gibt ich die mit dem Modell in Beego Orm zugeordnete Datenbank an?
Apr 02, 2025 pm 03:54 PM
Wie kann man im Beegoorm -Framework die mit dem Modell zugeordnete Datenbank angeben? In vielen BeEGO -Projekten müssen mehrere Datenbanken gleichzeitig betrieben werden. Bei Verwendung von BeEGO ...
 Wie löste ich das Problem des Typs des user_id -Typs bei der Verwendung von Redis -Stream, um Nachrichtenwarteschlangen in GO -Sprache zu implementieren?
Apr 02, 2025 pm 04:54 PM
Wie löste ich das Problem des Typs des user_id -Typs bei der Verwendung von Redis -Stream, um Nachrichtenwarteschlangen in GO -Sprache zu implementieren?
Apr 02, 2025 pm 04:54 PM
Das Problem der Verwendung von RETISTREAM zur Implementierung von Nachrichtenwarteschlangen in der GO -Sprache besteht darin, die Go -Sprache und Redis zu verwenden ...
 Bedarf die Produktion von H5 -Seiten eine kontinuierliche Wartung?
Apr 05, 2025 pm 11:27 PM
Bedarf die Produktion von H5 -Seiten eine kontinuierliche Wartung?
Apr 05, 2025 pm 11:27 PM
Die H5 -Seite muss aufgrund von Faktoren wie Code -Schwachstellen, Browserkompatibilität, Leistungsoptimierung, Sicherheitsaktualisierungen und Verbesserungen der Benutzererfahrung kontinuierlich aufrechterhalten werden. Zu den effektiven Wartungsmethoden gehören das Erstellen eines vollständigen Testsystems, die Verwendung von Versionstools für Versionskontrolle, die regelmäßige Überwachung der Seitenleistung, das Sammeln von Benutzern und die Formulierung von Wartungsplänen.
 Wie erhalten Sie die Daten der Versandregion der Überseeversion? Was stehen einige vorgefertigte Ressourcen zur Verfügung?
Apr 01, 2025 am 08:15 AM
Wie erhalten Sie die Daten der Versandregion der Überseeversion? Was stehen einige vorgefertigte Ressourcen zur Verfügung?
Apr 01, 2025 am 08:15 AM
Frage Beschreibung: Wie erhalten Sie die Daten der Versandregion der Überseeversion? Gibt es bereitgestellte Ressourcen? Werden Sie im grenzüberschreitenden E-Commerce oder im globalisierten Geschäft genau ...



