Das Aufkommen kleiner Sprachmodelle soll die Nachteile des teuren Trainings und der Inferenz großer Sprachmodelle ausgleichen, hat aber auch die Tatsache, dass seine Leistung nach dem Training bis zu einem bestimmten Grad abnimmt (Sättigungsphänomen), so der Grund denn dieses Phänomen ist Was? Kann es überwunden und genutzt werden, um die Leistung kleiner Sprachmodelle zu verbessern?
Der neueste Fortschritt auf dem Gebiet der Sprachmodellierung liegt im Vortraining hochparametrisierter neuronaler Netze auf extrem großen Webtextkorpora. In der Praxis kann die Verwendung eines solchen Modells für Training und Inferenz kostspielig sein und den Einsatz kleinerer alternativer Modelle erforderlich machen. Es wurde jedoch beobachtet, dass es bei kleineren Modellen zu einer Sättigung und einem Phänomen kommen kann, das durch einen Leistungsabfall und ein Plateau in einem fortgeschrittenen Trainingsstadium gekennzeichnet ist.
Ein kürzlich veröffentlichter Artikel ergab, dass dieses Sättigungssummenphänomen durch eine Diskrepanz zwischen der latenten Dimensionalität kleinerer Modelle und dem hohen Rang der Zielkontext-Wahrscheinlichkeitsverteilung erklärt werden kann. Diese Nichtübereinstimmung beeinträchtigt die Leistung der in diesen Modellen verwendeten linearen Vorhersageköpfe, indem sie den sogenannten Softmax-Engpass nutzt.
Link zum Papier: https://arxiv.org/pdf/2404.07647.pdf
Dieses Papier misst die Auswirkungen des Softmax-Engpasses unter verschiedenen Einstellungen und stellt fest, dass Modelle, die auf weniger als 1000 versteckten Dimensionen basieren, tendenziell vorgefertigt sind -Trainierte degenerierte latente Darstellungen werden zu einem späteren Zeitpunkt übernommen, was zu einer verringerten Bewertungsleistung führt.
Einführung
Das Problem der Darstellungsverschlechterung ist ein häufiges Phänomen, das verschiedene Modi betrifft, beispielsweise selbstüberwachte Lernmethoden für Textdaten. Beobachtungen von Zwischendarstellungen von Sprachmodellen zeigen deren geringe Winkelvariabilität (oder Anisotropie) oder ungewöhnliche Dimensionen, die während des Trainings auftreten. Diese Beobachtungen werden jedoch meist an relativ kleinen Modellen gemacht, deren Abmessungen mit Familienmodellen wie BERT oder GPT-2 vergleichbar sind.
Diese Modelle bestehen typischerweise aus einem neuronalen Netzwerk f_θ, das eine Folge von Token akzeptiert:
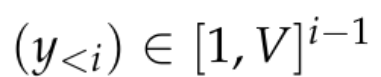
und eine relativ niedrigdimensionale Kontextdarstellung in R^d generiert, wobei d die verborgene Dimension des Modells ist. Anschließend verlassen sie sich auf einen Sprachmodellierungskopf, der den Logarithmus der Wahrscheinlichkeit des Kontexttokens erstellt. Eine häufige Wahl für einen Sprachmodellierungskopf ist eine lineare Schicht mit den Parametern W ∈ R^(V×d), wobei V die Anzahl der möglichen Token ist. Die resultierende Wahrscheinlichkeitsverteilung für den nächsten Token ist also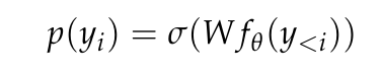 
wobei σ die Softmax-Funktion ist.
Im Bereich der Sprachmodellierung besteht der aktuelle Trend darin, die durch GPT-2 eingeführte generative Pre-Training-Methode zu erweitern, was bedeutet, neuronale Modelle, die aus Milliarden von Parametern bestehen, auf einem riesigen Webtextkorpus zu trainieren. Das Training und die Anwendung dieser stark parametrisierten Modelle wirft jedoch energie- und hardwarebezogene Probleme auf, weshalb Wege gefunden werden müssen, mit kleineren Modellen ähnliche Leistungsniveaus zu erreichen.
Die Auswertung der Pythia-Modellsuite zeigt jedoch, dass das Training kleiner Modelle auf sehr großen Korpora zu einer Sättigung führen kann, die sich in einem Leistungsabfall spät im Vortraining äußert. Dieser Artikel untersucht dieses Sättigungsphänomen durch die Linse der Repräsentationsverschlechterung und stellt fest, dass zwischen den beiden Phänomenen eine starke Korrelation besteht. Gleichzeitig wird weiter gezeigt, dass die Repräsentationsverschlechterung in den Sprachmodellierungsköpfen kleiner Modelle auftritt und sowohl theoretisch als auch empirisch nachgewiesen wurde zeigt, wie der Header der linearen Sprachmodellierung zu einem Leistungsengpass für Architekturen werden kann, die auf kleinen versteckten Dimensionen basieren.
Phänomen der Sprachmodellsättigung
In diesem Artikel wird zunächst bestätigt, dass die Leistungssättigung von Pythia-Kontrollpunkten tatsächlich beobachtet und quantifiziert werden kann, da es sich um die einzigen veröffentlichten Zwischenkontrollpunkte für eine Reihe von Modellgrößen handelt. Dieses Papier misst die Kreuzentropie von Pythia-Kontrollpunkten an 50.000 Token, die zufällig aus ihrem Datensatz vor dem Training (d. h. The Pile) entnommen wurden.
In Abbildung 1a ist deutlich zu erkennen, dass selbst das 410-Millionen-Parameter-Modell eine Sättigung erreicht, die sich in einem Anstieg des domäneninternen Verlusts in der fortgeschrittenen Trainingsphase äußert.
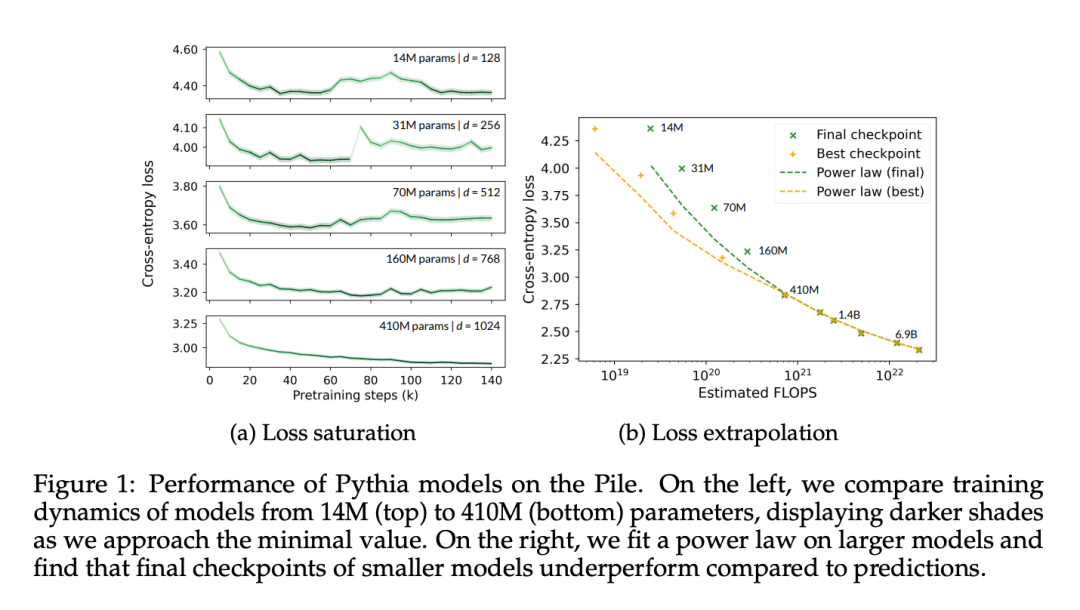
In Abbildung 1b passt dieser Artikel die Datenpunkte des Modells ausgehend von 410 Millionen Parametern gemäß der Methode von Hoffmann et al. (2022) an und optimiert nur die mit dem Modell verbundenen Konstanten (A und α). , Unter Wiederverwendung aller anderen Werte (B = 410,7, β = 0,28, E = 1,69). Hier überprüfen wir die von Hoffmann et al. (2022) angegebene Beziehung zwischen der Parameteranzahl N und der Tokenanzahl T:
In diesem Artikel wurde festgestellt, dass die optimalen Parameter A = 119,09 und α = 0,246 sind. Die Autoren zeigen angepasste Kurven der Token-Anzahl, die optimalen und endgültigen Kontrollpunkten entsprechen. Es ist zu beobachten, dass die Leistung des Endkontrollpunkts im Durchschnitt etwa 8 % unter dem hochgerechneten Wert liegt. Es wird erwartet, dass der verlustminimierende (optimale) Prüfpunkt aufgrund der unvollständigen Lernratenkühlung niedriger ist als die Extrapolationsmethode, seine Leistung ist jedoch nur etwa 4 % geringer als die der Extrapolationsmethode.
Ein ähnliches Phänomen der Leistungssättigung wurde auch in dem Datensatz beobachtet, der für die Bewertung des Sprachmodell-Bewertungstools (LM Evaluation Harness) verwendet wurde, wie in Tabelle 1 dargestellt.
Leistungssättigung ist Rangsättigung
Skalenanisotropie
Anisotropie ist eine häufige Form der Darstellungsverschlechterung, die in verschiedenen kleinen Sprachmodellen beobachtet wird. Sie beinhaltet eine Verringerung der Winkelvariabilität der Darstellungsverteilung in einem bestimmten Schicht. Frühere Untersuchungen (Ethayarajh, 2019; Godey et al., 2024) stellten fest, dass fast alle Schichten kleiner deformierter Sprachmodelle anisotrop sind. Eine übliche Methode zur Messung der Anisotropie in einer Reihe von Vektordarstellungen H ist die durchschnittliche Kosinusähnlichkeit:
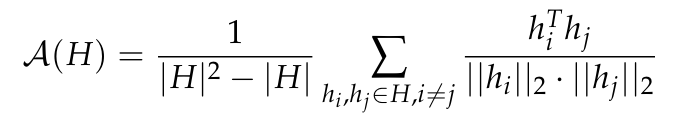
Es ist jedoch unklar, ob Anisotropie Modelle mit über einer Milliarde Parametern beeinflusst. Um dieses Problem zu lösen, berechnet dieser Artikel die durchschnittliche Kosinusähnlichkeit zwischen Schichten für eine Reihe von Modellzwischendarstellungen, nämlich GPT-2, OPT, Pythia und Gemma. In diesem Artikel wird eine Teilstichprobe von The Pile verwendet, da davon ausgegangen wird, dass die Domäne dieses Datensatzes die Domäne der in diesen Suiten verwendeten vorab trainierten Datensätze enthält oder mit dieser übereinstimmt.
In Abbildung 2 ist zu erkennen, dass die meisten Schichten der meisten Transformer-Modelle unabhängig von ihrem Maßstab bis zu einem gewissen Grad anisotrop sind. Allerdings scheint es in der letzten Schicht eine Dichotomie zu geben, wo das Modell entweder nahezu isotrop oder stark anisotrop ist. In diesem Artikel wird darauf hingewiesen, dass diese Dichotomie mit einem der Sättigungsphänomene der Pythia-Suite übereinstimmt, bei der nur Modelle mit 160 Millionen Parametern oder weniger von der Anisotropie der letzten Schicht betroffen sind.
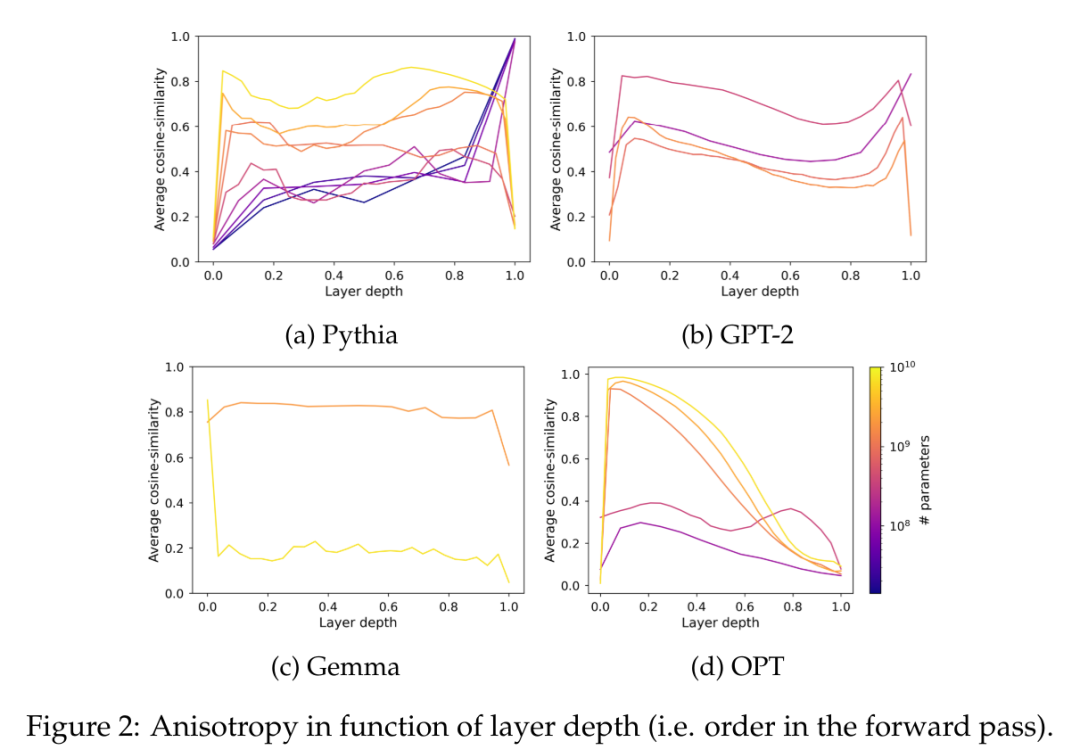
Dieser Artikel untersucht die Trainingsdynamik der Anisotropie in der Pythia-Suite und vergleicht sie mit dem Sättigungsphänomen in Abbildung 3.
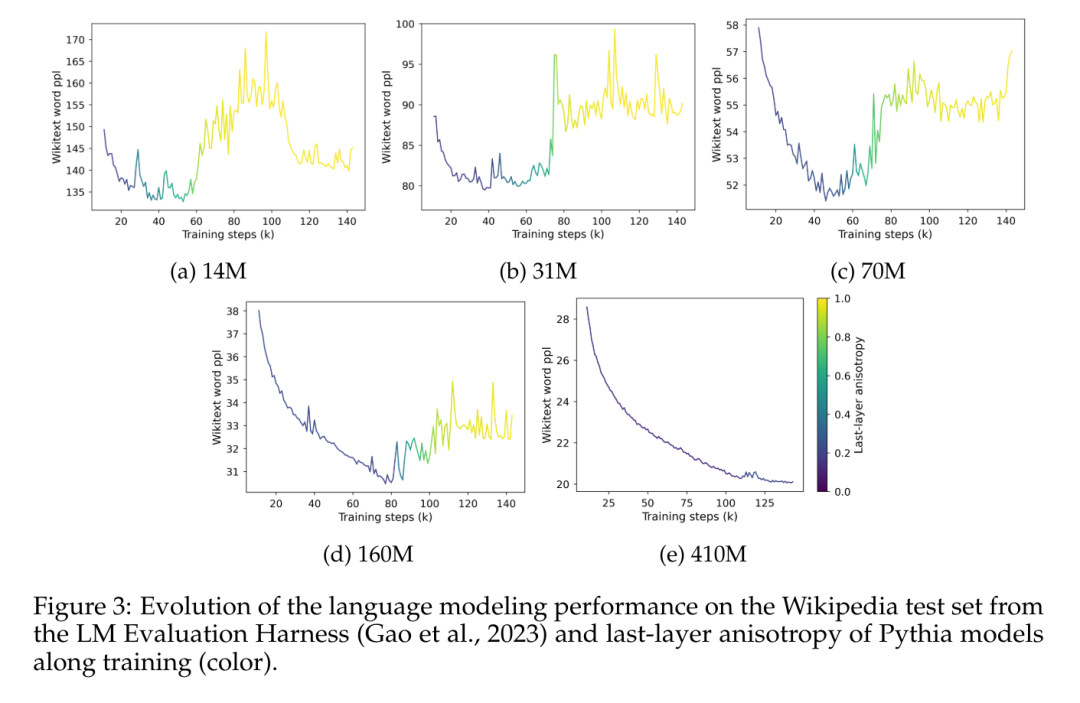
Abbildung 3 zeigt deutlich den klaren Zusammenhang zwischen dem Auftreten einer Leistungssättigung und dem Auftreten einer Anisotropie in der Darstellung der letzten Ebene des Modells. Es zeigt auch einen plötzlichen Anstieg der Anisotropie nahe dem Sättigungspunkt während des Trainings. Hier ist zu beobachten, dass das Modell innerhalb eines bestimmten domäneninternen Korpus bei Sättigung schnell an Leistung verliert und sich scheinbar nie vollständig von dieser Explosion erholt.
Singulärwertsättigung
Die mittlere Kosinusähnlichkeit ist ein wertvolles Maß für die Gleichmäßigkeit der Verteilung, aber die Einbeziehung anderer Metriken kann dazu beitragen, die Komplexität bestimmter Mannigfaltigkeiten besser zu erfassen. Darüber hinaus konzentriert es sich nur auf die Ausgabeeinbettungen des Sprachmodells und nicht auf deren Gewichte. In diesem Abschnitt wird die Analyse dieser Arbeit erweitert, indem die singuläre Werteverteilung von Sprachmodellierungsköpfen untersucht wird, um die empirischen Beobachtungen mit den theoretischen Erkenntnissen dieser Arbeit zu verbinden.
Abbildung 4 zeigt die Singulärwertverteilung entlang des endgültigen Vorhersageschichtgewichts W während des Trainings:
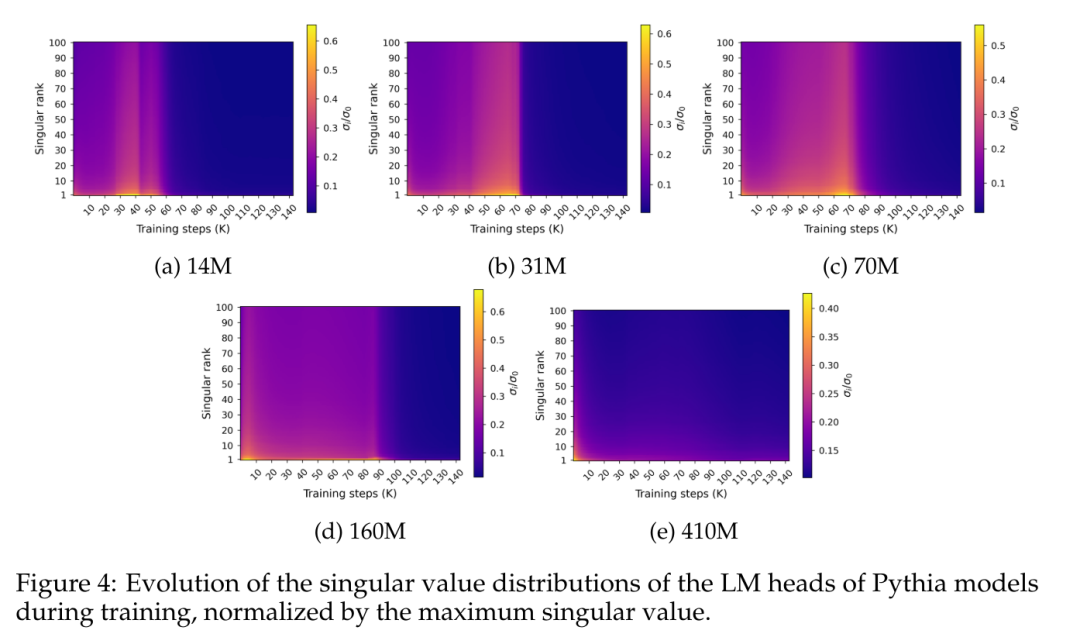
Abbildung 4 zeigt ein spezifisches Muster der spektralen Sättigung, das ungefähr gleichzeitig mit der Leistungssättigung auftritt. Die Abbildung zeigt, dass die Singulärwertverteilung während des Trainingsprozesses allmählich flacher wird, fast eine Gleichmäßigkeit erreicht, und sich dann plötzlich zu einer Spitzenverteilung entwickelt, bei der der größte Singulärwert im Vergleich zu anderen Verteilungen relativ hoch ist.
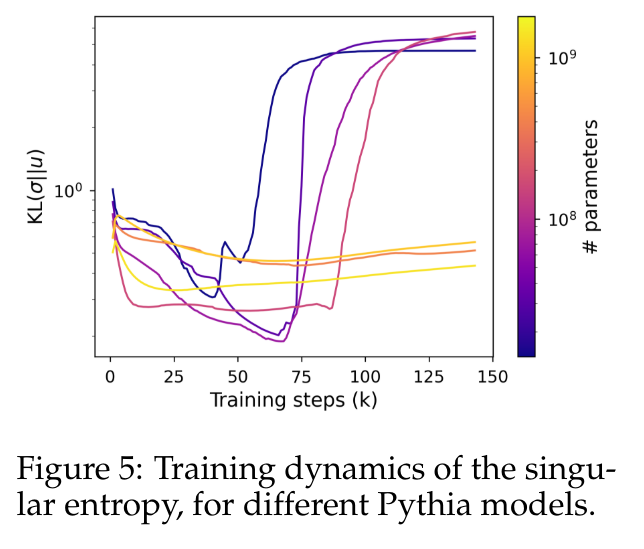
Um dieses Verhalten genauer zu quantifizieren, verwendet dieser Artikel die singuläre Entropiemetrik, die als Kullback-Leibler-Divergenz zwischen der normalisierten singulären Werteverteilung und der gleichmäßigen Verteilung berechnet wird.
Abbildung 5 zeigt, wie sich die Singulärverteilung bei einem Modell mit weniger als 410 Millionen Parametern anders entwickelt als bei einem Modell mit größeren Parametern. Die Köpfe kleiner Modelle erleben, wie ihre singulären Werteverteilungen allmählich gleichmäßiger werden, bis sie sich plötzlich verschlechtern, was wiederum mit einer verminderten Leistung des Sprachmodells korreliert. Die Singulärwertverteilung größerer Modelle ist tendenziell stabiler und zeigt während des Trainings kein offensichtliches monotones Muster.
Softmax-Engpass und Sprachdimension
Intrinsische Dimension der natürlichen Sprache
Intuitiv gesehen gilt das oben beobachtete Phänomen der Singularwertverteilungssättigung nur für kleinere Modelle, was ein Problem für den LM-Kopf darstellt. Die Abmessungen Die an der Optimierung beteiligten Personen wurden befragt. In diesem Abschnitt wird vorgeschlagen, den kritischen Wert des Rangs eines LM-Kopfes empirisch zu messen und die Dimensionen der kontextuellen Wahrscheinlichkeitsverteilung abzuschätzen, mit der die Ausgabe dieses Kopfes übereinstimmen sollte.
Um die Auswirkung des linearen Kopfrangs empirisch zu messen, schlägt dieser Artikel vor, einen rangbeschränkten Kopf auf vorab trainierten kontextuellen Darstellungen zu trainieren, die aus hochparametrisierten Sprachmodellen abgeleitet sind. Um den maximalen Rang r zu steuern, betrachten Sie einen Kopf der Form W = AB ∈ R^(V×d), wobei die Koeffizienten von A ∈ R^(V×r) und B ∈ R^(r×d) beginnen N(0,1) extrahiert (d ist die verborgene Dimension des Modells). Der Rang dieser W-Matrix wird über einen Wertebereich gescannt, der durch den Parameter r ∈ [1, d] eingeschränkt ist.
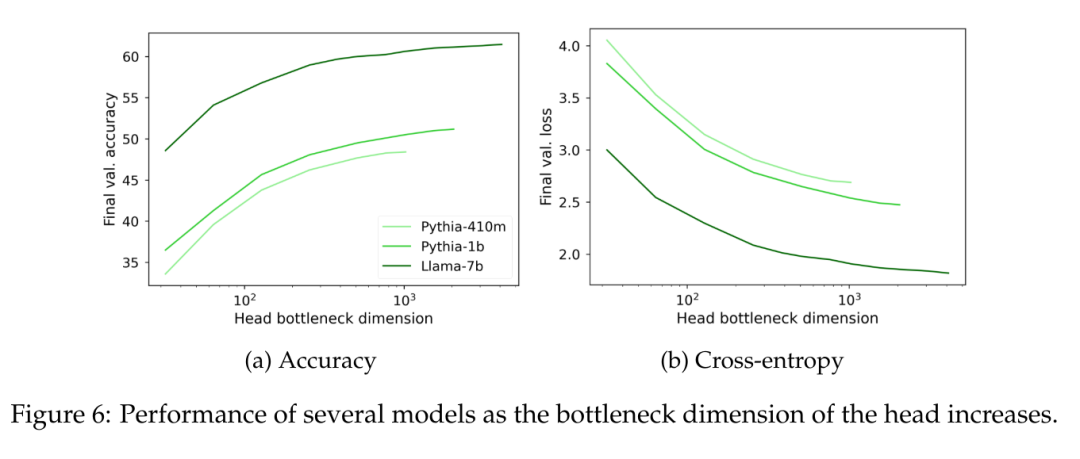
Durch Einfrieren des Sprachmodells und Trainieren des rangbeschränkten Kopfes auf etwa 150 Millionen Token, während die Lernrate an die Anzahl der trainierbaren Parameter angepasst wird.
In Abbildung 6 ist zu sehen, dass die Verwirrung unabhängig von der Modellgröße deutlich abnimmt, wenn der Rang des Sprachmodellierungsleiters W unter 1000 fällt. Dies bedeutet, dass der Kopf bei Modellen mit größeren versteckten Abmessungen keinen großen Leistungsengpass darstellt, bei Modellen mit kleineren versteckten Abmessungen kann er jedoch unabhängig von der Qualität der Ausgabedarstellung die Leistung beeinträchtigen.
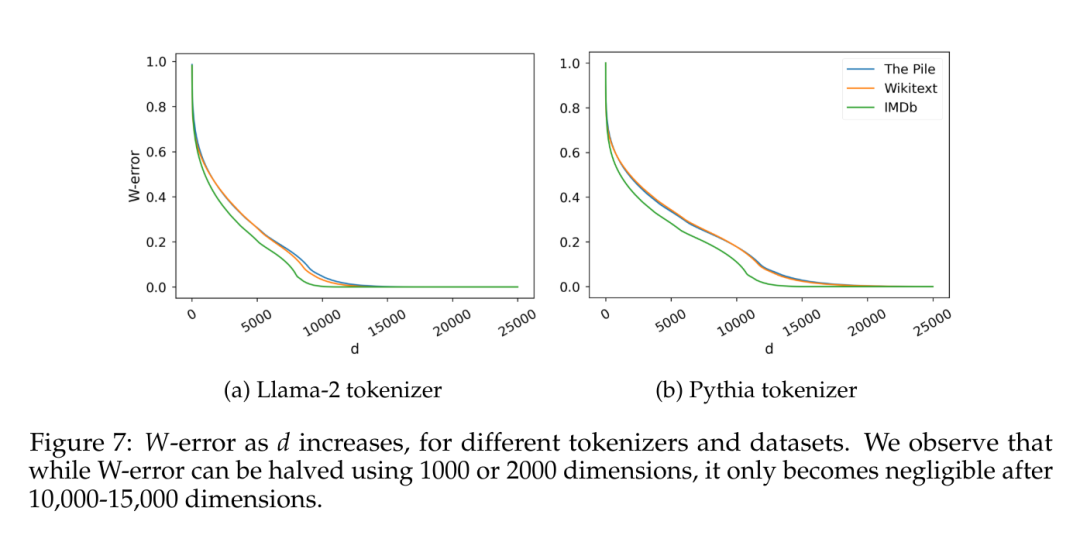
Ein weiterer interessanter Faktor ist die inhärente Dimensionalität der geschätzten Daten selbst. Um mögliche Auswirkungen im Zusammenhang mit einer spezifischen induktiven Verzerrung zu vermeiden, wurde in diesem Artikel ein naives 5-Gramm-Sprachmodell auf mehreren Datensätzen mit unterschiedlicher Abdeckung (IMDb, Wikitext und The Pile) trainiert, wobei zwei verschiedene Vokabulargrößen (30.000 Token für) verwendet wurden Lama-2, 50.000 Token für Pythia). Angesichts der beobachteten C-Werte von 5 Gramm betrachtet dieser Artikel die Matrix W ∈ R^(C×V), wobei jede Zeile die Wahrscheinlichkeitsverteilung möglicher Token bei 4 Token darstellt, und berechnet deren singuläre Wertverteilungen, wie z. B. Terashima (2003).
Abbildung 7 zeigt den W-Fehler, den minimalen Approximationsfehler für eine Matrix W mit Rang d, der durch das Eckart-Young-Mirsky-Theorem (siehe Lemma 5.2) vorhergesagt und auf die Frobenius-Norm von W normiert wurde.
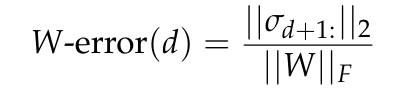
Theoretischer Engpass
Gleichzeitig kann der geschätzte Rang von W im Vergleich zur herkömmlichen Größenordnung der verborgenen Dimensionen nicht ignoriert werden. Hier analysieren wir den Zusammenhang zwischen den Abmessungen und der Leistung eines idealen Kopfes zur linearen Sprachmodellierung aus theoretischer Sicht.
Dieser Abschnitt zielt darauf ab, einen formalen Zusammenhang zwischen den inhärenten Dimensionen von Kontextverteilungen und Leistungsengpässen zu identifizieren, die auf die geringere Dimensionalität der Ausgabedarstellungen von Sprachmodellen zurückzuführen sind. Zu diesem Zweck wird ein Sprachmodellierungskopf konzipiert, der für eine ideale Kontextdarstellung optimiert ist, und die Beziehung zwischen seinen spektralen Eigenschaften und der Leistungslücke untersucht, die entsteht, wenn ein Kopf mit niedrigem Rang auf derselben Darstellung trainiert wird.
Weitere Forschungsdetails finden Sie im Originalpapier.
Das obige ist der detaillierte Inhalt vonDie Leistung kleiner Modelle ist gesättigt und die Leistung ist schlecht. Die Hauptursache ist Softmax?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
