 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Harter Kern, um Soras Physikfehler zu lösen! Vier Top-Universitäten in den Vereinigten Staaten haben gemeinsam veröffentlicht: Installieren Sie eine Physik-Engine für den Videogenerator
Harter Kern, um Soras Physikfehler zu lösen! Vier Top-Universitäten in den Vereinigten Staaten haben gemeinsam veröffentlicht: Installieren Sie eine Physik-Engine für den Videogenerator
Harter Kern, um Soras Physikfehler zu lösen! Vier Top-Universitäten in den Vereinigten Staaten haben gemeinsam veröffentlicht: Installieren Sie eine Physik-Engine für den Videogenerator
Nachdem Sora freigelassen wurde, entdeckten Benutzer einige Probleme. Obwohl das Modell die physische Welt nicht vollständig verstand, kreuzten sich die beiden Vorderbeine, was dazu führte, dass sich die Menschen unwohl fühlten Spiel erscheint unerwartet.
Die Interaktion von Objekten ist für die Erzeugung von Videorealismus sehr wichtig, aber derzeit ist es immer noch sehr schwierig, das dynamische Verhalten realer 3D-Objekte in der Interaktion zu synthetisieren.
Action Conditioned Dynamics ist ein Forschungsgebiet, das die Wahrnehmung der physikalischen Materialeigenschaften von Objekten und die 3D-Bewegungsvorhersage basierend auf diesen Eigenschaften (z. B. Objektsteifigkeit) erfordert.
Die Bewertung physikalischer Materialeigenschaften bleibt ein heikles und ungelöstes Problem, da die Messung physikalischer Materialeigenschaften realer Objekte aufgrund mangelnder Datenunterstützung äußerst schwierig ist.
Kürzlich haben das MIT, die Stanford University, die Columbia University und die Cornell University gemeinsam ein physikbasiertes Modell namens PhysDreamer vorgeschlagen, das durch Videogenerierungsmodelle gelernte Objektdynamik-Lernvorgänge nutzt, um statischen 3D-Objekten dynamisches Lernen zu ermöglichen. ??? ermöglicht es realen Objekten, auf neuartige Interaktionen wie externe Kräfte oder Agentenmanipulationen zu reagieren. Mithilfe von Benutzerstudien wurde der Realismus der synthetisierten Interaktionen bewertet, indem die Wirksamkeit des Ansatzes an verschiedenen Beispielen elastischer Objekte demonstriert wurde.
Problemformalisierung
Gegeben sei ein statisches Objekt, das durch einen 3D-Gaußschen
dargestellt wird (wobei xp die Position darstellt, αp die Opazität darstellt, Σp die Kovarianzmatrix darstellt und cp die Farbe des Partikels darstellt), das Finale Ziel ist es, Felder physikalischer Materialeigenschaften von Objekten abzuschätzen, um eine realistische interaktive Bewegungssynthese zu ermöglichen.Zu den spezifischen Eigenschaften gehören die Masse m, der Elastizitätsmodul E und das Poisson-Verhältnis ν. Der Elastizitätsmodul wird verwendet, um die Steifigkeit des Materials zu messen und die Bewegungsbahn des Objekts als Reaktion auf äußere Kräfte zu bestimmen: Ein höherer Elastizitätsmodul führt dazu um kleinere Verformungen, mehr Steifigkeit und Bewegungen mit höherer Frequenz zu erreichen.
Führen Sie eine simulierte Bewegung unter derselben Kraft, aber mit unterschiedlichem Young-Modul aus. 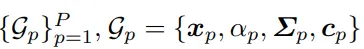 Also formalisierten die Forscher das Problem wie folgt: Durch Schätzen des räumlich variierenden Young-Modulfelds E(x) können Sie
Also formalisierten die Forscher das Problem wie folgt: Durch Schätzen des räumlich variierenden Young-Modulfelds E(x) können Sie
verwenden Fragen Sie den Elastizitätsmodul des Partikels für die Partikelsimulation ab.
Was andere physikalische Eigenschaften betrifft, kann die Masse m_p des Partikels als Produkt aus der konstanten Dichte (ρ) und dem Partikelvolumen Vp berechnet werden; das Partikelvolumen kann durch Division des „Volumens“ berechnet werden Hintergrundeinheit“ durch „Anzahl der in der Einheit enthaltenen Teilchen“ zu schätzen; der Einfluss des Poisson-Verhältnisses νp auf die Bewegung des Objekts ist vernachlässigbar und kann als konstant angenommen werden. 
Modellarchitektur
PhysDreamer kann das Materialfeld eines statischen 3D-Objekts schätzen. Die Schlüsselidee besteht darin, ein glaubwürdiges Video des sich bewegenden Objekts zu erstellen und dann das Materialfeld E(x) so zu optimieren, dass es der synthetischen Bewegung entspricht.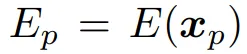 Angenommen, ein als 3D-Gaußsches Objekt dargestelltes Objekt rendern Sie es zunächst aus einem bestimmten Blickwinkel (mit Hintergrund), verwenden Sie dann ein Bild-zu-Video-Generierungsmodell, um ein Referenzvideo des Objekts in Bewegung zu generieren, und verwenden Sie dann ein differenzierbares Objekt Materialpunktmethode (MPM (Material Point Methods)) und differenzierbares Rendering, das das räumlich variierende Materialfeld und das Anfangsgeschwindigkeitsfeld optimiert, mit dem Ziel, den Unterschied zwischen dem gerenderten Video und dem Referenzvideo zu minimieren.
Angenommen, ein als 3D-Gaußsches Objekt dargestelltes Objekt rendern Sie es zunächst aus einem bestimmten Blickwinkel (mit Hintergrund), verwenden Sie dann ein Bild-zu-Video-Generierungsmodell, um ein Referenzvideo des Objekts in Bewegung zu generieren, und verwenden Sie dann ein differenzierbares Objekt Materialpunktmethode (MPM (Material Point Methods)) und differenzierbares Rendering, das das räumlich variierende Materialfeld und das Anfangsgeschwindigkeitsfeld optimiert, mit dem Ziel, den Unterschied zwischen dem gerenderten Video und dem Referenzvideo zu minimieren.
Der gepunktete Pfeil stellt den Verlaufsfluss dar
1 Grundwissen
3D-Gaußian verwendet eine Reihe anisotroper 3D-Gaußian-Kernel, um das Strahlungsfeld der 3D-Szene darzustellen. Obwohl es hauptsächlich als neue 3D-Ansichtssynthesemethode eingeführt wird, kann es direkt angewendet werden, da 3D-Gaußian über Lagrange-Eigenschaften verfügt Partikel. Ähnlich wie bei der PhysGaussian-Methode verwenden Forscher Materialpunktmethoden (MPM, Material Point Methods), um die Objektdynamik auf Gaußschen Teilchen direkt zu simulieren. Da sich die 3D-Gauß-Verteilung hauptsächlich auf der Oberfläche des Objekts befindet, kann ein optionaler interner Füllprozess angewendet werden, um den Realismus der Simulation zu verbessern. Kontinuumsmechanik und elastische Materialien In der Kontinuumsmechanik wird die Verformung des Materials durch eine Abbildungsfunktion ϕ simuliert, die den Raum des Materials im unverformten Zustand abbilden kann. Punkt Die Jacobi-Matrix F von Die Abbildungsfunktion ϕ, also der Verformungsgradient, ist der Schlüssel zum Verständnis und zur Beschreibung der Materialspannungs-Dehnungs-Beziehung, die den lokalen Verformungszustand des Materials betrifft. In hochelastischen Materialien basiert die Berechnung der Cauchy-Spannung (Spannung) auf der Dehnungsenergiedichtefunktion ψ(F), die den Grad der nicht starren Verformung des Materials quantifizieren kann. Im Allgemeinen wird diese Funktion bestimmt von Materialwissenschaftlern basierend auf dem Material, das auf der Grundlage der Prinzipien der Symmetrie und Rotationsinvarianz entworfen und mit experimentellen Daten abgeglichen wurde.
Material Point Method (MPM) Forscher verwenden die Moving Least Squares Material Point Method (MLS-MPM), um die maßgeblichen Gleichungen der „elastischen Materialdynamik“ zu lösen, wobei ρ repräsentiert die Dichte, v(x, t) repräsentiert das Geschwindigkeitsfeld des Weltraums und f repräsentiert die äußere Kraft. MPM ist eine Berechnungsmethode zur Simulation der Dynamik verschiedener Materialien. Sie kombiniert die Vorteile der Euler- und Lagrange-Methode und eignet sich besonders zur Simulation des dynamischen Verhaltens von Feststoffen, Flüssigkeiten, Sand, Stoffen. ist in der Lage, topologische Änderungen in Materialien effektiv zu bewältigen und lässt sich problemlos auf Grafikprozessoren (GPUs) parallelisieren. Die räumliche Diskretisierung erfolgt durch die Behandlung des Objekts als eine Reihe von Gaußschen Teilchen. Jedes Teilchen p stellt einen kleinen Teil des Volumens des Objekts dar und trägt Attribute wie Volumen, Masse, Position, Geschwindigkeit, Verformungsgradient und lokale Geschwindigkeit Feldgradient. In der P2G-Stufe wird der Impuls von den Partikeln auf das Gitter übertragen und das Netzwerk aktualisiert Die Geschwindigkeit auf dem Gitter wird dann an das Partikel zurückgegeben, um dessen Position und Geschwindigkeit zu aktualisieren. Gleichzeitig werden auch der lokale Geschwindigkeitsgradient und der Verformungsgradient des Partikels entsprechend aktualisiert, um den aktuellen Zustand des Materials widerzuspiegeln. MPM-Methode kann das komplexe dynamische Verhalten von Materialien, einschließlich Materialverformung, Bruch und Wechselwirkung, genau simulieren.
2. Abschätzen physikalischer Eigenschaften
Die Forscher verwendeten die Moving Least Squares Material Point Method (MLS-MPM) als physikalischen Simulator und ein hyperelastisches Materialmodell mit fester Rotation, um den Prozess dreidimensionaler Objekte zu simulieren. MLS-MPM-Simulationsprozess Der Simulator verwendet MLS-MPM, um das physikalische Verhalten des Objekts zu simulieren. Die Simulationsfunktion empfängt die Partikelposition x, die Geschwindigkeit v, den Verformungsgradienten F und das lokale Geschwindigkeitsfeld von der aktuelle Zeitschritt t. Der Gradient C sowie der physikalische Eigenschaftssatz θ des Teilchens (einschließlich der Masse, des Elastizitätsmoduls, der Poisson-Zahl und des Volumens aller Teilchen) und der Zeitschritt Δt (1×10^-4) werden genommen als Eingabe und der nächste Zeitschritt wird ausgegeben Der entsprechende Wert von t+1. Um die Dynamik zwischen benachbarten Videobildern zu simulieren, ist es normalerweise notwendig, Hunderte von Teilschritten zu iterieren. Simulation und Rendering Nach der Simulation wird die differenzierbare Rendering-Funktion Frender verwendet, um Gaußsche Partikel für jeden Frame zu rendern, wobei Rt die Rotationsmatrix aller Partikel darstellt, die aus dem Simulationsschritt erhalten wurden. Dann wird das generierte Video als Referenz verwendet, um den räumlich variierenden Young-Modul E und die Anfangsgeschwindigkeit v0 durch eine Verlustfunktion pro Bild zu optimieren, wobei die Verlustfunktion L1-Verlust und D-SSIM-Verlust und Gewicht kombiniert Der Parameter λ ist auf 0,1 eingestellt Glätte, Totalvariation-Regularisierung wird auf alle räumlichen Ebenen dieser beiden Felder angewendet. Optimierungsprozess Der Optimierungsprozess ist in zwei Phasen unterteilt, um die Stabilität zu verbessern und die Konvergenz zu beschleunigen: 2. In der zweiten Stufe wird die Anfangsgeschwindigkeit festgelegt und der räumlich variierende Elastizitätsmodul optimiert. Um zu verhindern, dass Farbverläufe explodieren oder verschwinden, fließt das Farbverlaufssignal nur zum vorherigen Frame. Auf diese Weise ist der Simulator in der Lage, das physikalische Verhalten des Objekts zu simulieren und die Materialeigenschaften und Ausgangsbedingungen auf Basis des Referenzvideos zu optimieren, um realistische dynamische Effekte zu erzeugen. 3. Beschleunigen Sie Simulationen mit Unterabtastung Die Verwendung dreidimensionaler Gaußscher Partikel für die Wiedergabe mit hoher Wiedergabetreue erfordert normalerweise Millionen von Partikeln, um eine Szene darzustellen, was einen enormen Rechenaufwand für die Ausführung von Simulationen mit sich bringt. Um die Effizienz zu verbessern, führt das Modell einen Unterabtastungsprozess ein, der den Rechenaufwand erheblich reduziert und gleichzeitig die hohe Genauigkeit der Rendering-Ergebnisse beibehält: Für die Simulation und anschließende Interpolation werden nur wenige Antriebspartikel verwendet Das Ansteuern von Partikeln, um die Position und Rotation von Gaußschen Partikeln zu ermitteln, sorgt für ein effektives Gleichgewicht zwischen Recheneffizienz und Rendering-Qualität. Konkret verwendet das Modell den K-Means-Clustering-Algorithmus, um zum Zeitpunkt t=0 einen Satz treibender Partikel zu erstellen, wobei jedes treibende Partikel durch einen Satz physikalischer Attribute dargestellt wird, einschließlich Position, Geschwindigkeit, Verformungsgradient usw lokales Geschwindigkeitsfeld. Gradient, Elastizitätsmodul, Masse, Poissonzahl und Volumen. Die Anfangsposition des treibenden Teilchens ist der Durchschnitt der Positionen aller seiner Clustermitglieder, wobei die Anzahl der treibenden Teilchen viel kleiner ist als die Anzahl der dreidimensionalen Gaußschen Teilchen. Während des Rendervorgangs werden die Position und Drehung jedes dreidimensionalen Gaußschen Teilchens durch Interpolation der Position und Drehung des Antriebsteilchens berechnet: Finden Sie für jedes dreidimensionale Gaußsche Teilchen zunächst die acht nächsten benachbarten Antriebsteilchen zum Zeitpunkt t =0, Die Starrkörpertransformation T zwischen diesen acht Antriebspartikeln bei t=0 und dem aktuellen Zeitstempel wird dann angepasst, um die aktuelle Position und Rotation der Partikel zu bestimmen. Experimentelle Ergebnisse (eine rote Rose, eine Nelke, eine orangefarbene Rose, eine Tulpe und eine weiße Rose), eine Alocasia, ein Telefonkabel und eine Mütze. Nehmen Sie dann vier interaktive Videos auf, um ihre natürliche Bewegung nach der Interaktion zu beschreiben, z. B. Stochern oder Ziehen , und verwenden Sie echtes Video als zusätzliche Referenz zum Vergleich. Experimentelle Ergebnisse Qualitative Analyseergebnisse zum räumlich variierenden Young-Modul (eine physikalische Größe, die die Elastizität eines Materials misst) In Benutzerstudien, verglichen mit Basismethoden und echten Nachher Ein Vergleich der weltweit aufgenommenen Videos zeigt, dass mehr als 80 % der Teilnehmer das PhysDreamer-Modell im Two-Choice-Experiment (2AFC) bevorzugten, da sie der Meinung waren, dass es hinsichtlich der Authentizität der Bewegung in Bezug auf die visuelle Qualität überlegen sei. Außerdem bevorzugen 65 % der Teilnehmer PhysDreamerDa die verglichenen statischen Szenen selbst konsistent sind, ist die Bewertung der visuellen Qualität in gewissem Maße auch auf dem Bewegungseffekt der generierten Objekte angewiesen. Aus den Schnitten der Bewegungsmuster zu verschiedenen Zeitpunkten lässt sich erkennen, dass PhysGaussian eine prinzipielle Schätzung der Materialeigenschaften fehlt, was dazu führt, dass die von ihm erzeugte Bewegungsamplitude zu groß und zu langsam ist, was nicht mit der Realität übereinstimmt . Im Vergleich zu DreamGaussian4D bevorzugen 70 % und 63,5 % der 2AFC-Proben das PhysDreamer-Modell in Bezug auf visuelle Qualität und Bewegungsauthentizität. Wie aus dem Bild oben ersichtlich ist, ist die von DreamGaussian4D erzeugte Bewegung periodisch und die Amplitude wird auf einem kleinen konstanten Wert gehalten. Im Gegensatz dazu kann PhysDreamer den Dämpfungseffekt in Bewegung simulieren. 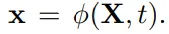
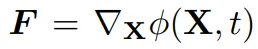
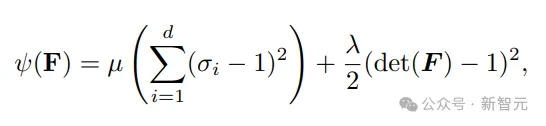
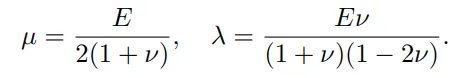
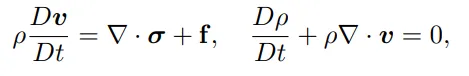
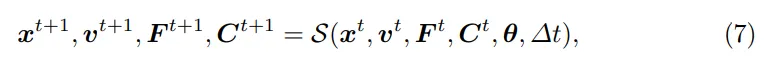
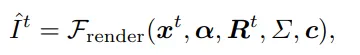
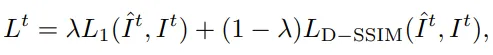
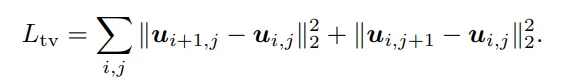 1. In der ersten Phase beträgt der Yang-Modul jedes Gaußschen Teilchens zufällig initialisiert und fixiert, und dann werden nur die ersten drei Bilder des Referenzvideos verwendet, um die Anfangsgeschwindigkeit jedes Partikels zu optimieren.
1. In der ersten Phase beträgt der Yang-Modul jedes Gaußschen Teilchens zufällig initialisiert und fixiert, und dann werden nur die ersten drei Bilder des Referenzvideos verwendet, um die Anfangsgeschwindigkeit jedes Partikels zu optimieren. 
Das obige ist der detaillierte Inhalt vonHarter Kern, um Soras Physikfehler zu lösen! Vier Top-Universitäten in den Vereinigten Staaten haben gemeinsam veröffentlicht: Installieren Sie eine Physik-Engine für den Videogenerator. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Welche Bibliotheken werden für die Operationen der schwimmenden Punktzahl in Go verwendet?
Apr 02, 2025 pm 02:06 PM
Welche Bibliotheken werden für die Operationen der schwimmenden Punktzahl in Go verwendet?
Apr 02, 2025 pm 02:06 PM
In der Bibliothek, die für den Betrieb der Schwimmpunktnummer in der GO-Sprache verwendet wird, wird die Genauigkeit sichergestellt, wie die Genauigkeit ...
 So führen Sie das H5 -Projekt aus
Apr 06, 2025 pm 12:21 PM
So führen Sie das H5 -Projekt aus
Apr 06, 2025 pm 12:21 PM
Ausführen des H5 -Projekts erfordert die folgenden Schritte: Installation der erforderlichen Tools wie Webserver, Node.js, Entwicklungstools usw. Erstellen Sie eine Entwicklungsumgebung, erstellen Sie Projektordner, initialisieren Sie Projekte und schreiben Sie Code. Starten Sie den Entwicklungsserver und führen Sie den Befehl mit der Befehlszeile aus. Vorschau des Projekts in Ihrem Browser und geben Sie die Entwicklungsserver -URL ein. Veröffentlichen Sie Projekte, optimieren Sie Code, stellen Sie Projekte bereit und richten Sie die Webserverkonfiguration ein.
 Gitee Pages statische Website -Bereitstellung fehlgeschlagen: Wie können Sie einzelne Dateien 404 Fehler beheben und beheben?
Apr 04, 2025 pm 11:54 PM
Gitee Pages statische Website -Bereitstellung fehlgeschlagen: Wie können Sie einzelne Dateien 404 Fehler beheben und beheben?
Apr 04, 2025 pm 11:54 PM
GitePages statische Website -Bereitstellung fehlgeschlagen: 404 Fehlerbehebung und Auflösung bei der Verwendung von Gitee ...
 Welche Bibliotheken in GO werden von großen Unternehmen entwickelt oder von bekannten Open-Source-Projekten bereitgestellt?
Apr 02, 2025 pm 04:12 PM
Welche Bibliotheken in GO werden von großen Unternehmen entwickelt oder von bekannten Open-Source-Projekten bereitgestellt?
Apr 02, 2025 pm 04:12 PM
Welche Bibliotheken in GO werden von großen Unternehmen oder bekannten Open-Source-Projekten entwickelt? Bei der Programmierung in Go begegnen Entwickler häufig auf einige häufige Bedürfnisse, ...
 Wie gibt ich die mit dem Modell in Beego Orm zugeordnete Datenbank an?
Apr 02, 2025 pm 03:54 PM
Wie gibt ich die mit dem Modell in Beego Orm zugeordnete Datenbank an?
Apr 02, 2025 pm 03:54 PM
Wie kann man im Beegoorm -Framework die mit dem Modell zugeordnete Datenbank angeben? In vielen BeEGO -Projekten müssen mehrere Datenbanken gleichzeitig betrieben werden. Bei Verwendung von BeEGO ...
 Bedarf die Produktion von H5 -Seiten eine kontinuierliche Wartung?
Apr 05, 2025 pm 11:27 PM
Bedarf die Produktion von H5 -Seiten eine kontinuierliche Wartung?
Apr 05, 2025 pm 11:27 PM
Die H5 -Seite muss aufgrund von Faktoren wie Code -Schwachstellen, Browserkompatibilität, Leistungsoptimierung, Sicherheitsaktualisierungen und Verbesserungen der Benutzererfahrung kontinuierlich aufrechterhalten werden. Zu den effektiven Wartungsmethoden gehören das Erstellen eines vollständigen Testsystems, die Verwendung von Versionstools für Versionskontrolle, die regelmäßige Überwachung der Seitenleistung, das Sammeln von Benutzern und die Formulierung von Wartungsplänen.
 Wie löste ich das Problem des Typs des user_id -Typs bei der Verwendung von Redis -Stream, um Nachrichtenwarteschlangen in GO -Sprache zu implementieren?
Apr 02, 2025 pm 04:54 PM
Wie löste ich das Problem des Typs des user_id -Typs bei der Verwendung von Redis -Stream, um Nachrichtenwarteschlangen in GO -Sprache zu implementieren?
Apr 02, 2025 pm 04:54 PM
Das Problem der Verwendung von RETISTREAM zur Implementierung von Nachrichtenwarteschlangen in der GO -Sprache besteht darin, die Go -Sprache und Redis zu verwenden ...
 Python Hourglass Graph Drawing: Wie vermeiden Sie variable undefinierte Fehler?
Apr 01, 2025 pm 06:27 PM
Python Hourglass Graph Drawing: Wie vermeiden Sie variable undefinierte Fehler?
Apr 01, 2025 pm 06:27 PM
Erste Schritte mit Python: Hourglas -Grafikzeichnung und Eingabeüberprüfung In diesem Artikel wird das Problem der Variablendefinition gelöst, das von einem Python -Anfänger im Hourglass -Grafikzeichnungsprogramm auftritt. Code...



