Quantilregression für probabilistische Zeitreihenprognosen

Ändern Sie nicht die Bedeutung des ursprünglichen Inhalts, optimieren Sie den Inhalt nicht, schreiben Sie den Inhalt neu und schreiben Sie nicht weiter. „Die Quantilregression erfüllt diesen Bedarf, indem sie Vorhersageintervalle mit quantifizierten Chancen bereitstellt. Dabei handelt es sich um eine statistische Technik zur Modellierung der Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen, insbesondere wenn die bedingte Verteilung der Antwortvariablen von Interesse ist. Im Gegensatz zur herkömmlichen Regression Methoden: Die Quantilregression konzentriert sich auf die Schätzung der bedingten Größe der Antwortvariablen und nicht auf den bedingten Mittelwert lineare Beziehung zwischen einer Menge von Regressoren X und den Quantilen der erklärten Variablen Y.

Das bestehende Regressionsmodell ist eigentlich eine Methode zur Untersuchung der Beziehung zwischen der erklärten Variablen und der erklärenden Variablen. Sie konzentrieren sich auf die Beziehung zwischen den erklärenden Variablen und den erklärten Variablen sowie deren Fehlerverteilung. Medianregression und Quantilregression sind zwei gängige Regressionsmodelle. Sie wurden erstmals von Koenker und Bassett (1978) vorgeschlagen. 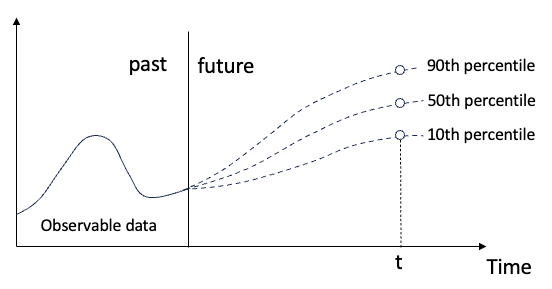Die Berechnung des gewöhnlichen Regressionsschätzers der kleinsten Quadrate basiert auf der Minimierung der Summe der quadrierten Residuen. Die Berechnung des Quantil-Regressionsschätzers basiert ebenfalls auf der Minimierung des Absolutwert-Residuums in symmetrischer Form. Unter diesen ist die Median-Regressionsoperation der kleinste absolute Abweichungsschätzer (LAD, kleinster absoluter Abweichungsschätzer).

Vorteile der Quantilregression

Erläutern Sie das vollständige Bild der bedingten Verteilung der erklärten Variablen. Sie analysiert nicht nur den bedingten Erwartungswert (Mittelwert) der erklärten Variablen, sondern analysiert auch, wie sich die erklärende Variable auf den Median und das Quantil der erklärten Variablen auswirkt erklärte Variable. Anzahl usw. Die Schätzungen der Regressionskoeffizienten bei verschiedenen Quantilen sind oft unterschiedlich, das heißt, die erklärenden Variablen haben unterschiedliche Auswirkungen auf verschiedene Quantile. Daher haben die unterschiedlichen Auswirkungen verschiedener Quantile der erklärenden Variablen unterschiedliche Auswirkungen auf die erklärten Variablen.

Im Vergleich zur Methode der kleinsten Multiplikation ist die Schätzmethode der Median-Regression robuster gegenüber Ausreißern, und die Quantil-Regression erfordert keine starken Annahmen über den Fehlerterm, sodass für nicht normale Zustände die Zustandsverteilung und der Median-Regressionskoeffizient gesünder sind. Gleichzeitig wird die Mengenschätzung des Quantilregressionssystems robuster.

Was sind die Vorteile der Quantilregression gegenüber der Monte-Carlo-Simulation? Erstens schätzt die Quantilregression direkt die bedingte Größe der Antwortvariablen angesichts der Prädiktoren. Dies bedeutet, dass sie nicht wie eine Monte-Carlo-Simulation eine große Anzahl möglicher Ergebnisse liefert, sondern eine Schätzung einer bestimmten Größenordnung der Verteilung der Antwortvariablen liefert. Dies ist besonders nützlich, um unterschiedliche Grade der Prognoseunsicherheit zu verstehen, beispielsweise Quintile, Quartile oder extreme Größenordnungen. Zweitens bietet die Quantilregression eine modellbasierte Methode zur Schätzung der Vorhersageunsicherheit, die Beobachtungsdaten verwendet, um die Beziehung zwischen Variablen abzuschätzen und auf der Grundlage dieser Beziehung Vorhersagen zu treffen. Im Gegensatz dazu beruht die Monte-Carlo-Simulation auf der Angabe von Wahrscheinlichkeitsverteilungen für Eingabevariablen und der Generierung von Ergebnissen auf der Grundlage von Zufallsstichproben.

NeuralProphet bietet zwei statistische Techniken: (1) Quantilregression und (2) konforme Quantilregression. Die konforme Quantilvorhersagetechnik fügt einen Kalibrierungsprozess hinzu, um eine Quantilregression durchzuführen. In diesem Artikel verwenden wir das Quantil-Regressionsmodul von Neural Prophet, um Quantil-Regressionsvorhersagen zu treffen. Dieses Modul fügt einen Kalibrierungsprozess hinzu, um sicherzustellen, dass die Vorhersageergebnisse mit der Verteilung der beobachteten Daten übereinstimmen. In diesem Kapitel verwenden wir das Quantilregressionsmodul von Neural Prophet.

Umweltanforderungen

Installieren Sie NeuralProphet.

!pip install neuralprophet!pip uninstall numpy!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5

Importieren Sie die erforderlichen Bibliotheken.

%matplotlib inlinefrom matplotlib import pyplot as pltimport pandas as pdimport numpy as npimport loggingimport warningslogging.getLogger('prophet').setLevel(logging.ERROR)warnings.filterwarnings("ignore")

Datensatz

Geteilte Fahrraddaten. Bei dem Datensatz handelt es sich um einen multivariaten Datensatz, der die tägliche Mietnachfrage sowie weitere Wetterfelder wie Temperatur oder Windgeschwindigkeit enthält.

data = pd.read_csv('/bike_sharing_daily.csv')data.tail()

Bild (B): Geteilte Fahrräder

Plotten Sie die Anzahl der geteilten Fahrräder. Wir beobachteten, dass die Nachfrage im zweiten Jahr anstieg und einem saisonalen Muster folgte.

# convert string to datetime64data["ds"] = pd.to_datetime(data["dteday"])# create line plot of sales dataplt.plot(data['ds'], data["cnt"])plt.xlabel("date")plt.ylabel("Count")plt.show()

Bild (C): Tägliche Nachfrage nach Fahrradverleih

Machen Sie die grundlegendste Datenvorbereitung für die Modellierung. NeuralProphet erfordert die Spaltennamen ds und y, was mit Prophet identisch ist.

df = data[['ds','cnt']]df.columns = ['ds','y']

构建分位数回归模型

直接在 NeuralProphet 中构建分位数回归。假设我们需要第 5、10、50、90 和 95 个量级的值。我们指定 quantile_list = [0.05,0.1,0.5,0.9,0.95]，并打开参数 quantiles = quantile_list。

from neuralprophet import NeuralProphet, set_log_levelquantile_list=[0.05,0.1,0.5,0.9,0.95 ]# Model and predictionm = NeuralProphet(quantiles=quantile_list,yearly_seasnotallow=True,weekly_seasnotallow=True,daily_seasnotallow=False)m = m.add_country_holidays("US")m.set_plotting_backend("matplotlib")# Use matplotlibdf_train, df_test = m.split_df(df, valid_p=0.2)metrics = m.fit(df_train, validation_df=df_test, progress="bar")metrics.tail()

分位数回归预测

我们将使用 .make_future_dataframe()为预测创建新数据帧，NeuralProphet 是基于 Prophet 的。参数 n_historic_predictions 为 100，只包含过去的 100 个数据点。如果设置为 True，则包括整个历史数据。我们设置 period=50 来预测未来 50 个数据点。

future = m.make_future_dataframe(df, periods=50, n_historic_predictinotallow=100) #, n_historic_predictinotallow=1)# Perform prediction with the trained modelsforecast = m.predict(df=future)forecast.tail(60)

预测结果存储在数据框架 predict 中。

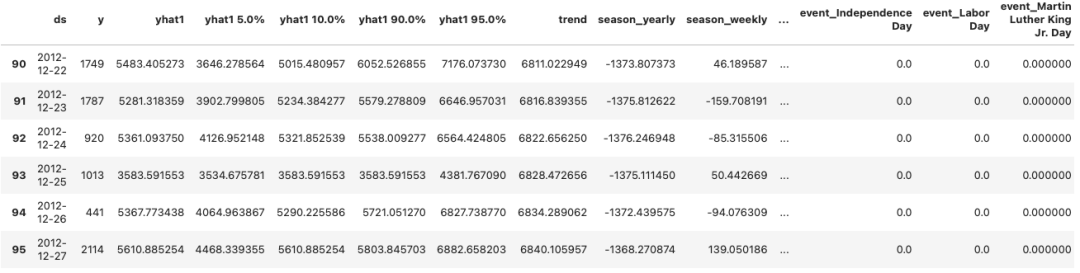图 (D)：预测

上述数据框架包含了绘制地图所需的所有数据元素。

m.plot(forecast, plotting_backend="plotly-static"#plotting_backend = "matplotlib")

预测区间是由分位数值提供的！

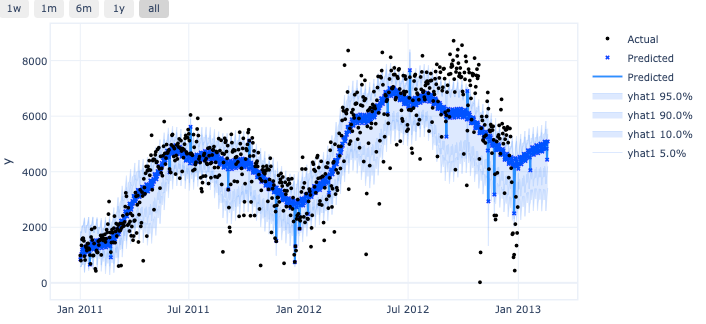图 (E)：分位数预测

预测区间和置信区间的区别

预测区间和置信区间在流行趋势中很有帮助，因为它们可以量化不确定性。它们的目标、计算方法和应用是不同的。下面我将用回归来解释两者的区别。在图(F)中，我在左边画出了线性回归，在右边画出了分位数回归。

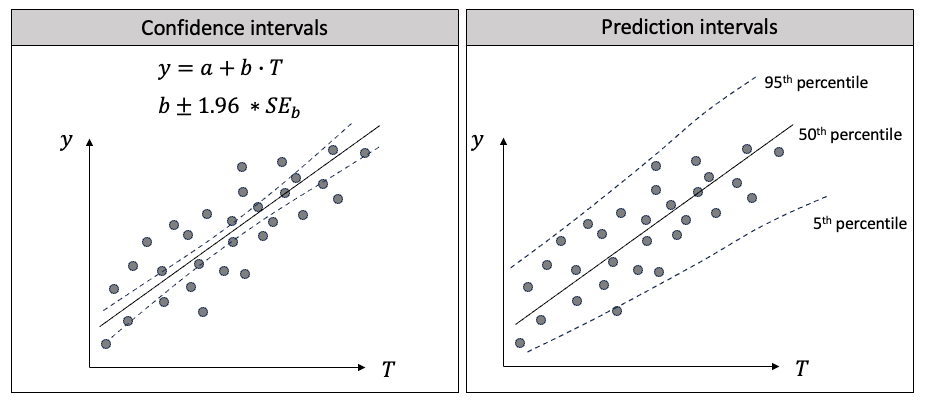图(F)：置信区间与预测区间的区别

首先，它们的目标不同：

• 线性回归的主要目标是找到一条线，使预测值尽可能接近给定自变量值时因变量的条件均值。
• 分位数回归旨在提供未来观测值的范围，在一定的置信度下。它估计自变量与因变量条件分布的不同量化值之间的关系。

其次，它们的计算方法不同：

• 在线性回归中，置信区间是对自变量系数的区间估计，通常使用普通最小二乘法 (OLS) 找出数据点到直线的最小总距离。系数的变化会影响预测的条件均值 Y。
• 在分位数回归中，你可以选择依赖变量的不同量级来估计回归系数，通常是最小化绝对偏差的加权和，而不是使用OLS方法。

第三，它们的应用不同：

• 在线性回归中，预测的条件均值有 95% 的置信区间。置信区间较窄，因为它是条件平均值，而不是整个范围。
• 在分位数回归中，预测值有 95% 的概率落在预测区间的范围内。

写在最后

本文介绍了分位数回归预测区间的概念，以及如何利用 NeuralProphet 生成预测区间。我们还强调了预测区间和置信区间之间的差异，这在商业应用中经常引起混淆。后面将继续探讨另一项重要的技术，即复合分位数回归（CQR），用于预测不确定性。

Das obige ist der detaillierte Inhalt vonQuantilregression für probabilistische Zeitreihenprognosen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!