 Web-Frontend
Web-Frontend
 js-Tutorial
js-Tutorial
 Detaillierte Erläuterung des Binärbaums von JavaScript-Datenstrukturen und -Algorithmen. Grundkenntnisse
Detaillierte Erläuterung des Binärbaums von JavaScript-Datenstrukturen und -Algorithmen. Grundkenntnisse
Detaillierte Erläuterung des Binärbaums von JavaScript-Datenstrukturen und -Algorithmen. Grundkenntnisse
Das Konzept des Binärbaums
Binärbaum ist eine endliche Menge von n (n>=0) Knoten. Die Menge ist entweder eine leere Menge (leerer Binärbaum) oder sie besteht aus einem Wurzelknoten und zwei voneinander disjunkten Bäumen bestehend aus dem linken Teilbaum und dem rechten Teilbaum des Wurzelknotens.

Eigenschaften von Binärbäumen
Jeder Knoten hat höchstens zwei Teilbäume, daher gibt es im Binärbaum keinen Knoten mit einem Grad größer als 2. Jeder Knoten im Binärbaum ist ein Objekt, und jeder Datenknoten verfügt über drei Zeiger, nämlich Zeiger auf den übergeordneten Knoten, den linken untergeordneten Knoten und den rechten untergeordneten Knoten. Jeder Knoten ist über Zeiger miteinander verbunden. Die Beziehung zwischen verbundenen Zeigern ist eine Eltern-Kind-Beziehung.
Definition des Binärbaumknotens
Binärbaumknoten sind wie folgt definiert:
struct BinaryTreeNode
{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
};
Fünf Grundformen von Binärbäumen
Leerer Binärbaum
Es gibt nur einen Wurzelknoten
Der Wurzelknoten hat nur den linken Teilbaum
Der Wurzelknoten hat nur den rechten Teilbaum
Der Wurzelknoten hat sowohl linke als auch rechte Teilbäume

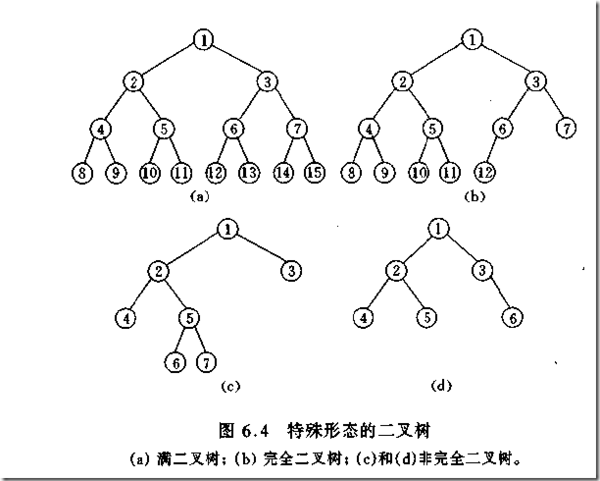
Für einen gewöhnlichen Baum mit drei Knoten gibt es nur zwei Situationen: zwei Schichten oder drei Schichten. Da der Binärbaum jedoch links und rechts unterscheiden muss, entwickelt er sich zu den folgenden fünf Formen:

Spezieller Binärbaum
Schräger Baum
Wie im 2. und 3. Bild im letzten Bild oben gezeigt.
Vollständiger Binärbaum
Wenn in einem Binärbaum alle Zweigknoten linke und rechte Teilbäume haben und sich alle Blätter auf derselben Ebene befinden, wird ein solcher Binärbaum als vollständiger Binärbaum bezeichnet. Wie unten gezeigt:
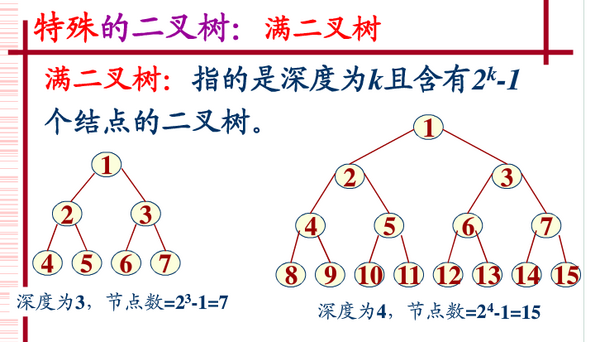
Vollständiger Binärbaum
Ein vollständiger Binärbaum bedeutet, dass die linke Seite der letzten Ebene voll ist, die rechte Seite voll sein kann oder nicht und dann die verbleibenden Ebenen voll sind. Ein Binärbaum mit der Tiefe k und der Anzahl der Knoten 2^k - 1 ist ein vollständiger Binärbaum (vollständiger Binärbaum). Es ist ein Baum mit der Tiefe k und ohne Lücken.
Die Merkmale eines vollständigen Binärbaums sind:
Blattknoten können nur auf den unteren beiden Ebenen erscheinen.
Die untersten Blätter müssen auf die linke durchgehende Position konzentriert werden.
Wenn auf der vorletzten Ebene Blattknoten vorhanden sind, müssen diese sich an kontinuierlichen Positionen auf der rechten Seite befinden.
Wenn der Knotengrad 1 ist, hat der Knoten nur noch untergeordnete Elemente.
Ein Binärbaum mit demselben Knotenbaum, ein vollständiger Binärbaum hat die geringste Tiefe.
Hinweis: Ein vollständiger Binärbaum muss ein vollständiger Binärbaum sein, aber ein vollständiger Binärbaum ist nicht unbedingt ein vollständiger Binärbaum.
Der Algorithmus ist wie folgt:
bool is_complete(tree *root)
{
Warteschlange q;
Baum *ptr;
// Breitendurchquerung (Ebenendurchquerung) durchführen und NULL-Knoten in die Warteschlange stellen
q.push(root);
While ((ptr = q.pop()) != NULL)
{
q.push(ptr->left); q.push(ptr->right); }
// Bestimmen Sie, ob es unbesuchte Knoten gibt While (!q.is_empty())
{
ptr = q.pop();
// Wenn es nicht besuchte Nicht-NULL-Knoten gibt, weist der Baum Lücken auf und ist ein unvollständiger Binärbaum
return false;
}
gibt true zurück;
}
Eigenschaften von Binärbäumen
Eigenschaft 1 eines Binärbaums: Es gibt höchstens 2^(i-1) Knoten (i>=1) auf der i-ten Ebene des Binärbaums
Eigenschaft 2 von Binärbäumen: Ein Binärbaum mit Tiefe k hat höchstens 2^k-1 Knoten (k>=1)
Sequentielle Speicherstruktur des Binärbaums
Die sequentielle Speicherstruktur eines Binärbaums verwendet ein eindimensionales Array, um jeden Knoten im Binärbaum zu speichern, und der Speicherort der Knoten kann die logische Beziehung zwischen den Knoten widerspiegeln.

Binär verknüpfte Liste
Da die Anwendbarkeit der sequentiellen Speicherung nicht stark ist, müssen wir die Kettenspeicherstruktur berücksichtigen. Nach internationaler Praxis wird bei der Speicherung von Binärbäumen im Allgemeinen eine Kettenspeicherstruktur verwendet.
Jeder Knoten eines Binärbaums hat höchstens zwei Kinder, daher ist es eine natürliche Idee, ein Datenfeld und zwei Zeigerfelder dafür zu entwerfen. Wir nennen eine solche verknüpfte Liste eine binär verknüpfte Liste.

Binäre Baumdurchquerung
Das Durchlaufen eines Binärbaums bedeutet, vom Wurzelknoten aus zu beginnen und alle Knoten im Binärbaum in einer bestimmten Reihenfolge zu besuchen, sodass jeder Knoten nur einmal besucht wird.
Es gibt drei Möglichkeiten, einen Binärbaum zu durchlaufen:
(1) Vorbestellungsdurchquerung (DLR), besuchen Sie zuerst den Wurzelknoten, durchqueren Sie dann den linken Teilbaum und durchqueren Sie schließlich den rechten Teilbaum. Die Abkürzung root-left-right.
(2) In-Order-Traversal (LDR), durchquert zuerst den linken Teilbaum, besucht dann den Wurzelknoten und durchquert schließlich den rechten Teilbaum. Abgekürzt als left-root-right.
(3) Post-Order-Traversal (LRD), durchquert zuerst den linken Teilbaum, dann den rechten Teilbaum und besucht schließlich den Wurzelknoten. Abgekürzt als Links-Rechts-Wurzel.
Durchquerung vorbestellen:
Wenn der Binärbaum leer ist, wird keine Operation zurückgegeben, andernfalls wird zuerst der Wurzelknoten besucht, dann wird der linke Teilbaum in Vorbestellung durchlaufen und dann wird der rechte Teilbaum in Vorbestellung durchlaufen.
Die Durchlaufreihenfolge ist: A B D H I E J C F K G
//Durchquerung vorbestellen
Funktion preOrder(node){
If(!node == null){
putstr(node.show() " ");
preOrder(node.left);
preOrder(node.right);
}
}
Durchlauf in der Reihenfolge:
Wenn der Baum leer ist, wird keine Operation zurückgegeben. Andernfalls durchlaufen Sie ausgehend vom Wurzelknoten (beachten Sie, dass der Wurzelknoten nicht zuerst besucht wird) den linken Teilbaum des Wurzelknotens der Reihe nach und besuchen Sie dann den Wurzelknoten. und schließlich den rechten Teilbaum der Reihe nach durchlaufen.

Die Durchlaufreihenfolge ist: H D I B E J A F K C G
//Rekursion verwenden, um die Durchquerung in der Reihenfolge zu implementieren
Funktion inOrder(node){
If(!(node == null)){
inOrder(node.left);//Besuchen Sie zuerst den linken Teilbaum
putstr(node.show() " ");//Besuchen Sie den Stammknoten erneut
inOrder(node.right);//Letzter Zugriff auf den rechten Teilbaum
}
}
Post-Order-Traversal:
Wenn der Baum leer ist, kehrt die No-Op-Operation zurück, andernfalls werden die linken und rechten Teilbäume von links nach rechts durchlaufen, zuerst die Blätter und dann die Knoten, und schließlich wird der Wurzelknoten besucht.

Die Durchlaufreihenfolge ist: H I D J E B K F G C A
//Post-Order-Traversal
Funktion postOrder(node){
If(!node == null){
PostOrder(node.left);
postOrder(node.right);
putStr(node.show() " ");
}
}
Binären Suchbaum implementieren
Der binäre Suchbaum (BST) besteht aus Knoten, daher definieren wir ein Knotenknotenobjekt wie folgt:
Funktion Node(data,left,right){
This.data = data;
This.left = left;//Speichern Sie den Link zum linken Knoten
This.right = richtig;
This.show = show;
}
Funktion show(){
Return this.data;//Anzeige der im Knoten gespeicherten Daten
}
Finden Sie die Maximal- und Minimalwerte
Das Finden der Minimal- und Maximalwerte auf einem BST ist sehr einfach, da sich der kleinere Wert immer auf dem linken untergeordneten Knoten befindet. Um den Minimalwert auf einem BST zu finden, durchlaufen Sie einfach den linken Teilbaum, bis der letzte Knoten gefunden wird
Finden Sie den Mindestwert
Funktion getMin(){
var current = this.root;
While(!(current.left == null)){
Current = current.left;
}
Gibt current.data zurück;
}
Diese Methode durchläuft nacheinander den linken Teilbaum des BST, bis sie zum Knoten ganz links des BST gelangt, der wie folgt definiert ist:
current.left = null;
Zu diesem Zeitpunkt ist der auf dem aktuellen Knoten gespeicherte Wert der Mindestwert
Finden Sie den Maximalwert
Um den Maximalwert auf BST zu finden, muss nur der rechte Teilbaum durchlaufen werden, bis der letzte Knoten gefunden wird, und der auf diesem Knoten gespeicherte Wert ist der Maximalwert.
Funktion getMax(){
var current = this.root;
While(!(current.right == null)){
current = current.right;
}
Gibt current.data zurück;
}

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Zu den häufigsten Herausforderungen, mit denen Algorithmen für maschinelles Lernen in C++ konfrontiert sind, gehören Speicherverwaltung, Multithreading, Leistungsoptimierung und Wartbarkeit. Zu den Lösungen gehören die Verwendung intelligenter Zeiger, moderner Threading-Bibliotheken, SIMD-Anweisungen und Bibliotheken von Drittanbietern sowie die Einhaltung von Codierungsstilrichtlinien und die Verwendung von Automatisierungstools. Praktische Fälle zeigen, wie man die Eigen-Bibliothek nutzt, um lineare Regressionsalgorithmen zu implementieren, den Speicher effektiv zu verwalten und leistungsstarke Matrixoperationen zu nutzen.
 Entdecken Sie die zugrunde liegenden Prinzipien und die Algorithmusauswahl der C++-Sortierfunktion
Apr 02, 2024 pm 05:36 PM
Entdecken Sie die zugrunde liegenden Prinzipien und die Algorithmusauswahl der C++-Sortierfunktion
Apr 02, 2024 pm 05:36 PM
Die unterste Ebene der C++-Sortierfunktion verwendet die Zusammenführungssortierung, ihre Komplexität beträgt O(nlogn) und bietet verschiedene Auswahlmöglichkeiten für Sortieralgorithmen, einschließlich schneller Sortierung, Heap-Sortierung und stabiler Sortierung.
 Vergleichen Sie komplexe Datenstrukturen mithilfe des Java-Funktionsvergleichs
Apr 19, 2024 pm 10:24 PM
Vergleichen Sie komplexe Datenstrukturen mithilfe des Java-Funktionsvergleichs
Apr 19, 2024 pm 10:24 PM
Bei der Verwendung komplexer Datenstrukturen in Java wird Comparator verwendet, um einen flexiblen Vergleichsmechanismus bereitzustellen. Zu den spezifischen Schritten gehören: Definieren einer Komparatorklasse und Umschreiben der Vergleichsmethode, um die Vergleichslogik zu definieren. Erstellen Sie eine Komparatorinstanz. Verwenden Sie die Methode „Collections.sort“ und übergeben Sie die Sammlungs- und Komparatorinstanzen.
 Verbesserter Erkennungsalgorithmus: zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern
Jun 06, 2024 pm 12:33 PM
Verbesserter Erkennungsalgorithmus: zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern
Jun 06, 2024 pm 12:33 PM
01Ausblicksübersicht Derzeit ist es schwierig, ein angemessenes Gleichgewicht zwischen Detektionseffizienz und Detektionsergebnissen zu erreichen. Wir haben einen verbesserten YOLOv5-Algorithmus zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern entwickelt, der mehrschichtige Merkmalspyramiden, Multierkennungskopfstrategien und hybride Aufmerksamkeitsmodule verwendet, um die Wirkung des Zielerkennungsnetzwerks in optischen Fernerkundungsbildern zu verbessern. Laut SIMD-Datensatz ist der mAP des neuen Algorithmus 2,2 % besser als YOLOv5 und 8,48 % besser als YOLOX, wodurch ein besseres Gleichgewicht zwischen Erkennungsergebnissen und Geschwindigkeit erreicht wird. 02 Hintergrund und Motivation Mit der rasanten Entwicklung der Fernerkundungstechnologie wurden hochauflösende optische Fernerkundungsbilder verwendet, um viele Objekte auf der Erdoberfläche zu beschreiben, darunter Flugzeuge, Autos, Gebäude usw. Objekterkennung bei der Interpretation von Fernerkundungsbildern
 Anwendung von Algorithmen beim Aufbau einer 58-Porträt-Plattform
May 09, 2024 am 09:01 AM
Anwendung von Algorithmen beim Aufbau einer 58-Porträt-Plattform
May 09, 2024 am 09:01 AM
1. Hintergrund des Baus der 58-Portrait-Plattform Zunächst möchte ich Ihnen den Hintergrund des Baus der 58-Portrait-Plattform mitteilen. 1. Das traditionelle Denken der traditionellen Profiling-Plattform reicht nicht mehr aus. Der Aufbau einer Benutzer-Profiling-Plattform basiert auf Data-Warehouse-Modellierungsfunktionen, um Daten aus mehreren Geschäftsbereichen zu integrieren, um genaue Benutzerporträts zu erstellen Und schließlich muss es über Datenplattformfunktionen verfügen, um Benutzerprofildaten effizient zu speichern, abzufragen und zu teilen sowie Profildienste bereitzustellen. Der Hauptunterschied zwischen einer selbst erstellten Business-Profiling-Plattform und einer Middle-Office-Profiling-Plattform besteht darin, dass die selbst erstellte Profiling-Plattform einen einzelnen Geschäftsbereich bedient und bei Bedarf angepasst werden kann. Die Mid-Office-Plattform bedient mehrere Geschäftsbereiche und ist komplex Modellierung und bietet allgemeinere Funktionen. 2.58 Benutzerporträts vom Hintergrund der Porträtkonstruktion im Mittelbahnsteig 58
 Java-Datenstrukturen und -Algorithmen: ausführliche Erklärung
May 08, 2024 pm 10:12 PM
Java-Datenstrukturen und -Algorithmen: ausführliche Erklärung
May 08, 2024 pm 10:12 PM
Datenstrukturen und Algorithmen sind die Grundlage der Java-Entwicklung. In diesem Artikel werden die wichtigsten Datenstrukturen (wie Arrays, verknüpfte Listen, Bäume usw.) und Algorithmen (wie Sortier-, Such-, Diagrammalgorithmen usw.) ausführlich untersucht. Diese Strukturen werden anhand praktischer Beispiele veranschaulicht, darunter die Verwendung von Arrays zum Speichern von Bewertungen, verknüpfte Listen zum Verwalten von Einkaufslisten, Stapel zum Implementieren von Rekursionen, Warteschlangen zum Synchronisieren von Threads sowie Bäume und Hash-Tabellen für schnelle Suche und Authentifizierung. Wenn Sie diese Konzepte verstehen, können Sie effizienten und wartbaren Java-Code schreiben.
 PHP-Datenstruktur: Das Gleichgewicht der AVL-Bäume sorgt für eine effiziente und geordnete Datenstruktur
Jun 03, 2024 am 09:58 AM
PHP-Datenstruktur: Das Gleichgewicht der AVL-Bäume sorgt für eine effiziente und geordnete Datenstruktur
Jun 03, 2024 am 09:58 AM
Der AVL-Baum ist ein ausgewogener binärer Suchbaum, der schnelle und effiziente Datenoperationen gewährleistet. Um ein Gleichgewicht zu erreichen, führt es Links- und Rechtsdrehungen durch und passt Teilbäume an, die das Gleichgewicht verletzen. AVL-Bäume nutzen den Höhenausgleich, um sicherzustellen, dass die Höhe des Baums im Verhältnis zur Anzahl der Knoten immer klein ist, wodurch Suchoperationen mit logarithmischer Zeitkomplexität (O(logn)) erreicht werden und die Effizienz der Datenstruktur auch bei großen Datensätzen erhalten bleibt.
 Nachrichtenempfehlungsalgorithmus basierend auf globaler Diagrammverbesserung
Apr 08, 2024 pm 09:16 PM
Nachrichtenempfehlungsalgorithmus basierend auf globaler Diagrammverbesserung
Apr 08, 2024 pm 09:16 PM
Autor |. Rezensiert von Wang Hao |. Die Chonglou News App ist eine wichtige Möglichkeit für Menschen, Informationsquellen in ihrem täglichen Leben zu erhalten. Zu den beliebten ausländischen Nachrichten-Apps gehörten um 2010 Zite und Flipboard, während es sich bei den beliebten inländischen Nachrichten-Apps hauptsächlich um die vier großen Portale handelte. Mit der Beliebtheit der von Toutiao vertretenen Nachrichtenempfehlungsprodukte der neuen Ära sind Nachrichten-Apps in eine neue Ära eingetreten. Was Technologieunternehmen angeht, egal um welches Unternehmen es sich handelt, solange sie die hochentwickelte Nachrichtenempfehlungsalgorithmus-Technologie beherrschen, werden sie grundsätzlich die Initiative und Mitsprache auf technischer Ebene haben. Werfen wir heute einen Blick auf einen Beitrag zum RecSys2023 Best Long Paper Nomination Award – GoingBeyondLocal:GlobalGraph-EnhancedP



