为什么负数的取余计算各个编程语言结果不统一?
回复内容:
带符号整数的除法与余数 数学上都正确,这个定义本来就有好几个比如按

或者按

IEEE标准是则是
 ,然而round标准也有好几个。。。
,然而round标准也有好几个。。。如果round是IEEE默认的round to the nearest,从标准的角度似乎应该是3。。。但IEEE好像也没说其他的round标准不对。。。
PS:很多语言干脆提供了两个函数,rem和mod 就是商向0或负无穷方向取整的选择,c从c99开始规定向0取整,py则规定向负无穷取整,选择而已,无所谓对错 就算是相同语言不同编译器也会不一样的。
在我发现这个问题之后,每当我更新IDE/编译器的时候都会用我的测试程序跑一遍,看看是不是和上个版本有什么不同。
有的时候一些小改动很坑的。
PS:有时候也不行,不能保证测试结果是唯一的。 问题的关键在于商是向负无穷取值还是向0取值 -7/10=0....-7
or
-7/10=-1....3
其他语言我不清楚,貌似c11规定向0取值 关于负数的余数,楼上很多网友已经阐述了纯数学概念上的意义。我想从另一个角度说说我的看法。先明确一点:我们讨论的是“被除数”(分子)是负整数,而除数(分母)是正整数的情况。
先看一个例子: (-17) mod 5 =?
答案一: (-17) = (-3)*5 + (-2),所以余数是 -2 。
答案二: (-17) = (-4)*5 + (+3),所以余数是 +3 。
首先,从“纯数学”概念上说,两个答案都“对”,就好像解方程的时候出现“复数解”一样,也是一个解。所以各种编译器按照各自的逻辑来产生余数。
但是,从人类思维角度上说,“负数”的起源是因为“不足、欠缺”,使用负数是为了知道有多欠缺,然后去补救。从这个角度才能正确理解“负数的余数”的实际意义(区别于纯数学概念)。
打个比方,你和另外5个同学住在宿舍里,你很勤快,那5个人很懒,让你帮忙买早餐,比如说,油条、豆浆 …… 你提着他们的早餐回来,对他们说:“一共17块钱。”就是说,他们5个人一共欠你17元。平均每人给你 17/5=3.4元。
于是他们就翻箱倒柜 —— 不是没有钱,而是在找零钱,每人都要拿0.4元,嗯,各位看官不妨找找自己身上有没有4毛钱 …… 结果就是,都找不到零钱,怎么办?于是有两种办法:
办法一:每人给你3块钱,但是总共还欠你2块钱,余数= -2
办法二:每人给你4块钱,但是你要给回他们3块钱,余数 = +3
现在问题是:各位作为人类,倾向于采用哪一个办法?
上面说了,人类之所以使用负数,是为了知道“不足”,然后进行补救。现在既然欠了钱要还,我想那5位同学都会给你4块钱,倒不是说他们是为了给你3块钱跑腿费,而是他们想“了(liao)了(le)这笔账”,他们不想5个人 每人都欠你0.4元的人情(何况你还真的跑腿了),既然都还钱了,为什么还要留一笔“遗留问题”呢?
所以,从人类思维习惯和实际需要来说(再说一遍:区别于纯数学概念),无论被除数(分子)是正数还是负数,余数都应该取正数,这样才符合人类的思维习惯和实际需要。
题外话:就好像除数(分母)通常是正数一样,如果用一个负数来做除数(分母),人们会觉得很别扭,很难理解。
其实,如果允许余数可以是负数的话,那么 23%5 同样有两个答案,可以看作 +3,也可以是 -2,但我相信没有人会用 -2,第一反应肯定是用 +3 。
现在回到题主的问题: (-7)%10=? 是 +3 还是 -7 ?
如果说人话,就是:现在欠你7块钱,由10个人来还,怎么办?
办法一:每人还你一块钱,结果多出3块钱,余数=+3
办法二:每人还给你 0元,余数 = -7 ,结果最后,一切照旧,依然欠你7块钱 ……
数学语言说:向负无穷取值还是向0取值 ……
==========分割线==========分割线==========分割线==========分割线==========
说到这里,可能有人说,数学不是凭情感、看习惯的,数学是严谨的。
我非常赞同这个观点,对于数学这种推崇严密和严谨的科学,同样的操作数、同样的运算符,必然得到同样的运算结果。那么,余数这种“可正可负”的“双重标准”是致命的 Fatal Error ,会摧毁数学大殿的根基。试想一下,-7伏和+3伏是两个截然相反的脉冲信号,足以让航天飞机掉进茫茫大海了……
还是以 (-7)%10 为例。同余定理是数学的基础定理之一,中学生都懂,我们来看看:
13 %10 = 3
(13+10)%10= 3
(13+20)%10= 3
(13-10)%10= 3
(13-20)%10=(-7)%10=? —— 问题来了。
显然,根据余数定理,答案无疑就是+3 ,而不是 -7 。这与我的上述观点互相印证。
如果认为 (-7)%10=-7 的话,那么连中学生都懂的余数定理就不成立了,数学变得如此脆弱,如此不堪一击。
余数定理是计算机表示负数、补数的理论基础,那些编译器产生的混乱结果,恰恰说明这些编译器的开发者不懂得余数的概念和意义。毕竟,搞电脑和搞数学是不同的领域。 因为数学上一般不关心负数的余数,数论一般讨论的都是正整数。 可能是程序员没有区分开 取余和取模,百度一下取余,取模。仅供参考 说的好像各个编程语言内部是统一的一样。。
请题主先把cl、gcc、clang、cmake、tc等实现的各主要版本都实验一遍。。

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
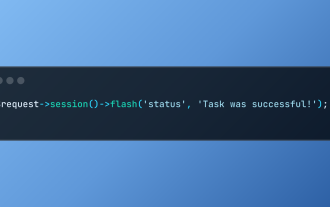 Arbeiten mit Flash -Sitzungsdaten in Laravel
Mar 12, 2025 pm 05:08 PM
Arbeiten mit Flash -Sitzungsdaten in Laravel
Mar 12, 2025 pm 05:08 PM
Laravel vereinfacht die Behandlung von temporären Sitzungsdaten mithilfe seiner intuitiven Flash -Methoden. Dies ist perfekt zum Anzeigen von kurzen Nachrichten, Warnungen oder Benachrichtigungen in Ihrer Anwendung. Die Daten bestehen nur für die nachfolgende Anfrage standardmäßig: $ Anfrage-
 Curl in PHP: So verwenden Sie die PHP -Curl -Erweiterung in REST -APIs
Mar 14, 2025 am 11:42 AM
Curl in PHP: So verwenden Sie die PHP -Curl -Erweiterung in REST -APIs
Mar 14, 2025 am 11:42 AM
Die PHP Client -URL -Erweiterung (CURL) ist ein leistungsstarkes Tool für Entwickler, das eine nahtlose Interaktion mit Remote -Servern und REST -APIs ermöglicht. Durch die Nutzung von Libcurl, einer angesehenen Bibliothek mit Multi-Protokoll-Dateien, erleichtert PHP Curl effiziente Execu
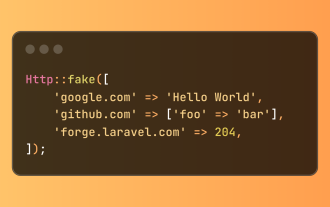 Vereinfachte HTTP -Reaktion verspottet in Laravel -Tests
Mar 12, 2025 pm 05:09 PM
Vereinfachte HTTP -Reaktion verspottet in Laravel -Tests
Mar 12, 2025 pm 05:09 PM
Laravel bietet eine kurze HTTP -Antwortsimulationssyntax und vereinfache HTTP -Interaktionstests. Dieser Ansatz reduziert die Code -Redundanz erheblich, während Ihre Testsimulation intuitiver wird. Die grundlegende Implementierung bietet eine Vielzahl von Verknüpfungen zum Antworttyp: Verwenden Sie Illuminate \ Support \ facades \ http; Http :: fake ([ 'Google.com' => 'Hallo Welt',, 'github.com' => ['foo' => 'bar'], 'Forge.laravel.com' =>
 12 Beste PHP -Chat -Skripte auf Codecanyon
Mar 13, 2025 pm 12:08 PM
12 Beste PHP -Chat -Skripte auf Codecanyon
Mar 13, 2025 pm 12:08 PM
Möchten Sie den dringlichsten Problemen Ihrer Kunden in Echtzeit und Sofortlösungen anbieten? Mit Live-Chat können Sie Echtzeitgespräche mit Kunden führen und ihre Probleme sofort lösen. Sie ermöglichen es Ihnen, Ihrem Brauch einen schnelleren Service zu bieten
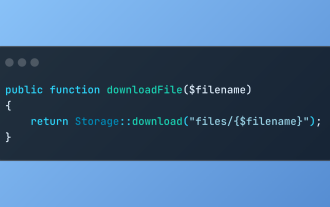 Datei -Downloads in Laravel mit Speicher :: Download ermitteln
Mar 06, 2025 am 02:22 AM
Datei -Downloads in Laravel mit Speicher :: Download ermitteln
Mar 06, 2025 am 02:22 AM
Die Speicher :: Download -Methode des Laravel -Frameworks bietet eine prägnante API für die sichere Bearbeitung von Datei -Downloads beim Verwalten von Abstraktionen des Dateispeichers. Hier ist ein Beispiel für die Verwendung von Storage :: download () im Beispiel -Controller:
 PHP -Protokollierung: Best Practices für die PHP -Protokollanalyse
Mar 10, 2025 pm 02:32 PM
PHP -Protokollierung: Best Practices für die PHP -Protokollanalyse
Mar 10, 2025 pm 02:32 PM
Die PHP -Protokollierung ist für die Überwachung und Debugie von Webanwendungen von wesentlicher Bedeutung sowie für das Erfassen kritischer Ereignisse, Fehler und Laufzeitverhalten. Es bietet wertvolle Einblicke in die Systemleistung, hilft bei der Identifizierung von Problemen und unterstützt eine schnellere Fehlerbehebung
 Erklären Sie das Konzept der späten statischen Bindung in PHP.
Mar 21, 2025 pm 01:33 PM
Erklären Sie das Konzept der späten statischen Bindung in PHP.
Mar 21, 2025 pm 01:33 PM
In Artikel wird die in PHP 5.3 eingeführte LSB -Bindung (LSB) erörtert, die die Laufzeitauflösung der statischen Methode ermöglicht, um eine flexiblere Vererbung zu erfordern. Die praktischen Anwendungen und potenziellen Perfo von LSB
 So registrieren und verwenden Sie Laravel -Dienstleister
Mar 07, 2025 am 01:18 AM
So registrieren und verwenden Sie Laravel -Dienstleister
Mar 07, 2025 am 01:18 AM
Der Service -Container und die Dienstleister von Laravel sind für seine Architektur von grundlegender Bedeutung. In diesem Artikel werden Servicecontainer untersucht, Details für die Erstellung, Registrierung, Registrierung und die praktische Nutzung mit Beispielen mit Beispielen untersucht. Wir beginnen mit einem Ove






