Insgesamt10000 bezogener Inhalt gefunden
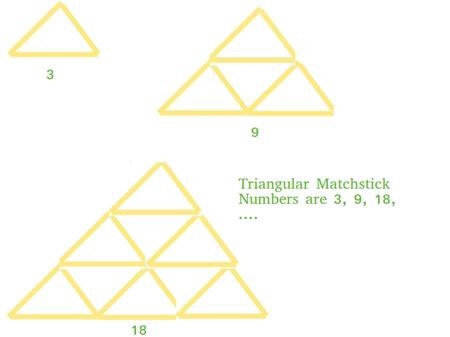
C/C++-Programm für dreieckige Streichholzzahlen?
Artikeleinführung:Ein Dreieck aus Streichhölzern, die so angeordnet sind, dass sie ein gleichseitiges Dreieck bilden, wird als dreieckige Streichholzzahl bezeichnet. Die Anzahl der Dreiecksübereinstimmungen ist die Anzahl der Übereinstimmungen, die erforderlich sind, um ein Übereinstimmungsdreieck zu bilden. In diesem Problem ist unsere Zahl die Basis X der Match-Pyramide. Unsere Aufgabe besteht darin, ein Programm zu schreiben, das die Gesamtzahl der Streichhölzer ausgibt, die erforderlich sind, um eine Pyramide aus Streichhölzern der Stufe x zu bilden. Schauen wir uns ein Beispiel an, um das Konzept klarer zu machen: Input:7Output:84 erklärt, dass es sich hierbei um eine Erweiterung trigonometrischer Zahlen handelt. Für eine ganze Zahl X sind die erforderlichen Streichhölzer dreimal so groß wie die Anzahl der
2023-09-23
Kommentar 0
1399

Ermitteln Sie mithilfe der C++-Programmierung die Anzahl möglicher Hypotenusen- und Flächenpaare eines rechtwinkligen Dreiecks
Artikeleinführung:In diesem Artikel erklären wir, wie man in C++ die Anzahl möglicher Paare aus Hypotenuse und Fläche ermittelt, die ein rechtwinkliges Dreieck bilden. Wir müssen die Anzahl aller möglichen Paare aus Hypotenuse und Fläche (H,A) bestimmen, die ein rechtwinkliges Dreieck bilden, wobei H die Hypotenuse und A die Fläche ist. In diesem Beispiel: ) 2…(1)Wir wissen auch, dass x2+y2=H2…(2)Löse (1)&(2)4*A2=x2(H2-x2)Löse die quadratische Gleichung in x2 und sei D( Diskriminante )>
2023-09-08
Kommentar 0
1093

So erstellen Sie 6 Dreiecke mit Java
Artikeleinführung:Um sechs Dreiecke in Java zu drucken, müssen Sie zunächst wissen, wie man Dreiecke ausgibt, z. B.: die Anzahl der Zeilen in der for-Schleife der ersten Ebene steuern, die Anzahl der Leerzeichen in der for-Schleife der zweiten und dritten Ebene steuern und Wenn Sie die Anzahl der * steuern, können Sie die Dreiecke ausdrucken. Schleifen Sie das Dreieck dann noch sechsmal, sodass Sie sechs Dreiecke haben.
2019-05-22
Kommentar 0
3427

Mindestanzahl an Seiten, die zur Bildung eines Dreiecks erforderlich sind
Artikeleinführung:Um die Mindestanzahl an Seiten zu bestimmen, die erforderlich ist, um ein Dreieck in einem Diagramm zu bilden, haben wir das Netzwerk zwischen den Mittelpunkten analysiert. Ein Dreieck kann gebildet werden, wenn drei Mittelpunkte ausschließlich oder auf Umwegen durch Kanten verbunden sind. Die Mindestanzahl der erforderlichen Kanten entspricht der Anzahl der Kanten, die in den bestehenden Verbindungen zwischen den drei Hubs verloren gehen. Indem wir uns die Grafik ansehen und die voneinander unabhängigen Mittelpunkte unterscheiden, können wir die Anzahl der zusätzlichen Seiten berechnen, die zur Bildung des Dreiecks erforderlich sind. Diese Methode unterscheidet sich, da nur minimale Anpassungen erforderlich sind, um eine Dreiecksbeziehung zwischen den Mittelpunkten im Diagramm zu erstellen. Verwendete Methoden Graph-Traversal-Methoden Graph-Traversal-Methoden, die verwendet werden, um die Mindestanzahl an Seiten zu ermitteln, die zum Erstellen eines Dreiecks erforderlich sind, umfassen die Untersuchung des Graphen mithilfe von Traversierungsberechnungen wie der Tiefensuche (DFS) oder der Breitensuche (BFS). aus jedem Diagramm
2023-08-25
Kommentar 0
929
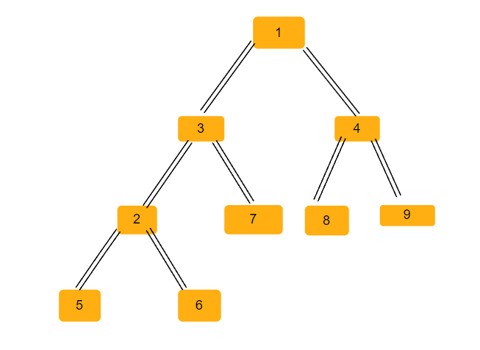
Die Anzahl gleichschenkliger Dreiecke in einem Binärbaum
Artikeleinführung:Ein Binärbaum ist eine Datenstruktur, in der jeder Knoten bis zu zwei untergeordnete Knoten haben kann. Diese Kinder werden linke Kinder bzw. rechte Kinder genannt. Angenommen, wir erhalten eine übergeordnete Array-Darstellung, Sie müssen diese verwenden, um einen Binärbaum zu erstellen. Ein Binärbaum kann mehrere gleichschenklige Dreiecke haben. Wir müssen die Gesamtzahl der möglichen gleichschenkligen Dreiecke in diesem Binärbaum ermitteln. In diesem Artikel werden wir verschiedene Techniken zur Lösung dieses Problems in C++ untersuchen. Wenn Sie das Problem verstehen, erhalten Sie ein übergeordnetes Array. Sie müssen es in Form eines Binärbaums darstellen, sodass der Array-Index den Wert des Baumknotens bildet und der Wert im Array den übergeordneten Knoten dieses bestimmten Index angibt. Beachten Sie, dass -1 immer das Root-Elternteil ist. Nachfolgend finden Sie ein Array und seine binäre Baumdarstellung. Parentarray=[0,-1,3,1,
2023-09-05
Kommentar 0
1096
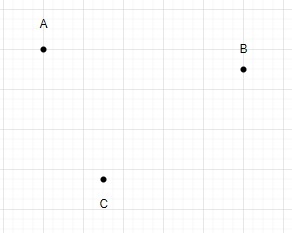
Wie viele Dreiecke gibt es, wenn nicht mehr als zwei Punkte in der Ebene kollinear sind?
Artikeleinführung:Sehen wir uns an, wie man bei n Punkten die Anzahl der Dreiecke auf einer Ebene zählt und die Anzahl der kollinearen Punkte auf nicht mehr als zwei begrenzt. Das Zählen der Anzahl von Dreiecken in einer Ebene mit nicht mehr als zwei kollinearen Punkten ist ein typisches Problem in der Computergeometrie, das in der Computergrafik, Bildverarbeitung und anderen Bereichen der Informatik Anwendung findet. Wenn beispielsweise in 3D-Grafiken ein 2D-Bild aus einer 3D-Szene erstellt wird, kann das Problem auftreten, Dreiecke in einer Ebene mit nicht mehr als zwei kollinearen Punkten zu berechnen. In diesem Fall kann der Prozess der Dreieckszählung verwendet werden, um zu bestimmen, wie viele Dreiecke im endgültigen 2D-Bild vorhanden sind, nachdem die 3D-Szene auf eine Ebene projiziert wurde. Dadurch können Sie die Komplexität der Szene bestimmen und die Rendergeschwindigkeit erhöhen. Bei der Bildverarbeitung möchten wir möglicherweise die Anzahl eindeutiger Objekte oder Formen in einem Bild zählen. Dieses Problem ist sehr groß
2023-09-05
Kommentar 0
1274

Java-Programm zur Anzeige des Floyd-Dreiecks
Artikeleinführung:Das Floyd-Dreieck ist eine beliebte rechtwinklige Dreiecksanordnung natürlicher Zahlen. Der Name geht auf den Gründer Robert W. Floyd zurück, einen berühmten Informatiker. Die Spitze des Dreiecks ist die Zahl 1, und jede weitere Zahl wird um 1 erhöht, wenn Sie in jeder Zeile nach unten gehen. In diesem Artikel erfahren Sie, wie Sie das Floyd-Dreieck mit einem Java-Programm anzeigen. Aber bevor wir mit der Java-Implementierung fortfahren, wollen wir uns mit Freuds Dreieck genauer befassen. Die erste Zeile enthält nur eine Zahl, nämlich 1 selbst, und jede nachfolgende Zeile enthält eine Zahl mehr als die vorherige Zeile. Ein Dreieck hat n Zeilen, wobei n eine beliebige positive ganze Zahl sein kann. Die Gesamtzahl der Werte im Dreieckwi
2023-09-15
Kommentar 0
1195

Wie man das gleichschenklige Dreieck von Yang Hui in PHP realisiert
Artikeleinführung:Das gleichschenklige Dreieck von Yang Hui ist eine der klassischen Figuren der Mathematik. Es hat nicht nur ein schönes Aussehen, sondern verfügt auch über gute mathematische Eigenschaften und wird in verschiedenen Bereichen häufig verwendet. In der Computerprogrammierung können wir auch verschiedene Sprachen verwenden, um den Algorithmus zur Erzeugung gleichschenkliger Dreiecke von Yang Hui zu implementieren. In diesem Artikel wird die Verwendung der PHP-Sprache zur Implementierung der Erzeugung gleichschenkliger Dreiecke von Yang Hui vorgestellt. 1. Das Konzept des gleichschenkligen Dreiecks von Yang Hui wird auch Pascal-Dreieck genannt. Es ist ein Dreieck, das aus Zahlen besteht. Schreiben Sie die Zahl 1 auf die Oberseite des Dreiecks Zahlen oben
2023-04-24
Kommentar 0
700

Die kleinste Dreieckszahl größer als p
Artikeleinführung:Wir besprechen Dreieckszahlen und wie man die kleinste Dreieckszahl findet, die nur größer als die angegebene Zahl „num“ ist. Wir werden zunächst diskutieren, was eine trigonometrische Zahl ist, und dann die kleinste trigonometrische Zahl finden, die größer als „num“ ist. Wir werden zwei verschiedene Ansätze für dasselbe Problem sehen. Bei der ersten Methode führen wir eine einfache Schleife aus, um die Ausgabe zu generieren, während wir bei der zweiten Methode zunächst eine allgemeine Formel zur Berechnung der erforderlichen Zahl generieren und diese Formel dann direkt anwenden, um die minimale Dreieckszahl zu erhalten. Problemstellung Wir müssen die kleinste Anzahl von Dreiecken finden, die nur größer als „num“ ist. Wir haben mehrere Kisten mit Bällen darin. Die Anzahl der Bälle, die die Box enthält, ist bei allen Boxen eine unterschiedliche Dreieckszahl. Die Kästchen sind von 1 bis n nummeriert. Wir müssen es aus der Box herausfinden
2023-09-20
Kommentar 0
1272


Wie mache ich die Kontrollecken eines Dreiecks mit FabricJS transparent?
Artikeleinführung:In diesem Tutorial erfahren Sie, wie Sie mit FabricJS die Kontrollecken eines Dreiecks transparent machen. Dreieck ist eine der verschiedenen Formen, die FabricJS bereitstellt. Um ein Dreieck zu erstellen, müssen wir eine Instanz der Fabric.Triangle-Klasse erstellen und sie der Leinwand hinzufügen. Mit der Eigenschaft transparentCorners können wir die Kontrollecken des Dreiecks transparent machen. Syntax newFabric.Triangle({TransparentCorners:Boolean}:Object) Parameter Optionen (optional) – Dieser Parameter ist ein Objekt, das unserem Dreieck zusätzliche Anpassungen ermöglicht. Mit diesem Parameter können Sie die Beziehung zwischen transparentCorners und ändern
2023-09-17
Kommentar 0
1584

Was ist das größte Ruero-Dreieck, das in ein Quadrat eingeschrieben ist, das ein rechtwinkliges Dreieck ist?
Artikeleinführung:Hier sehen wir die Fläche des größten Reuleaux-Dreiecks, eingeschrieben in ein Quadrat, das wiederum in ein rechtwinkliges Dreieck eingeschrieben ist. Die Seitenlänge des Quadrats ist „a“. Die Höhe eines Reuleaux-Dreiecks beträgt x. Die Basis des Dreiecks ist b, die Höhe ist l und die Hypotenuse ist h. Wir wissen, dass ein Quadrat, das in ein rechtwinkliges Dreieck mit der Höhe l und der Grundfläche b eingeschrieben ist, eine Seitenlänge hat – die Höhe eines Reuleaux-Dreiecks ist gleich a. Also a=x. Daher beträgt die Fläche eines Reuleaux-Dreiecks – Beispiel#include<iostream>#include<cmath>usingnamespacestd;fl
2023-09-04
Kommentar 0
1556

Gegenseitige Konvertierungsbeziehung trigonometrischer Funktionen
Artikeleinführung:Die Umrechnungsbeziehung zwischen trigonometrischen Funktionen sec (Sekanten) ist der Kehrwert des Sinuswerts csc (Kosekant) ist der Kehrwert des Kosinuswerts sin (Sinus) die Gegenseite/Hypotenuse des rechtwinkligen Dreiecks cos (Kosinus) das Glied/Hypotenuse von das rechtwinklige Dreieck Seitentan (Tangens) die gegenüberliegende Seite/angrenzende Seite eines rechtwinkligen Dreiecks cot (Kotangens) die angrenzende Seite/gegenüberliegende Seite eines rechtwinkligen Dreiecks und die Formel für zwei Winkel sin(A+B)=sinAcosB+cosAsinBsin(A-B) =sinAcosB-cosAsinBcos(A+ B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAta
2024-01-15
Kommentar 0
2724
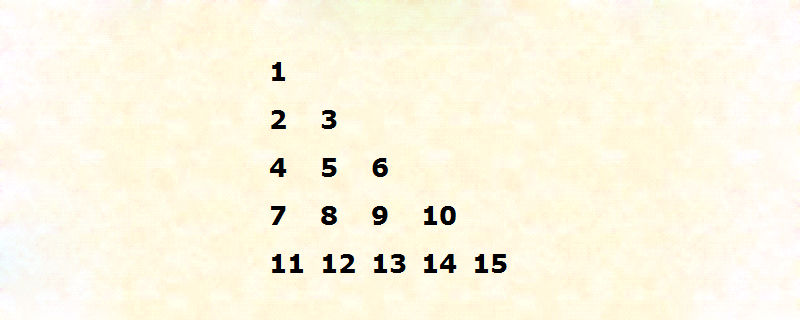
PHP implementiert Floyds Dreieck
Artikeleinführung:In diesem Artikel wird erläutert, wie Sie mit PHP die ersten n Zeilen des Floyd-Dreiecks generieren und anzeigen. (Verwenden Sie die Zeilen n=5 und n=11) Freuds Dreieck ist eine Menge rechtwinkliger dreieckiger natürlicher Zahlen, die im Informatikunterricht verwendet werden. Es ist nach Robert Floyd benannt. Es ist definiert als das Füllen der Reihen eines Dreiecks mit aufeinanderfolgenden Zahlen, beginnend von links
2019-03-22
Kommentar 0
3613

So implementieren Sie Dreiecke in CSS
Artikeleinführung:Methoden zum Implementieren von Dreiecken in CSS: 1. Verwenden Sie Rahmen, um Dreiecke zu implementieren. Verwenden Sie die Kombination aus transparenten Rändern und durchgezogenen Rändern, um Dreiecke in verschiedenen Richtungen und Größen zu erstellen. 2. Verwenden Sie Pseudoelemente, um Dreiecke zu implementieren, und verwenden Sie Pseudoelemente, um ein übergeordnetes Element zu erstellen Element, das das übergeordnete Element einnimmt. 3. Verwenden Sie das Transformationsattribut, um das Dreieck zu implementieren. Sie können Dreiecke mit unterschiedlichen Winkeln erstellen, indem Sie den Rotationswinkel anpassen das Dreieck, und Sie können Dreiecke mit unterschiedlichen Formen erstellen, indem Sie die Koordinaten mehrerer Punkte definieren.
2023-08-21
Kommentar 0
3804