Insgesamt10000 bezogener Inhalt gefunden
Minimale Spannbäume
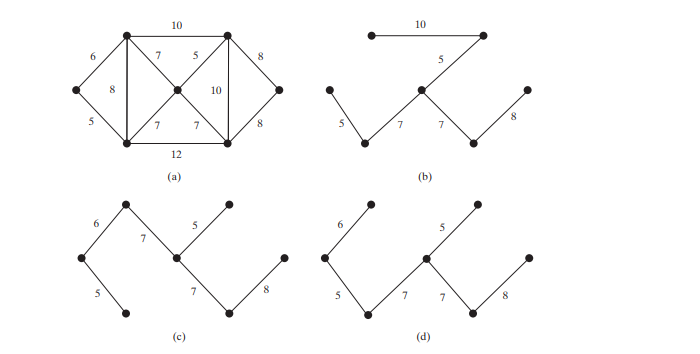
Artikeleinführung:Ein minimaler Spannbaum eines Diagramms ist ein Spannbaum mit den minimalen Gesamtgewichten.
Ein Graph kann viele Spannbäume haben. Angenommen, die Kanten sind gewichtet. Ein minimaler Spannbaum hat die minimalen Gesamtgewichte. Zum Beispiel die Bäume in Figuren
2024-09-06
Kommentar 0
1192

So schreiben Sie den Minimum-Spanning-Tree-Algorithmus mit C#
Artikeleinführung:So schreiben Sie mit C# den Minimum-Spanning-Tree-Algorithmus. Der Minimum-Spanning-Tree-Algorithmus ist ein wichtiger Algorithmus der Graphentheorie, der zur Lösung des Konnektivitätsproblems von Graphen verwendet wird. In der Informatik bezeichnet ein minimaler Spannbaum einen Spannbaum eines zusammenhängenden Graphen, bei dem die Summe der Gewichte aller Kanten des Spannbaums am kleinsten ist. In diesem Artikel wird erläutert, wie Sie mit C# den Minimal-Spanning-Tree-Algorithmus schreiben, und es werden spezifische Codebeispiele bereitgestellt. Zuerst müssen wir eine Diagrammdatenstruktur definieren, um das Problem darzustellen. In C# können Sie eine Adjazenzmatrix zur Darstellung eines Diagramms verwenden. Eine Adjazenzmatrix ist ein zweidimensionales Array, in dem jedes Element dargestellt wird
2023-09-19
Kommentar 0
728

Kruskals Minimum Spanning Tree-Algorithmus – Greedy-Algorithmus in C++
Artikeleinführung:Ein Spanning Tree ist ein Teilgraph eines gerichteten ungerichteten Graphen, der alle Knoten verbindet. In einem Diagramm können sich viele Spannbäume befinden. Der minimale Spannbaum (MST) in jedem Diagramm hat das gleiche oder ein geringeres Gewicht als alle anderen Spannbäume. Den Kanten des Spannbaums werden Gewichte zugewiesen, und die Summe ist das Gewicht, das jeder Kante zugewiesen wird. Da V die Anzahl der Eckpunkte im Diagramm ist, beträgt die Anzahl der Kanten des minimalen Spannbaums (V-1), wobei V die Anzahl der Kanten ist. Verwenden Sie den Kruskal-Algorithmus, um den minimalen Spannbaum zu finden. Alle Kanten sollten in nicht absteigender Reihenfolge nach Gewicht angeordnet werden. Wählen Sie die kleinste Seite. Wird keine Schlaufe gebildet, wird die Kante mit einbezogen. Schritt 2 sollte durchgeführt werden, bis der Spannbaum (V-1) Kanten hat. In diesem Fall wird uns gesagt, dass wir den Greedy-Ansatz verwenden sollen. Die gierige Option besteht darin, die Kante mit dem geringsten Gewicht zu wählen. Beispiel: Der minimale Spannbaum dieses Diagramms ist (9-1)=8
2023-08-28
Kommentar 0
1212

So implementieren Sie den Minimal-Spanning-Tree-Algorithmus mit Java
Artikeleinführung:So implementieren Sie den Minimum Spanning Tree-Algorithmus mit Java. Der Minimum Spanning Tree-Algorithmus ist ein klassisches Problem in der Graphentheorie, das zur Lösung des Minimum Spanning Tree eines gewichteten verbundenen Graphen verwendet wird. In diesem Artikel wird erläutert, wie Sie diesen Algorithmus mithilfe der Java-Sprache implementieren, und es werden spezifische Codebeispiele bereitgestellt. Problembeschreibung Gegeben ein zusammenhängender Graph G, in dem jede Kante ein Gewicht hat, muss ein minimaler Spannbaum T gefunden werden, so dass die Summe der Gewichte aller Kanten in T minimal ist. Prims Algorithmus Prims Algorithmus ist ein Greedy-Algorithmus, der zur Lösung des Minimum-Spanning-Tree-Problems verwendet wird. seine Grundidee
2023-09-21
Kommentar 0
1106

So verwenden Sie den Minimum Spanning Tree-Algorithmus in C++
Artikeleinführung:Verwendung des Minimum Spanning Tree-Algorithmus in C++. Minimum Spanning Tree (MST) ist ein wichtiges Konzept in der Graphentheorie. Es stellt die Teilmenge der Kanten dar, die alle Eckpunkte eines ungerichteten verbundenen Diagramms verbinden, und die Gewichte dieser Kanten betragen min. Es gibt viele Algorithmen, die zur Lösung des minimalen Spannbaums verwendet werden können, wie zum Beispiel der Prim-Algorithmus und der Kruskal-Algorithmus. In diesem Artikel wird erläutert, wie C++ zum Implementieren des Prim-Algorithmus und des Kruskal-Algorithmus verwendet wird, und es werden spezifische Codebeispiele gegeben. Prims Algorithmus ist a
2023-09-20
Kommentar 0
1266

So implementieren Sie den Minimum-Spanning-Tree-Algorithmus für Diagramme mit Java
Artikeleinführung:So verwenden Sie Java, um den Minimum Spanning Tree-Algorithmus für Diagramme zu implementieren. Konzepteinführung: Minimum Spanning Tree (MST) bezieht sich auf das Finden eines Baums in einem gewichteten gerichteten Diagramm oder ungerichteten Diagramm, sodass er alle Scheitelpunkte im Diagramm und die Summe der Gewichte enthält ist das Kleinste. Es gibt viele Minimum-Spanning-Tree-Algorithmen. Die beiden klassischsten Algorithmen sind der Prim-Algorithmus und der Kruskal-Algorithmus. Prims Algorithmus: Prims Algorithmus ist ein punktbasierter Greedy-Algorithmus, der an einem Scheitelpunkt beginnt und sich dann schrittweise erweitert
2023-09-19
Kommentar 0
1275

Boruvka-Algorithmus in C++ für minimalen Spanning Tree
Artikeleinführung:In der Graphentheorie ist das Finden des Minimum Spanning Tree (MST) eines verbundenen gewichteten Graphen ein häufiges Problem. MST ist die Teilmenge der Kanten des Diagramms, die alle Eckpunkte verbindet und das Gesamtkantengewicht minimiert. Ein effizienter Algorithmus zur Lösung dieses Problems ist der Boruvka-Algorithmus. Syntax structEdge{intsrc,dest,weight;};//Definethestructuretorepresentasubsetforunion-findstructSubset{intparent,rank;};Algorithmus Lassen Sie uns nun die Schritte skizzieren, die mit dem Boruvka-Algorithmus verbunden sind, um den minimalen Spanning Tree zu finden. − Initialisieren Sie den MST mit der leeren Menge . für jeden Scheitelpunkt
2023-08-27
Kommentar 0
873

Wie kann man das Minimum-Spanning-Tree-Problem in PHP mithilfe der Divide-and-Conquer-Methode lösen und die optimale Lösung erhalten?
Artikeleinführung:Wie kann man das Minimum-Spanning-Tree-Problem in PHP mithilfe der Divide-and-Conquer-Methode lösen und die optimale Lösung erhalten? Der minimale Spannbaum ist ein klassisches Problem der Graphentheorie. Ziel ist es, eine Teilmenge aller Eckpunkte in einem verbundenen Diagramm zu finden und die Kanten so zu verbinden, dass die Teilmenge einen Baum bildet und die Summe der Gewichte aller Kanten am kleinsten ist. Bei der Divide-and-Conquer-Methode geht es darum, ein großes Problem in mehrere Teilprobleme zu zerlegen, die Teilprobleme dann einzeln zu lösen und schließlich die Ergebnisse zusammenzuführen. Die Verwendung der Divide-and-Conquer-Methode zur Lösung des Minimum-Spanning-Tree-Problems in PHP kann durch Befolgen der folgenden Schritte erreicht werden. Definieren Sie die Datenstruktur des Diagramms:
2023-09-19
Kommentar 0
918

Wie kann man den Greedy-Algorithmus verwenden, um die optimale Lösung des Minimum-Spanning-Tree-Problems in PHP zu erreichen?
Artikeleinführung:Wie kann man den Greedy-Algorithmus verwenden, um die optimale Lösung des Minimum-Spanning-Tree-Problems in PHP zu erreichen? Das Problem des minimalen Spannbaums (MinimumSpanningTree) besteht darin, einen Teilbaum in einem verbundenen ungerichteten Diagramm zu finden, sodass dieser Teilbaum alle Scheitelpunkte im Diagramm enthält und die Summe der Gewichte aller Kanten am kleinsten ist. Der Greedy-Algorithmus ist eine der gängigen Methoden zur Lösung dieses Problems. Er findet nach und nach die globale optimale Lösung, indem er jedes Mal die aktuell optimale Lösung auswählt. Zuerst müssen wir eine Graphklasse definieren, um die Struktur des Graphen und die Gewichte der Kanten zu speichern. Das Folgende ist ein Beispiel dafür
2023-09-19
Kommentar 0
1030

Warum schlägt der Minimum-Spanning-Tree-Algorithmus von Prim und Kruskal in gerichteten Graphen fehl?
Artikeleinführung:Die Prim-Methode und der Kruskal-Algorithmus sind zwei gängige Methoden zum Auffinden von MST (Minimum Spanning Tree) in ungerichteten Graphen. Diese Techniken können jedoch keine korrekte MST für gerichtete Graphen erzeugen. Dies liegt daran, dass gerichtete Graphen nicht den Grundannahmen und Methoden der Algorithmen von Prim und Kruskal entsprechen. Der Algorithmus von Prim Zunächst gibt es den Algorithmus von Prim, der das gierige Hinzufügen von Kanten zu einem expandierenden minimalen Spannbaum beinhaltet, bis alle Eckpunkte abgedeckt sind. Scheitelpunkte innerhalb des MST werden über die Kante mit dem geringsten Gewicht mit Scheitelpunkten außerhalb des MST verbunden. Da sich alle Kanten in einem ungerichteten Graphen in jede Richtung bewegen können, ist der kürzeste Weg vom MST zu externen Eckpunkten leicht zu finden. Allerdings zeigen in einem gerichteten Graphen die Kanten immer in eine Richtung und es kann sein, dass es keine gerade Linie gibt
2023-09-02
Kommentar 0
660
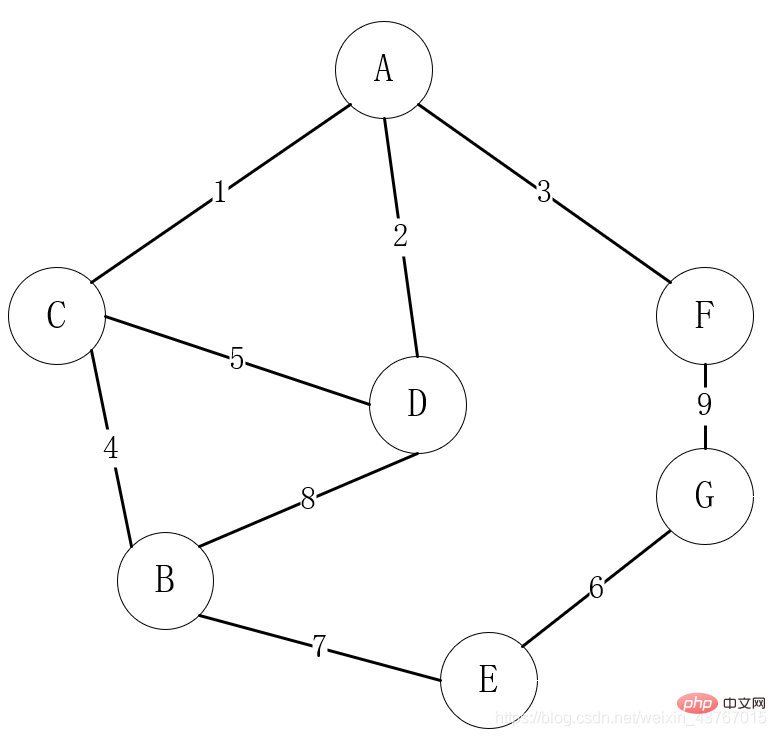
So finden Sie den minimalen Spanning Tree in Java
Artikeleinführung:1 Überblick über den minimalen Spanning Tree Spanning Tree (SpanningTree): Der Spanning Tree eines verbundenen Graphen bezieht sich auf einen verbundenen Untergraphen, der alle n Scheitelpunkte im Graphen enthält, aber nur n-1 Kanten, die ausreichen, um einen Baum zu bilden. Ein Spannbaum mit n Eckpunkten hat nur n-1 Kanten. Wenn dem Spannbaum eine weitere Kante hinzugefügt wird, bildet er definitiv einen Kreis. Minimaler Spannbaum (MinimumSpanningTree): Unter allen Spannbäumen in einem verbundenen Diagramm wird das Gewicht aller Kanten und der kleinste Spannbaum als minimaler Spannbaum bezeichnet. Im Leben wird am häufigsten die grafische Struktur verwendet. Beispielsweise können Dörfer bei der Auswahl üblicher Kommunikationsnetze als Eckpunkte betrachtet werden. Wenn es einen Kommunikationspfad zwischen Dörfern gibt, wird dieser als Kante oder Bogen zwischen zwei Punkten gezählt.
2023-04-29
Kommentar 0
726

Detaillierte Erklärung des Minimum Spanning Tree-Algorithmus in PHP
Artikeleinführung:Detaillierte Erläuterung des Minimum Spanning Tree-Algorithmus in PHP Minimum Spanning Tree (kurz MST) ist ein wichtiges Konzept in der Graphentheorie, das zur Lösung des Problems der Auswahl der Kante mit minimalem Gewicht eines verbundenen Diagramms verwendet wird. In der PHP-Sprache können wir diese Funktion durch einige klassische Minimum-Spanning-Tree-Algorithmen implementieren. In diesem Artikel werden zwei häufig verwendete Minimum-Spanning-Tree-Algorithmen im Detail vorgestellt: der Algorithmus von Prim und der Algorithmus von Kruskal, und es werden entsprechende PHP-Codebeispiele gegeben. 1. Prim-Algorithmus Der Prim-Algorithmus ist ein
2023-07-07
Kommentar 0
1300

Ausführliche Erläuterung von Beispielen für minimal aufspannende Bäume
Artikeleinführung:Der Artikel ist ein Nachdruck aus: Minimum Spanning Tree-Prim-Algorithmus und Kruskal-Algorithmus
Der Spannbaum eines Graphen ist sein azyklisch verbundener Untergraph, der alle Eckpunkte enthält, und der minimale Spannbaum eines gewichteten Graphen ist sein Spannbaum mit dem kleinsten Gewicht.
Prims Algorithmus
Eine kurze Beschreibung des Algorithmus
1).Eingabe: ein gewichteter verbundener Graph, in dem die Scheitelpunktmenge V und die Kantenmenge E ist;
2).Initialisierung: Vnew = {x}, wobei x ein beliebiger Knoten (Startpunkt) in der Menge V ist, Enew = {}, leer ist;
3). Wiederholen Sie die folgenden Vorgänge bis Vnew
2017-06-25
Kommentar 0
3466

Fragen Sie das Mindestgewicht im Teilbaum ab Knoten X und höchstens Abstand D ab
Artikeleinführung:Bei der Computerprogrammierung ist es manchmal erforderlich, das Mindestgewicht eines Teilbaums zu ermitteln, der von einem bestimmten Knoten stammt, vorausgesetzt, der Teilbaum darf keine Knoten enthalten, die mehr als D Einheiten vom angegebenen Knoten entfernt sind. Dieses Problem tritt in verschiedenen Bereichen und Anwendungen auf, darunter in der Graphentheorie, baumbasierten Algorithmen und der Netzwerkoptimierung. Ein Teilbaum ist eine Teilmenge einer größeren Baumstruktur, wobei der angegebene Knoten als Wurzelknoten des Teilbaums dient. Ein Teilbaum enthält alle Nachkommen des Wurzelknotens und deren Verbindungskanten. Die Gewichtung eines Knotens bezieht sich auf einen bestimmten, diesem Knoten zugewiesenen Wert, der seine Wichtigkeit, Wichtigkeit oder andere relevante Metriken darstellen kann. Bei diesem Problem besteht das Ziel darin, das Mindestgewicht aller Knoten in einem Teilbaum zu ermitteln und gleichzeitig den Teilbaum auf Knoten zu beschränken, die höchstens D Einheiten vom Wurzelknoten entfernt sind. Im folgenden Artikel werden wir uns mit der Komplexität des Minings von Mindestgewichten aus Teilbäumen befassen
2023-08-25
Kommentar 0
1470

Der Generierungsprozess des Entscheidungsbaums hängt mit dem ID3-Algorithmus zusammen
Artikeleinführung:Der ID3-Algorithmus ist ein klassischer Algorithmus zur Generierung von Entscheidungsbäumen, der 1986 von Ross Quinlan vorgeschlagen wurde. Es wählt die besten Features als Teilungsknoten aus, indem es den Informationsgewinn jedes Features berechnet. Der ID3-Algorithmus wird häufig in den Bereichen maschinelles Lernen und Data Mining eingesetzt und spielt insbesondere bei Klassifizierungsaufgaben eine wichtige Rolle. Seine Verwendung kann die Genauigkeit und Interpretierbarkeit des Modells verbessern und gleichzeitig komplexe Datensätze mit mehreren Funktionen und Kategorien verarbeiten. Ein Entscheidungsbaum ist eine Baumstruktur, die zur Klassifizierung oder Regression verwendet wird. Es besteht aus Knoten und Kanten. Knoten stellen Merkmale oder Attribute dar, und Kanten stellen mögliche Werte oder Entscheidungen dar. Der Wurzelknoten stellt die wichtigsten Merkmale dar und die Blattknoten stellen das endgültige Klassifizierungsergebnis dar. Der Entscheidungsbaum bestimmt das Klassifizierungsergebnis, indem er die Merkmalswerte jedes Mal schrittweise beurteilt
2024-01-22
Kommentar 0
1142
PHP树的深度编历生成迷宫及A*自动寻路算法实例分析
Artikeleinführung:PHP树的深度编历生成迷宫及A*自动寻路算法实例分析。PHP树的深度编历生成迷宫及A*自动寻路算法实例分析 这篇文章主要介绍了PHP树的深度编历生成迷宫及A*自动寻路算法,实例分析了php实现A*寻
2016-06-13
Kommentar 0
1081












