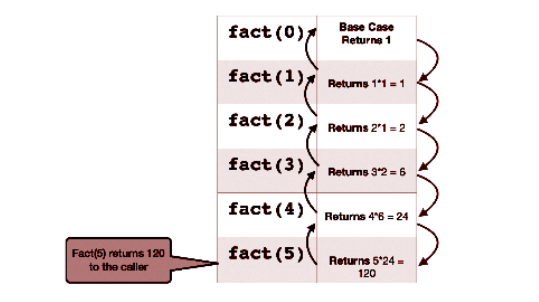
Artikeleinführung：Definition der Rekursion: Rekursion ist eine Methode, die sich selbst aufruft. Eine Methode ist rekursiv, wenn sie einen Aufruf an sich selbst enthält. Klassisches Beispiel: Die faktorielle Berechnung ist ein klassisches Beispiel für Rekursion. Die Fakultät einer Zahl? ist das Produkt von

2024-08-31 Kommentar 0  744

Artikeleinführung：PHP递归创建多级目录，php递归。PHP递归创建多级目录，php递归 我的第一个感觉就是用递归创建，具体思路如下： function Directory($dir){ if(is_dir($dir) || @mkdir($dir,0777)){ //查看目

2016-06-13 Kommentar 0  1083

Artikeleinführung：Rekursive Definition und Optimierung: Rekursiv: Eine Funktion ruft sich intern auf, um schwierige Probleme zu lösen, die in kleinere Teilprobleme zerlegt werden können. Schwanzrekursion: Die Funktion führt alle Berechnungen durch, bevor sie einen rekursiven Aufruf durchführt, der in eine Schleife optimiert werden kann. Optimierungsbedingung für die Schwanzrekursion: Der rekursive Aufruf ist die letzte Operation. Die rekursiven Aufrufparameter sind dieselben wie die ursprünglichen Aufrufparameter. Praktisches Beispiel: Fakultät berechnen: Die Hilfsfunktion Factorial_helper implementiert die Schwanzrekursionsoptimierung, eliminiert den Aufrufstapel und verbessert die Effizienz. Fibonacci-Zahlen berechnen: Die Schwanzrekursivfunktion fibonacci_helper nutzt die Optimierung, um Fibonacci-Zahlen effizient zu berechnen.

2024-05-03 Kommentar 0  913

Artikeleinführung：php实现无限级分类查询（递归、非递归），分类查询递归。php实现无限级分类查询（递归、非递归），分类查询递归 做PHP这么长时间，发现后台管理系统不可少的一个应用模块就是对栏目的分类，一

2016-06-13 Kommentar 0  1381

Artikeleinführung：约瑟夫环递归和非递归解法

2016-05-25 Kommentar 0  1250

Artikeleinführung：这篇文章主要介绍了php递归使用示例(php递归函数),包括递归获得角色ID字符串、递归获取级联角色信息数组、通过父角色的id获取子角色信息,需要的朋友可以参考下

2016-06-06 Kommentar 0  1088

Artikeleinführung：Rekursion ist eine Technik, bei der sich eine Funktion selbst aufruft, aber die Nachteile eines Stapelüberlaufs und einer Ineffizienz aufweist. Zu den Alternativen gehören: Tail-Recursion-Optimierung, bei der der Compiler rekursive Aufrufe in Schleifen optimiert, die Schleifen anstelle von Rekursion und Coroutinen verwenden, die das Anhalten und Fortsetzen der Ausführung ermöglichen und so rekursives Verhalten simulieren.

2024-05-01 Kommentar 0  1036

Artikeleinführung：Rekursion ist eine Programmiertechnik, bei der sich eine Funktion selbst aufruft. In C++ gibt es zwei gängige Formen: direkte Rekursion und indirekte Rekursion. Um eine Rekursion zu implementieren, muss die Funktion grundlegende Bedingungen und rekursive Aufrufe erfüllen. Im tatsächlichen Fall wird die rekursive Berechnung der Fakultät verwendet. Die Grundbedingung ist, dass n zurückgegeben wird, wenn n 0 ist. Der rekursive Aufruf ist die Funktion, die mit n multipliziert wird und sich selbst aufruft, wodurch n dekrementiert wird.

2024-05-04 Kommentar 0  493

Artikeleinführung：Der rekursive Algorithmus löst strukturierte Probleme durch den Selbstaufruf von Funktionen. Der Vorteil besteht darin, dass er einfach und leicht zu verstehen ist. Der Nachteil besteht jedoch darin, dass er weniger effizient ist und einen Stapelüberlauf verursachen kann Der Vorteil der Stapeldatenstruktur besteht darin, dass sie effizienter ist und einen Stapelüberlauf vermeidet. Der Nachteil besteht darin, dass der Code möglicherweise komplexer ist. Die Wahl zwischen rekursiv und nicht rekursiv hängt vom Problem und den spezifischen Einschränkungen der Implementierung ab.

2024-04-22 Kommentar 0  1177

Artikeleinführung：Bei der Funktionsrekursion ruft sich eine Funktion selbst auf und bietet eine effektive Möglichkeit, komplexe Probleme zu lösen, indem das Problem in Unterprobleme zerlegt wird. Es ist wichtig, die Rekursion zu optimieren, um einen Stapelüberlauf zu vermeiden. Zu den gängigen Optimierungstechniken gehören: Begrenzen der Rekursionstiefe, Verwenden der Tail-Rekursionsoptimierung, Verwenden von Memos, um doppelte Berechnungen zu vermeiden

2024-05-02 Kommentar 0  1278

Artikeleinführung：Die Standardrekursion in C++ verursacht Stapelplatz- und Zeitaufwand, die Tail-Rekursion jedoch nicht. Zu den Optimierungspraktiken gehören die Identifizierung von Tail-Rekursionen, die Konvertierung in Tail-Rekursionen und die Aktivierung der Compiler-Unterstützung. Die Tail-Rekursion ist leistungsfähiger als die Standardrekursion, da sie die Erstellung zusätzlicher Aktivitätsdatensätze und den damit verbundenen Overhead vermeidet.

2024-05-04 Kommentar 0  592

Artikeleinführung：Rekursive Funktionen können zum Durchlaufen einer Baumstruktur verwendet werden. Das Grundprinzip besteht darin, dass sich die Funktion so lange selbst aufruft und verschiedene Parameterwerte übergibt, bis der Basisfall die Rekursion beendet. In der Praxis folgt die rekursive Funktion zum Durchlaufen eines Binärbaums dem folgenden Prozess: Wenn der aktuelle Knoten leer ist, wird der Wert des aktuellen Knotens rekursiv durchquert. Die Komplexität des Algorithmus hängt von der Struktur des Baums ab. Für einen vollständigen Binärbaum beträgt die Anzahl der rekursiven Aufrufe 2n. Beachten Sie, dass Sie sicherstellen sollten, dass der Basisfall den rekursiven Prozess beendet, und die Rekursion mit Vorsicht verwenden sollten, um Stapelüberläufe zu vermeiden.

2024-05-04 Kommentar 0  569

Artikeleinführung：php实现无限级分类（递归方法），php递归。php实现无限级分类（递归方法），php递归 相信很多学php的很多小伙伴都会尝试做一个网上商城作为提升自己技术的一种途径。各种对商品分

2016-06-13 Kommentar 0  986

Artikeleinführung：Rekursion ist der Prozess, bei dem eine Funktion sich selbst aufruft. Die zeitliche Komplexität der Rekursion kann durch Berechnen der Anzahl rekursiver Aufrufe analysiert werden. Beispielsweise ist die Fakultätsfunktion O(n^2) und die rekursive Funktion des n-ten Elements der Fibonacci-Folge ist O(φ^n). wobei φ der Goldene Schnitt ist.

2024-05-04 Kommentar 0  558

Artikeleinführung：Tail-Rekursionsoptimierung in PythonIn Python führt der Versuch, die Tail-Rekursion zu implementieren, oft zu einem Fehler „Maximale Rekursionstiefe überschritten“.

2024-12-09 Kommentar 0  481

Artikeleinführung：Zu den häufigsten Fehlern bei rekursiven Funktionen gehören die unendliche Rekursion, die dazu führt, dass die Funktion sich selbst unendlich aufruft; dieser Fehler tritt auf, wenn es zu viele rekursive Aufrufe gibt, und logische Fehler, bei denen eine rekursive Funktion falsche Antworten liefern kann. Im tatsächlichen Fall wird eine rekursive Berechnung der Fakultät verwendet, und die Definition der Fakultät wird verwendet, um das faktorielle Problem mit größerem Maßstab in ein Problem mit kleinerem Maßstab umzuwandeln. Daher sollten diese Fehler bei der Verwendung der Rekursion vermieden werden, um die Korrektheit und Effizienz der Funktion sicherzustellen.

2024-04-30 Kommentar 0  465

Artikeleinführung：Strategien zur Vermeidung einer Rekursionsexplosion: Schwanzrekursionsoptimierung: Rekursive Aufrufe am Ende von Funktionen in Schleifen umwandeln. Merken: Berechnete Ergebnisse speichern, um wiederholte Anrufe zu vermeiden. Iterative Implementierung: Verwenden Sie Schleifen statt rekursiver Aufrufe.

2024-04-22 Kommentar 0  1270

Artikeleinführung：Einleitung 1 Der Vorgang, bei dem sich eine Funktion selbst aufruft, wird als Rekursion bezeichnet Die entsprechende Funktion wird als rekursive Funktion bezeichnet. Da Computerprogrammierung eine grundlegende Anwendung der Mathematik ist, sei es so Wir versuchen zuerst, es zu verstehen

2024-08-25 Kommentar 0  687

Artikeleinführung：Die Strategie zur Optimierung der Schwanzrekursion reduziert effektiv die Tiefe des Funktionsaufrufstapels und verhindert einen Stapelüberlauf, indem sie Schwanzrekursionsaufrufe in Schleifen umwandelt. Zu den Optimierungsstrategien gehören: Tail-Rekursion erkennen: Überprüfen Sie, ob Tail-rekursive Aufrufe in der Funktion vorhanden sind. Konvertieren Sie Funktionen in Schleifen: Verwenden Sie Schleifen anstelle von endrekursiven Aufrufen und pflegen Sie einen Stapel, um den Zwischenzustand zu speichern.

2024-04-17 Kommentar 0  676

Artikeleinführung：php递归遍历多维数组的方法，php递归多维数组。php递归遍历多维数组的方法，php递归多维数组 本文实例讲述了php递归遍历多维数组的方法。分享给大家供大家参考。具体如下： phpfunctio

2016-06-13 Kommentar 0  1152