Kurs Dazwischenliegend  11342

Kurseinführung：„Selbststudium IT-Netzwerk-Linux-Lastausgleich-Video-Tutorial“ implementiert hauptsächlich den Linux-Lastausgleich durch Ausführen von Skriptvorgängen im Web, LVS und Linux unter Nagin.

Kurs Fortschrittlich  17646

Kurseinführung：„Shang Xuetang MySQL Video Tutorial“ führt Sie in den Prozess von der Installation bis zur Verwendung der MySQL-Datenbank ein und stellt die spezifischen Vorgänge jedes Links im Detail vor.

Kurs Fortschrittlich  11353

Kurseinführung：„Brothers Band Front-End-Beispiel-Display-Video-Tutorial“ stellt jedem Beispiele für HTML5- und CSS3-Technologien vor, damit jeder die Verwendung von HTML5 und CSS3 besser beherrschen kann.

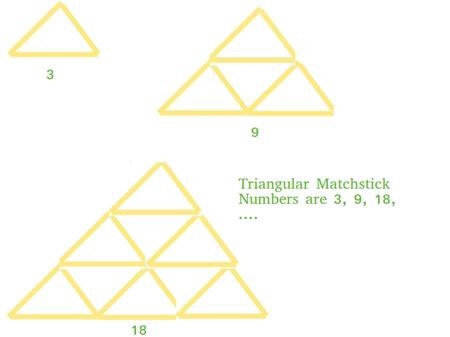
Kurseinführung：Ein Dreieck aus Streichhölzern, die so angeordnet sind, dass sie ein gleichseitiges Dreieck bilden, wird als dreieckige Streichholzzahl bezeichnet. Die Anzahl der Dreiecksübereinstimmungen ist die Anzahl der Übereinstimmungen, die erforderlich sind, um ein Übereinstimmungsdreieck zu bilden. In diesem Problem ist unsere Zahl die Basis X der Match-Pyramide. Unsere Aufgabe besteht darin, ein Programm zu schreiben, das die Gesamtzahl der Streichhölzer ausgibt, die erforderlich sind, um eine Pyramide aus Streichhölzern der Stufe x zu bilden. Schauen wir uns ein Beispiel an, um das Konzept klarer zu machen: Input:7Output:84 erklärt, dass es sich hierbei um eine Erweiterung trigonometrischer Zahlen handelt. Für eine ganze Zahl X sind die erforderlichen Streichhölzer dreimal so groß wie die Anzahl der

2023-09-23 Kommentar 0  1410

Kurseinführung：In diesem Artikel erklären wir, wie man in C++ die Anzahl möglicher Paare aus Hypotenuse und Fläche ermittelt, die ein rechtwinkliges Dreieck bilden. Wir müssen die Anzahl aller möglichen Paare aus Hypotenuse und Fläche (H,A) bestimmen, die ein rechtwinkliges Dreieck bilden, wobei H die Hypotenuse und A die Fläche ist. In diesem Beispiel: ) 2​​…(1)Wir wissen auch, dass x2+y2=H2…(2)Löse (1)&(2)4*A2=x2(H2-x2)Löse die quadratische Gleichung in x2 und sei D( Diskriminante )>

2023-09-08 Kommentar 0  1109

Kurseinführung：Um die Mindestanzahl an Seiten zu bestimmen, die erforderlich ist, um ein Dreieck in einem Diagramm zu bilden, haben wir das Netzwerk zwischen den Mittelpunkten analysiert. Ein Dreieck kann gebildet werden, wenn drei Mittelpunkte ausschließlich oder auf Umwegen durch Kanten verbunden sind. Die Mindestanzahl der erforderlichen Kanten entspricht der Anzahl der Kanten, die in den bestehenden Verbindungen zwischen den drei Hubs verloren gehen. Indem wir uns die Grafik ansehen und die voneinander unabhängigen Mittelpunkte unterscheiden, können wir die Anzahl der zusätzlichen Seiten berechnen, die zur Bildung des Dreiecks erforderlich sind. Diese Methode unterscheidet sich, da nur minimale Anpassungen erforderlich sind, um eine Dreiecksbeziehung zwischen den Mittelpunkten im Diagramm zu erstellen. Verwendete Methoden Graph-Traversal-Methoden Graph-Traversal-Methoden, die verwendet werden, um die Mindestanzahl an Seiten zu ermitteln, die zum Erstellen eines Dreiecks erforderlich sind, umfassen die Untersuchung des Graphen mithilfe von Traversierungsberechnungen wie der Tiefensuche (DFS) oder der Breitensuche (BFS). aus jedem Diagramm

2023-08-25 Kommentar 0  939

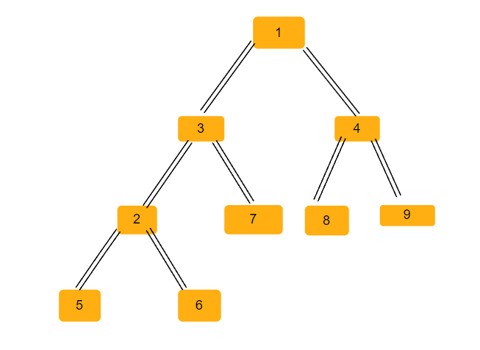
Kurseinführung：Ein Binärbaum ist eine Datenstruktur, in der jeder Knoten bis zu zwei untergeordnete Knoten haben kann. Diese Kinder werden linke Kinder bzw. rechte Kinder genannt. Angenommen, wir erhalten eine übergeordnete Array-Darstellung, Sie müssen diese verwenden, um einen Binärbaum zu erstellen. Ein Binärbaum kann mehrere gleichschenklige Dreiecke haben. Wir müssen die Gesamtzahl der möglichen gleichschenkligen Dreiecke in diesem Binärbaum ermitteln. In diesem Artikel werden wir verschiedene Techniken zur Lösung dieses Problems in C++ untersuchen. Wenn Sie das Problem verstehen, erhalten Sie ein übergeordnetes Array. Sie müssen es in Form eines Binärbaums darstellen, sodass der Array-Index den Wert des Baumknotens bildet und der Wert im Array den übergeordneten Knoten dieses bestimmten Index angibt. Beachten Sie, dass -1 immer das Root-Elternteil ist. Nachfolgend finden Sie ein Array und seine binäre Baumdarstellung. Parentarray=[0,-1,3,1,

2023-09-05 Kommentar 0  1104

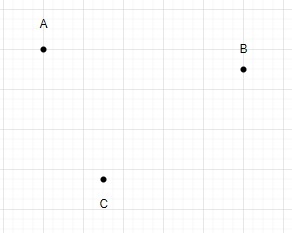
Kurseinführung：Sehen wir uns an, wie man bei n Punkten die Anzahl der Dreiecke auf einer Ebene zählt und die Anzahl der kollinearen Punkte auf nicht mehr als zwei begrenzt. Das Zählen der Anzahl von Dreiecken in einer Ebene mit nicht mehr als zwei kollinearen Punkten ist ein typisches Problem in der Computergeometrie, das in der Computergrafik, Bildverarbeitung und anderen Bereichen der Informatik Anwendung findet. Wenn beispielsweise in 3D-Grafiken ein 2D-Bild aus einer 3D-Szene erstellt wird, kann das Problem auftreten, Dreiecke in einer Ebene mit nicht mehr als zwei kollinearen Punkten zu berechnen. In diesem Fall kann der Prozess der Dreieckszählung verwendet werden, um zu bestimmen, wie viele Dreiecke im endgültigen 2D-Bild vorhanden sind, nachdem die 3D-Szene auf eine Ebene projiziert wurde. Dadurch können Sie die Komplexität der Szene bestimmen und die Rendergeschwindigkeit erhöhen. Bei der Bildverarbeitung möchten wir möglicherweise die Anzahl eindeutiger Objekte oder Formen in einem Bild zählen. Dieses Problem ist sehr groß

2023-09-05 Kommentar 0  1286