 Software Tutorial
Software Tutorial
 Computer Software
Computer Software
 Detailed method for finding the roots of a quadratic equation using Geometry Sketchpad
Detailed method for finding the roots of a quadratic equation using Geometry Sketchpad
Detailed method for finding the roots of a quadratic equation using Geometry Sketchpad
Geometry Sketchpad Find the roots of quadratic equations. Solving quadratic equations is a common problem in mathematics. Geometry Sketchpad, a geometric drawing software, provides an effective way to solve such equations. In this article, PHP editor Baicao will introduce in detail the complete process of using the geometric sketchpad to find the roots of a quadratic equation of one variable. This article will demonstrate step by step how to construct the graph of an equation, exploit geometric properties, and derive the exact values of the roots. Readers are advised to read the following details carefully to master the specific steps and techniques of this method.
Step 1: Open the software and establish three parameters. Click [Data] in the upper menu and select [New Parameter] from the pop-up drop-down menu. In the small window that pops up, change t1 to a, select unitless, and default the value, then click OK. In the same way, establish the other two parameters b and parameter c. Let their values be 1 first, and then you can change the values of the parameters at will.
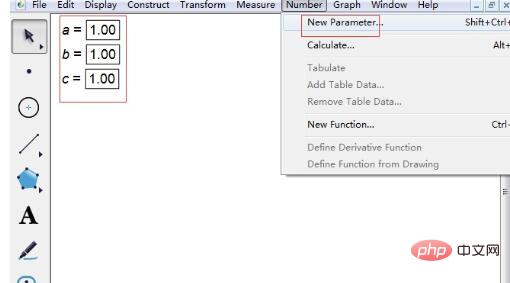
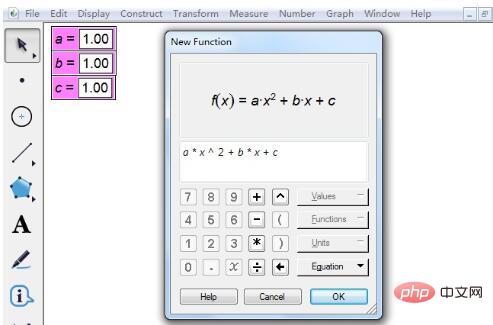
Step 2 Enter the function expression of the quadratic equation. Click [Draw] on the upper menu, select the draw new function option, and enter the expression in the pop-up dialog box. There are a few points to note when entering expressions. 1. When entering parameter a, click the parameter a in the upper left corner with the mouse to enter. Then click the multiplication sign * to enter x. The same goes for other parameters.
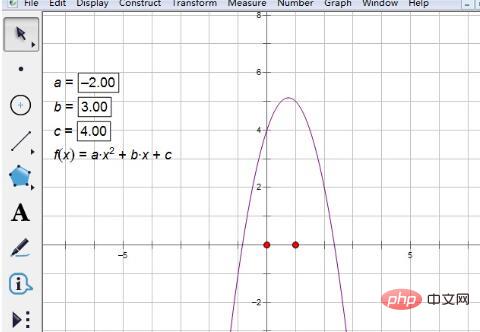
Step 3 Change parameter values. After entering the expression, click [OK] to draw a graph as shown below. Obviously, it has no intersection with the horizontal axis, and the corresponding quadratic equation has no real roots. So to change the value of the parameter, double-click parameter a, and a small window will pop up. Just enter the specific value. The same goes for other parameters.
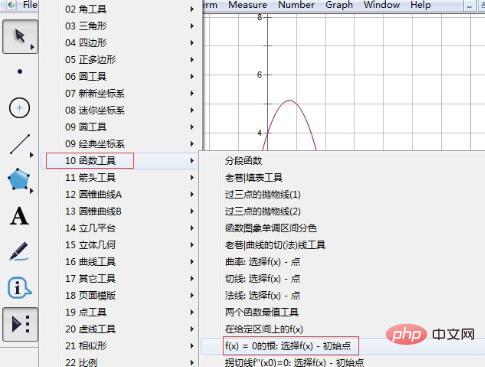
Step 4 Select the function tool. Click the [Custom Tool] button on the left toolbar, and select [Function Tool] from the pop-up shortcut option - the root of f(x)=0.
Step 5 Find the roots of the equation. Click the function analysis expression once, move the cursor, and the root label appears, and one root is displayed. Click the expression again, move the cursor, another root label appears, and the second root is displayed.
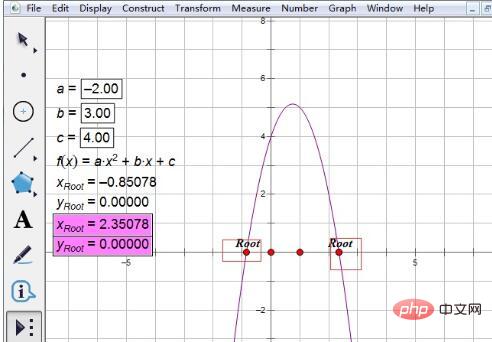
Tips: In this way, the two real roots of the quadratic equation have been found. Note that the two x values are the roots, and y is the ordinate. So how to find the roots of a quadratic equation with arbitrary coefficients? The method is very simple. You just need to double-click the parameters, change the values of a, b, and c, and the roots of the new equation will be displayed immediately.
The above is the detailed content of Detailed method for finding the roots of a quadratic equation using Geometry Sketchpad. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 how to unlink rockstar account from steam
Mar 11, 2025 pm 07:39 PM
how to unlink rockstar account from steam
Mar 11, 2025 pm 07:39 PM
This article explains how to unlink a Rockstar Games Social Club account from Steam. The process involves using the Rockstar Games Launcher to manage linked accounts, removing the Steam connection without impacting game progress or future Steam purc
![[PROVEN] Steam Error e87 Fix: Get Gaming Again in Minutes!](https://img.php.cn/upload/article/202503/18/2025031817560457401.jpg?x-oss-process=image/resize,m_fill,h_207,w_330) [PROVEN] Steam Error e87 Fix: Get Gaming Again in Minutes!
Mar 18, 2025 pm 05:56 PM
[PROVEN] Steam Error e87 Fix: Get Gaming Again in Minutes!
Mar 18, 2025 pm 05:56 PM
Article discusses causes of Steam Error e87, including network issues, security software, server problems, outdated clients, and corrupted files. Offers prevention and solution strategies.[159 characters]
 why is steam downloading so slow
Mar 11, 2025 pm 07:36 PM
why is steam downloading so slow
Mar 11, 2025 pm 07:36 PM
Slow Steam downloads stem from various factors: network congestion (home or ISP), Steam/game server issues, limited bandwidth, high latency, and computer hardware limitations. Troubleshooting involves checking internet speed, optimizing Steam settin
 Steam Error e87: What It Is & How to Fix It
Mar 18, 2025 pm 05:51 PM
Steam Error e87: What It Is & How to Fix It
Mar 18, 2025 pm 05:51 PM
Steam Error e87 occurs during Steam client updates or launches due to connection issues. Fix it by restarting devices, checking server status, changing DNS, disabling security software, clearing cache, or reinstalling Steam.
 Easy Fix: Steam Error e87 Explained & Solved
Mar 18, 2025 pm 05:53 PM
Easy Fix: Steam Error e87 Explained & Solved
Mar 18, 2025 pm 05:53 PM
Steam Error e87, caused by connectivity issues, can be fixed without reinstalling by restarting, checking internet, and clearing cache. Adjusting Steam settings helps prevent future occurrences.
 Steam Error e87: Why It Happens & 5 Ways to Fix It
Mar 18, 2025 pm 05:55 PM
Steam Error e87: Why It Happens & 5 Ways to Fix It
Mar 18, 2025 pm 05:55 PM
Steam Error e87 disrupts gaming on Steam due to connectivity issues. The article discusses causes like unstable internet and server overload, and offers fixes like restarting Steam and checking for updates.
 how to add page numbers in google docs
Mar 14, 2025 pm 02:57 PM
how to add page numbers in google docs
Mar 14, 2025 pm 02:57 PM
The article details how to add, customize, start from a specific page, and remove page numbers in Google Docs using step-by-step instructions.
 How to Fix Steam Error Code e87: The ULTIMATE Guide
Mar 18, 2025 pm 05:51 PM
How to Fix Steam Error Code e87: The ULTIMATE Guide
Mar 18, 2025 pm 05:51 PM
Article discusses fixing Steam Error Code e87, caused by network issues, corrupt files, or client problems. Provides troubleshooting steps and prevention tips.





