Figure 3. Model architecture The overall architecture of QIREN is shown in Figure 3. Consists of N mixed layers and linear layers at the end. The model takes coordinates as input and outputs signal values. The data initially enters the mixed layer, starting with the Linear layer and the BatchNorm layer, resulting in: and is then fed into the data re-upload quantum circuit QC. In Figure 2 (b) and (c), we give the specific implementation of the parameter layer and coding layer quantum circuits. The parameter layer consists of K stacked blocks. Each block contains a spin gate applied to each qubit, as well as CNOT gates connected in a round-robin fashion. The coding layer applies gates on each qubit. Finally, we measure the expected value of a quantum state relative to an observable. The output of a quantum circuit is given by: 
where O represents any observable. The output of the nth blending layer will be used as the input of the (n+1)th layer. Finally, we add a linear layer to receive and output. We use mean square error (MSE) as the loss function to train the model: 
Model theoretical analysisIn some previous studies, the mathematical properties of the data re-upload quantum circuit have been revealed. In essence, the data re-upload quantum circuit is to fit the objective function in the form of a Fourier series. However, previous work only explored multi-layer single-qubit circuits or single-layer multi-qubit circuits, and did not compare with classical methods and did not find the advantages of data re-uploading quantum circuits. We extend our research to multi-layer multi-qubit circuits. In addition, we have proven that in the field of implicit neural representation, the hybrid quantum neural network QIREN, which uses data reuploading quantum circuits as its core component, has exponential advantages over classical methods. We analyzed the role of the quantum layer and the classical layer in QIREN and summarized it into the following three points: 1. Under optimal conditions, the ability of data re-uploading quantum circuits to represent Fourier series increases with the circuit's The size grows exponentially. See sections 4.2 and 4.3 of the paper for specific derivation. 2. The function of the linear layer is to further expand the spectrum and adjust the frequency, thereby improving the fitting performance. Applying a linear layer before uploading data to a quantum circuit is equivalent to adjusting the eigenvalues of the coding layer Hamiltonian, ultimately affecting the spectrum. This approach has two advantages. First, it can make the spectrum larger. Some redundant terms are produced in the spectrum when encoding only with gates. This redundancy can be reduced by using linear layers. Second, it enables the coverage of the spectrum to be adjusted, aiming to cover frequencies with larger coefficients that are more important. Therefore, adding a linear layer can further improve the fitting performance of QIREN. 3. The role of the Batchnorm layer is to accelerate the convergence of the quantum model. In feedforward neural networks, data usually passes through the BatchNorm layer before the activation function, which effectively prevents the vanishing gradient problem. Similarly, in QIREN, quantum circuits replace the activation function and play a role in providing nonlinearity (the quantum circuit itself is linear, but the process of uploading classical data to the quantum circuit is nonlinear). Therefore, we added a BatchNorm layer here with the purpose of stabilizing and accelerating the convergence of the model. We verified QIREN’s superior performance in representing signals, especially high-frequency signals, through image representation and sound representation tasks. The experimental results are shown in Table 1. QIREN and SIREN showed similar performance on the sound representation task. Although the performance of the two models seems to be comparable, it is worth emphasizing that our model achieves 35.1% memory savings with the fewest parameters, and the convergence of SIREN requires setting appropriate hyperparameters, while our model does not This kind of restriction. We then analyzed the model output from a frequency perspective. We visualize the spectrum of the model output in Figure 4 . It is obvious that the low-frequency distributions output by the model are close to the real situation. However, when it comes to high-frequency distributions, both QIREN and SIREN fit well, followed by ReLU-based MLP with random Fourier features (RFF). ReLU-based and Tanh-based MLPs even lack the high-frequency part of the signal.
Table 1. MSE() of the model on signal representation and image super-resolution tasks. Models considered SOTA are marked *. params represents the amount of model parameters, and mem represents the memory saved by the model compared with discrete grid representation.任 Figure 4. Sound indicating the spectrum of the model output in the task. Qiren achieves the best performance in the image representation task. Compared with the SOTA model, the error is The maximum reduction was 34.8%. To further explore the signal representation capabilities of the model, we use filters to separate the high-frequency and low-frequency components of its output and compare the fitting errors of these two components respectively, with the results shown in Figure 5. QIREN consistently achieves the lowest errors when fitting high- and low-frequency components. Figure 5. Relative error of each model compared to Tanh-based MLP. Shaded areas represent low-frequency errors, while unshaded areas represent high-frequency errors. Latest research introduces a breakthrough framework to extend implicit neural representations to image generation. More specifically, the framework utilizes a hypernetwork taking random distributions as input to generate parameters that implicitly characterize the network. Subsequently, these generated parameters are assigned to the implicit representation network. Finally, the implicit representation network generates images taking coordinates as input. An adversarial approach is employed to ensure that the generated images are consistent with our desired results. In this task, we adopt such a framework and build on StyleGAN2. The experimental results are shown in Table 2. We also further explore some exciting features of the QIREN generator, as shown in Figures 6 and 7. F Table 2. FID score of the model on FFHQ and CELEBA-HQ datasets.
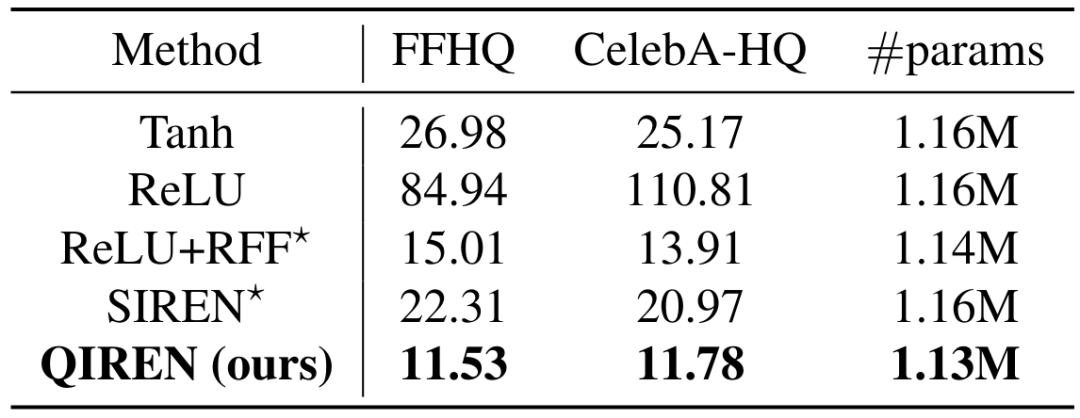
Figure 7. Meaningful image space interpolation 
This work not only integrates quantum advantages into implicit neural representation, but also opens up a promising application direction for quantum neural networks - implicit neural representation. It is worth emphasizing that implicit neural representations have many other potential applications, such as representing scenes or 3D objects, time series prediction, and solving differential equations. For a large class of tasks that model continuous signals, we can consider introducing implicit representation networks as a basic component. Based on the theoretical and experimental foundations of this paper, we can extend QIREN to these applications in future work, and QIREN is expected to produce better results with fewer parameters in these fields. At the same time, we found a suitable application scenario for quantum machine learning. Thereby promoting further practical and innovative research within the quantum machine learning community. 
![[Web front-end] Node.js quick start](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
