DeepMind develops neural network variational Monte Carlo for quantum chemical calculations

Editor | However, quantum chemical calculations of the ground state properties of positron-molecule complexes are challenging.

Here, researchers from DeepMind and Imperial College London tackle this problem using a recently developed Fermionic Neural Network (FermiNet) wave function that does not rely on a basis set. FermiNet was found to produce highly precise, and in some cases state-of-the-art, ground state energies in a range of atoms and small molecules with a variety of qualitative positron binding properties.

The researchers calculated the binding energies of the challenging non-polar benzene molecule and found good agreement with experimental values ​​and obtained annihilation rates that were more favorable than those obtained using explicitly correlated Gaussian wave functions. The results demonstrate the general advantages of methods based on neural network wave functions and apply them to systems other than the standard molecular Hamiltonian.

Relevant research was titled "Neural network variational Monte Carlo for positronic chemistry" and was published in "Nature Communications" on June 18.

Paper link: https://www.nature.com/articles/s41467-024-49290-1 Advances in experimental setups to capture large numbers of positrons have driven the development of more efficient computational tools to describe positron binding state, accelerating the innovation of antimatter technology. Quantum chemical calculations of the ground state properties of positron-molecule complexes are challenging. The main difficulty lies in using an appropriate basis set to represent the coalescence between electrons and positrons.

Although positrons annihilate when in contact with electrons, they can easily form bound states with ordinary molecules. There are many standard tools in computational chemistry that have performed theoretical calculations of positron binding energies and annihilation rates. But describing the positron wave function remains challenging for a number of reasons.
Here, researchers propose a new method for calculating the ground state properties of a molecule's positron-bound state, based on the neural network wave function assumption recently developed for QMC. Fermion neural networks (FermiNet) model multi-body wave functions without reference to a set of basis functions. This conveniently circumvents many of the difficulties described above in describing the positron wave function.
Researchers extended FermiNet to represent the positron component of the wave function equally well as the electron component. Flexible and accurate hybrid electron-positron wave function assumptions can be obtained with minimal changes to the neural network architecture. Positron binding energies and annihilation rates were calculated for a series of systems with different positron binding mechanisms, and the highest accuracy was obtained for the ground state energies of these systems.
Results on positronic hydrides, sodium and magnesium atoms, and small diatomic molecules show that the method can achieve state-of-the-art accuracy compared to previous studies. Furthermore, results for nonpolar dilithium and benzene molecules show that this precision is preserved when describing positron binding modes that are entirely controlled by strong electron-positron correlation effects.
The diagram below provides an intuitive understanding of the binding mechanism between non-polar molecules and positrons: Correlation-dominated binding is facilitated by centers of increased electron density away from the molecule's nuclei. In dilithium this is a covalent bond; in benzene this is an increase in electron density at the center of the molecule due to delocalization of π bonds in the ring.

Illustration: Ground state single particle density of positron lithium and benzene. (Source: paper) The positron binding energy of benzene obtained by this method is very close to the experimental value and the many-body theory of Hofierka et al. at Queen's University. And the obtained annihilation rates are comparable to high-precision ECG-SVM calculations of alkali metal atoms and small molecules. Furthermore, the 2γ annihilation rates of positron atoms and molecules accumulated using the FermiNet wave function are compared with the results obtained by various other calculation methods, as shown in the following table: Table: Compared with the annihilation rates obtained by various other calculation methods Ratio, 2γ annihilation rates of positron atoms and molecules accumulated using FermiNet wave functions. (Source: paper)

1. Compared with other methods, ECG-SVM calculates the annihilation rate by constructing features that best capture the wave function.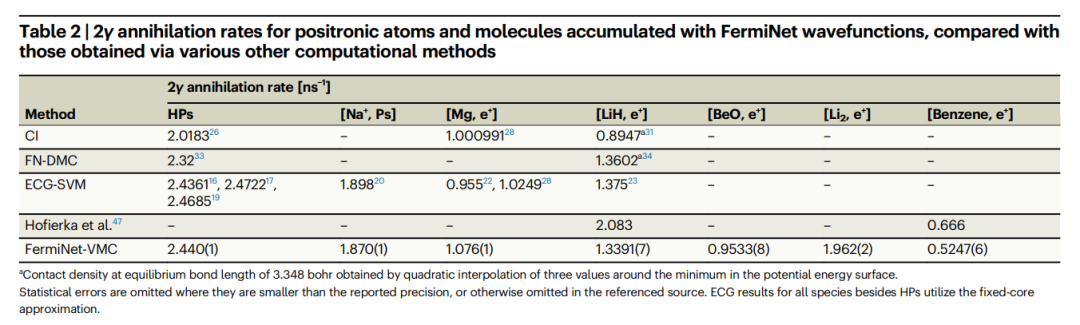

2. The study found that for positron hydride, lithium hydride and alkali metal atoms, the annihilation rate results of FermiNet-VMC and ECG-SVM are very consistent.

This shows that FermiNet-VMC provides an accurate description of electron-positron correlations and is more suitable for calculating annihilation rates than the many-body theory results of Hofierka et al.

3. In summary, the ECG-SVM method produces highly accurate results for a wide variety of molecules with various positron binding mechanisms without system-specific adjustments.

The above is the detailed content of DeepMind develops neural network variational Monte Carlo for quantum chemical calculations. For more information, please follow other related articles on the PHP Chinese website!