
This section analyzes and designs an efficient algorithm for finding Fibonacci numbers using dynamic programming. Section 18.3, Case Study: Computing Fibonacci Numbers, gave a recursive method for finding the Fibonacci number, as follows:
/**The method for finding the Fibonacci number*/
public static long fib(long index) {
if (index == 0) // Base case
return 0;
else if (index == 1) // Base case
return 1;
else // Reduction and recursive calls
return fib(index - 1) + fib(index - 2);
}
We can now prove that the complexity of this algorithm is O(2^n). For convenience, let the index be n. Let T(n) denote the complexity for the algorithm that finds fib(n) and c denote the constant time for comparing the index with 0 and 1; that is, T(1) and T(0) are c. Thus,

Similar to the analysis of the Tower of Hanoi problem, we can show that T(n) is O(2^n).
However, this algorithm is not efficient. Is there an efficient algorithm for finding a Fibonacci number? The trouble with the recursive fib method is that the method is invoked redundantly with the same arguments. For example, to compute fib(4), fib(3) and fib(2) are invoked. To compute fib(3), fib(2) and fib(1) are invoked. Note that fib(2) is redundantly invoked. We can improve it by avoiding repeatedly calling of the fib method with the same argument. Note that a new Fibonacci number is obtained by adding the preceding two numbers in the sequence. If you use the two variables f0 and f1 to store the two preceding numbers, the new number, f2, can be immediately obtained by adding f0 with f1. Now you should update f0 and f1 by assigning f1 to f0 and assigning f2 to f1, as shown in Figure below.

The new method is implemented in the code below.
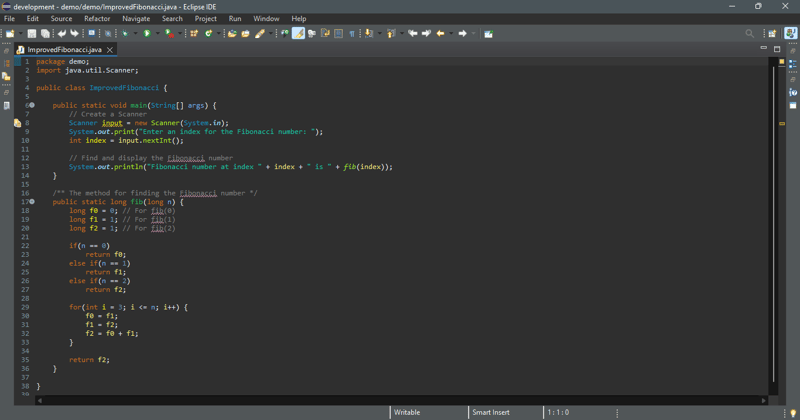
Enter an index for the Fibonacci number: 6
Fibonacci number at index 6 is 8
Enter an index for the Fibonacci number: 7
Fibonacci number at index 7 is 13
Obviously, the complexity of this new algorithm is O(n). This is a tremendous improvement over the recursive O(2^n) algorithm.
The algorithm for computing Fibonacci numbers presented here uses an approach known as dynamic programming. Dynamic programming is the process of solving subproblems, then combining the solutions of the subproblems to obtain an overall solution. This naturally leads to a recursive solution. However, it would be inefficient to use recursion, because the subproblems overlap. The key idea behind dynamic programming is to solve each subproblem only once and store the results for subproblems for later use to avoid redundant computing of the subproblems.
The above is the detailed content of Finding Fibonacci Numbers Using Dynamic Programming. For more information, please follow other related articles on the PHP Chinese website!




