 Technology peripherals
Technology peripherals
 AI
AI
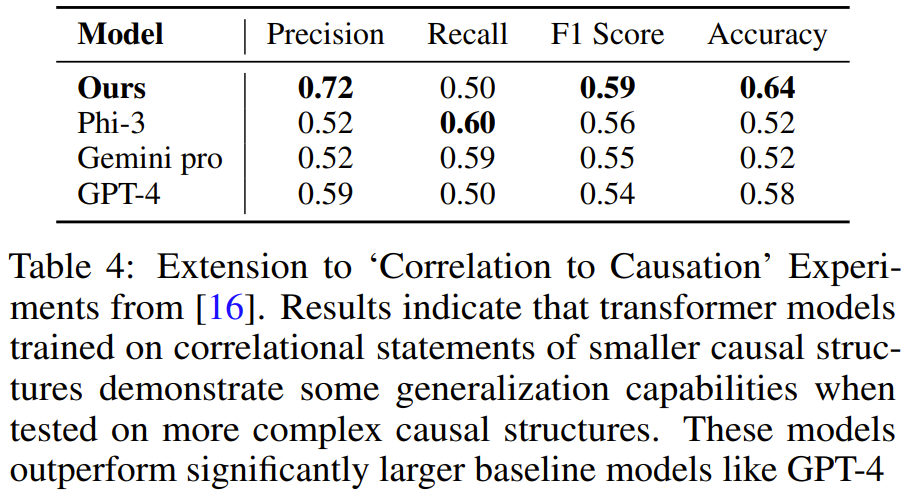
 Axiomatic training allows LLM to learn causal reasoning: the 67 million parameter model is comparable to the trillion parameter level GPT-4
Axiomatic training allows LLM to learn causal reasoning: the 67 million parameter model is comparable to the trillion parameter level GPT-4
Axiomatic training allows LLM to learn causal reasoning: the 67 million parameter model is comparable to the trillion parameter level GPT-4
Show the causal chain to LLM and it will learn the axioms.

Paper title: Teaching Transformers Causal Reasoning through Axiomatic Training Paper address: https://arxiv.org/pdf/2407.07612
 , and the conclusion is "yes".
, and the conclusion is "yes".  , where n is the number of nodes in each i-th premise. P is the premise, that is, a natural language expression of a certain causal structure (such as X causes Y, Y causes Z); followed by the question H (such as does X cause Y?); L is the label (Yes or No). This form effectively covers all pairs of nodes for each unique chain in a given causal graph.
, where n is the number of nodes in each i-th premise. P is the premise, that is, a natural language expression of a certain causal structure (such as X causes Y, Y causes Z); followed by the question H (such as does X cause Y?); L is the label (Yes or No). This form effectively covers all pairs of nodes for each unique chain in a given causal graph.  The analysis shows that compared to the next token prediction, using this Losses can yield promising results.
The analysis shows that compared to the next token prediction, using this Losses can yield promising results. 




The above is the detailed content of Axiomatic training allows LLM to learn causal reasoning: the 67 million parameter model is comparable to the trillion parameter level GPT-4. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1664
1664
 14
14
 1422
1422
 52
52
 1316
1316
 25
25
 1266
1266
 29
29
 1239
1239
 24
24
 The author of ControlNet has another hit! The whole process of generating a painting from a picture, earning 1.4k stars in two days
Jul 17, 2024 am 01:56 AM
The author of ControlNet has another hit! The whole process of generating a painting from a picture, earning 1.4k stars in two days
Jul 17, 2024 am 01:56 AM
It is also a Tusheng video, but PaintsUndo has taken a different route. ControlNet author LvminZhang started to live again! This time I aim at the field of painting. The new project PaintsUndo has received 1.4kstar (still rising crazily) not long after it was launched. Project address: https://github.com/lllyasviel/Paints-UNDO Through this project, the user inputs a static image, and PaintsUndo can automatically help you generate a video of the entire painting process, from line draft to finished product. follow. During the drawing process, the line changes are amazing. The final video result is very similar to the original image: Let’s take a look at a complete drawing.
 Topping the list of open source AI software engineers, UIUC's agent-less solution easily solves SWE-bench real programming problems
Jul 17, 2024 pm 10:02 PM
Topping the list of open source AI software engineers, UIUC's agent-less solution easily solves SWE-bench real programming problems
Jul 17, 2024 pm 10:02 PM
The AIxiv column is a column where this site publishes academic and technical content. In the past few years, the AIxiv column of this site has received more than 2,000 reports, covering top laboratories from major universities and companies around the world, effectively promoting academic exchanges and dissemination. If you have excellent work that you want to share, please feel free to contribute or contact us for reporting. Submission email: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com The authors of this paper are all from the team of teacher Zhang Lingming at the University of Illinois at Urbana-Champaign (UIUC), including: Steven Code repair; Deng Yinlin, fourth-year doctoral student, researcher
 From RLHF to DPO to TDPO, large model alignment algorithms are already 'token-level'
Jun 24, 2024 pm 03:04 PM
From RLHF to DPO to TDPO, large model alignment algorithms are already 'token-level'
Jun 24, 2024 pm 03:04 PM
The AIxiv column is a column where this site publishes academic and technical content. In the past few years, the AIxiv column of this site has received more than 2,000 reports, covering top laboratories from major universities and companies around the world, effectively promoting academic exchanges and dissemination. If you have excellent work that you want to share, please feel free to contribute or contact us for reporting. Submission email: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com In the development process of artificial intelligence, the control and guidance of large language models (LLM) has always been one of the core challenges, aiming to ensure that these models are both powerful and safe serve human society. Early efforts focused on reinforcement learning methods through human feedback (RL
 arXiv papers can be posted as 'barrage', Stanford alphaXiv discussion platform is online, LeCun likes it
Aug 01, 2024 pm 05:18 PM
arXiv papers can be posted as 'barrage', Stanford alphaXiv discussion platform is online, LeCun likes it
Aug 01, 2024 pm 05:18 PM
cheers! What is it like when a paper discussion is down to words? Recently, students at Stanford University created alphaXiv, an open discussion forum for arXiv papers that allows questions and comments to be posted directly on any arXiv paper. Website link: https://alphaxiv.org/ In fact, there is no need to visit this website specifically. Just change arXiv in any URL to alphaXiv to directly open the corresponding paper on the alphaXiv forum: you can accurately locate the paragraphs in the paper, Sentence: In the discussion area on the right, users can post questions to ask the author about the ideas and details of the paper. For example, they can also comment on the content of the paper, such as: "Given to
 Posthumous work of the OpenAI Super Alignment Team: Two large models play a game, and the output becomes more understandable
Jul 19, 2024 am 01:29 AM
Posthumous work of the OpenAI Super Alignment Team: Two large models play a game, and the output becomes more understandable
Jul 19, 2024 am 01:29 AM
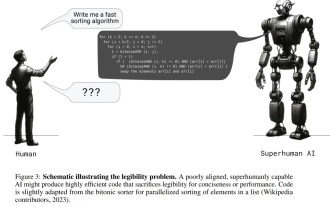
If the answer given by the AI model is incomprehensible at all, would you dare to use it? As machine learning systems are used in more important areas, it becomes increasingly important to demonstrate why we can trust their output, and when not to trust them. One possible way to gain trust in the output of a complex system is to require the system to produce an interpretation of its output that is readable to a human or another trusted system, that is, fully understandable to the point that any possible errors can be found. For example, to build trust in the judicial system, we require courts to provide clear and readable written opinions that explain and support their decisions. For large language models, we can also adopt a similar approach. However, when taking this approach, ensure that the language model generates
 A significant breakthrough in the Riemann Hypothesis! Tao Zhexuan strongly recommends new papers from MIT and Oxford, and the 37-year-old Fields Medal winner participated
Aug 05, 2024 pm 03:32 PM
A significant breakthrough in the Riemann Hypothesis! Tao Zhexuan strongly recommends new papers from MIT and Oxford, and the 37-year-old Fields Medal winner participated
Aug 05, 2024 pm 03:32 PM
Recently, the Riemann Hypothesis, known as one of the seven major problems of the millennium, has achieved a new breakthrough. The Riemann Hypothesis is a very important unsolved problem in mathematics, related to the precise properties of the distribution of prime numbers (primes are those numbers that are only divisible by 1 and themselves, and they play a fundamental role in number theory). In today's mathematical literature, there are more than a thousand mathematical propositions based on the establishment of the Riemann Hypothesis (or its generalized form). In other words, once the Riemann Hypothesis and its generalized form are proven, these more than a thousand propositions will be established as theorems, which will have a profound impact on the field of mathematics; and if the Riemann Hypothesis is proven wrong, then among these propositions part of it will also lose its effectiveness. New breakthrough comes from MIT mathematics professor Larry Guth and Oxford University
 The first Mamba-based MLLM is here! Model weights, training code, etc. have all been open source
Jul 17, 2024 am 02:46 AM
The first Mamba-based MLLM is here! Model weights, training code, etc. have all been open source
Jul 17, 2024 am 02:46 AM
The AIxiv column is a column where this site publishes academic and technical content. In the past few years, the AIxiv column of this site has received more than 2,000 reports, covering top laboratories from major universities and companies around the world, effectively promoting academic exchanges and dissemination. If you have excellent work that you want to share, please feel free to contribute or contact us for reporting. Submission email: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com. Introduction In recent years, the application of multimodal large language models (MLLM) in various fields has achieved remarkable success. However, as the basic model for many downstream tasks, current MLLM consists of the well-known Transformer network, which
 LLM is really not good for time series prediction. It doesn't even use its reasoning ability.
Jul 15, 2024 pm 03:59 PM
LLM is really not good for time series prediction. It doesn't even use its reasoning ability.
Jul 15, 2024 pm 03:59 PM
Can language models really be used for time series prediction? According to Betteridge's Law of Headlines (any news headline ending with a question mark can be answered with "no"), the answer should be no. The fact seems to be true: such a powerful LLM cannot handle time series data well. Time series, that is, time series, as the name suggests, refers to a set of data point sequences arranged in the order of time. Time series analysis is critical in many areas, including disease spread prediction, retail analytics, healthcare, and finance. In the field of time series analysis, many researchers have recently been studying how to use large language models (LLM) to classify, predict, and detect anomalies in time series. These papers assume that language models that are good at handling sequential dependencies in text can also generalize to time series.



