The AIxiv column is a column where this site publishes academic and technical content. In the past few years, the AIxiv column of this site has received more than 2,000 reports, covering top laboratories from major universities and companies around the world, effectively promoting academic exchanges and dissemination. If you have excellent work that you want to share, please feel free to contribute or contact us for reporting. Submission email: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com
This work was completed by the team of IEEE Fellow Chen Enhong of the National Key Laboratory of Cognitive Intelligence at the University of Science and Technology of China and Huawei's Noah's Ark Laboratory. Professor Chen Enhong’s team is deeply engaged in the fields of data mining and machine learning, and has published many papers in top journals and conferences. Google Scholar papers have been cited more than 20,000 times. Noah's Ark Laboratory is Huawei's laboratory engaged in basic research on artificial intelligence. It adheres to the concept of equal emphasis on theoretical research and application innovation, and is committed to promoting technological innovation and development in the field of artificial intelligence. Data is the cornerstone of the success of large language models (LLMs), but not all data is beneficial to model learning. Intuitively, high-quality samples are expected to have better efficiency in teaching LLM. Therefore, existing methods usually focus on quality-based data selection. However, most of these methods evaluate different data samples independently, ignoring the complex combinatorial effects between samples. As shown in Figure 1, even if each sample is of perfect quality, their combination may still be suboptimal due to their mutual information redundancy or inconsistency. Although the quality-based subset consists of all three quality samples, the knowledge they encode is actually redundant and conflicting. In contrast, another data subset consisting of several relatively lower quality but diverse samples may be more informative in teaching LLM. Therefore, quality-based data selection is not fully aligned with the goal of maximizing LLM knowledge capture. And this article aims to reveal the intrinsic relationship between LLM performance and data selection. Inspired by the nature of LLM information compression, we discovered an entropy law, which links LLM performance to the data compression rate and the loss of previous steps of model training, which respectively reflects the degree of information redundancy of the data set and the inherent effect of LLM on the data set. The degree of knowledge mastery. Through theoretical derivation and empirical evaluation, we find that model performance is inversely related to the compression ratio of training data, which usually results in lower training loss. Based on the findings of entropy law, we propose a very efficient and general data selection method for training LLM, named ZIP, which aims to preferentially select low compression ratio data subsets. ZIP greedily selects diverse data in multiple stages, ultimately obtaining a data subset with good diversity. 
- Team: Chen Enhong’s team at National Key Laboratory of Cognitive Intelligence, University of Science and Technology of China, Huawei Noah’s Ark Laboratory
- Paper link: https://arxiv.org/pdf/2407.06645
- Code link : https://github.com/USTC-StarTeam/ZIP

O Figure 1 tENTropy Law
We analyze the theoretical analysis of the relationship between data compression and LLM performance. Intuitively, the correctness and diversity of training data will affect the performance of the final model. At the same time, LLM performance may be suboptimal if the data has severe inherent conflicts or if the model has a poor grasp of the information encoded in the data. Based on these assumptions, we denote the performance of LLM as Z , which is expected to be affected by:
Data compression ratio R: Intuitively, datasets with lower compression ratios indicate higher information density.
Training loss L: Indicates whether the data is difficult for the model to remember. Under the same base model, high training loss is usually due to the presence of noise or inconsistent information in the data set.
- Data consistency C: The consistency of data is reflected by the entropy of the probability of the next token given the previous situation. Higher data consistency usually leads to lower training loss.
- Average data quality Q: reflects the average sample-level quality of the data, which can be measured through various objective and subjective aspects.
- Given a certain amount of training data, model performance can be estimated by the above factors:
where f is an implicit function. Given a specific base model, the scale of L usually depends on R and C and can be expressed as:
Since a dataset with higher homogeneity or better data consistency is easier to be learned by the model, L It is expected to be monotonic in R and C. Therefore, we can rewrite the above formula as: 
where g' is an inverse function. By combining the above three equations, we get: 
where h is another implicit function. If the data selection method does not significantly change the average data quality Q, we can approximately treat the variable Q as a constant. Therefore, the final performance can be roughly expressed as:  This means that the model performance is related to the data compression rate and training loss. We call this relationship Entropy law. Based on Entropy law, we propose two inferences:
This means that the model performance is related to the data compression rate and training loss. We call this relationship Entropy law. Based on Entropy law, we propose two inferences:
- If C is regarded as a constant, the training loss is directly affected by the compression rate. Therefore, model performance is controlled by the compression ratio: if the data compression ratio R is higher, then Z is usually worse, which will be verified in our experiments.
- Under the same compression ratio, higher training loss means lower data consistency. Therefore, the effective knowledge learned by the model may be more limited. This can be used to predict the performance of LLM on different data with similar compression ratio and sample quality. We will show the application of this reasoning in practice later.
ZIP: Highly lightweight data selection algorithm Under the guidance of entropy law, we proposed ZIP, a data selection method, to select data samples through data compression rate, aiming to Maximize the amount of effective information under limited training data budget. For efficiency reasons, we adopt an iterative multi-stage greedy paradigm to efficiently obtain approximate solutions with relatively low compression rates. In each iteration, we first use a global selection stage to select a pool of candidate samples with low compression ratio to find samples with high information density. We then employ a coarse-grained local selection stage to select a set of smaller samples that have the lowest redundancy with the selected samples. Finally, we use a fine-grained local selection stage to minimize the similarity between the samples to be added. The above process continues until sufficient data is obtained. The specific algorithm is as follows: 
1. Effectiveness of the ZIP selection algorithm for different LLMs and in different LLM alignment stagesComparing different SFT data selection algorithms, the model trained based on ZIP selection data shows advantages in performance and is also superior in efficiency. The specific results are shown in the table below: 
Thanks to the model-independent and content-insensitive characteristics of ZIP, it can also be applied to data selection in the preference alignment stage. The data selected by ZIP also shows great advantages. The specific results are shown in the table below: 
2. Experimental verification of Entropy lawBased on the SFT data selection experiment, we based on the model effect, data compression rate and the loss of the model in the previous steps of training, respectively Multiple relationship curves were fitted. The results are shown in Figures 2 and 3, from which we can observe the close correlation between the three factors. First of all, low compression rate data usually leads to better model results. This is because the learning process of LLMs is highly related to information compression. We can think of LLM as a data compressor, so data with lower compression rate means more amount of knowledge and thus more valuable to the compressor. At the same time, it can be observed that lower compression ratios are usually accompanied by higher training losses. This is because data that is difficult to compress carries more knowledge, posing greater challenges for LLM to absorb the knowledge contained in it. 
The above is the detailed content of The University of Science and Technology of China and Huawei Noah proposed Entropy Law to reveal the relationship between large model performance, data compression rate and training loss.. For more information, please follow other related articles on the PHP Chinese website!






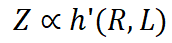




 到
到 是逐渐增量更新的 5 个数据版本,出于保密要求,仅提供不同压缩率下模型效果的相对关系。根据 entropy law 预测,假设每次增量更新后数据质量没有显着下降,可以预期随着数据压缩率的降低,模型性能会有所提升。这一预测与图中数据版本
是逐渐增量更新的 5 个数据版本,出于保密要求,仅提供不同压缩率下模型效果的相对关系。根据 entropy law 预测,假设每次增量更新后数据质量没有显着下降,可以预期随着数据压缩率的降低,模型性能会有所提升。这一预测与图中数据版本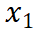 到
到 的结果一致。然而,数据版本
的结果一致。然而,数据版本 显示出损失和数据压缩率的异常增加,这预示了由于训练数据一致性下降导致的模型性能下降的潜在可能。这一预测通过随后的模型性能评估进一步得到证实。因此,entropy law 可以作为 LLM 训练的指导原则,无需在完整数据集上训练模型直到收敛,便可预测 LLM 训练失败的潜在风险。鉴于训练 LLM 的高昂成本,这一点尤其重要。
显示出损失和数据压缩率的异常增加,这预示了由于训练数据一致性下降导致的模型性能下降的潜在可能。这一预测通过随后的模型性能评估进一步得到证实。因此,entropy law 可以作为 LLM 训练的指导原则,无需在完整数据集上训练模型直到收敛,便可预测 LLM 训练失败的潜在风险。鉴于训练 LLM 的高昂成本,这一点尤其重要。 




