 Technology peripherals
Technology peripherals
 AI
AI
 Progress was made for the first time in decades, apprentices Tao Zhexuan and Zhao Yufei broke through combinatorial mathematics problems
Progress was made for the first time in decades, apprentices Tao Zhexuan and Zhao Yufei broke through combinatorial mathematics problems
Progress was made for the first time in decades, apprentices Tao Zhexuan and Zhao Yufei broke through combinatorial mathematics problems
Recently, for the first time, progress has been made on a decades-old unsolved mathematical problem.
Driving this progress are UCLA graduate student James Leng and MIT mathematics graduate student Ashwin Sah, and Columbia University assistant professor Mehtaab Sawhney. Among them, James Leng studied under the famous mathematician Terence Tao, and Ashwin Sah studied under the discrete mathematics master Zhao Yufei.

Paper address: https://arxiv.org/pdf/2402.17995
To understand the breakthrough achieved in this research, you need to start with arithmetic progressions.
The sum of the first n terms of an arithmetic sequence is called an arithmetic series, also called an arithmetic series. In 1936, mathematicians Paul Erdős and Pál Turán conjectured that if a set consists of nonzero fractions of integers (even 0.00000001%), then it must contain an arbitrarily long arithmetic series. The only sets that can avoid arithmetic series are those that contain a "negligible" part of the integers. For example, the set {2, 4, 8, 16, …}, where each number is twice the previous number, is spread out along the number axis without progression.
In 1975, mathematician Endre Szemerédi proved this conjecture. His work gave rise to a variety of research directions that mathematicians are still exploring today.
Mathematicians established Szemerédi’s result in the context of a finite set of numbers (all integers from 1 to some number N). How much of the initial pool can be used in the set before inevitably including a forbidden series? How does this proportion change as N changes?
For example, let N be 20, how many of these 20 numbers can be written down while still avoiding series that are 5 or more numbers in length? The answer, it turns out, is 16% to 80% of the initial pool.
Szemerédi was the first to show that as N grows, this fraction must shrink to zero, and mathematicians have since tried to quantify how quickly this happens.
Last year, groundbreaking work by two computer scientists nearly solved the problem of three-term series, such as {6, 11, 16}. But the problem becomes more difficult when you try to avoid arithmetic series of four or more terms. This is because longer series reflect underlying structures that are difficult to reveal using classical mathematical methods.
The numbers x, y and z in the three-term arithmetic series always satisfy the simple equation x – 2y + z = 0 (taking the series {10, 20, 30} as an example: 10 – 2*(20) + 30 = 0), it is relatively easy to prove whether a set contains numbers that satisfy this condition. While the numbers in a four-term series must also satisfy the more complex equation x^2 – 3y^2 + 3z^2 – w^2 = 0, a series with five or more terms must satisfy an even more complex equation. This means that sets containing such series will exhibit more subtle patterns. It would also be harder for mathematicians to prove whether such a pattern exists.
In the late 1990s, mathematician Timothy Gowers proposed a theory to overcome this obstacle. He was later awarded the Fields Medal, mathematics' highest honor, in part for this work. In 2001, he applied his method to Szemerédi's theorem, proving better bounds on the maximum set size, avoiding arithmetic series for any given length.
In 2022, James Leng, then a second-year graduate student at UCLA, began to understand Gowers’ theory. He did not consider Szemerédi's theorem. Instead, he hopes to answer questions about Gowers' approach.
However, after trying hard to explore for more than a year, he found nothing.
Sah and Sawhney, who have been thinking about related issues, learned about Leng’s work and were very interested. Sawhney even said: "I am surprised that I can think like this."
Sah and Sawhney realized that Leng's research might help them make further progress on Szemerédi's theorem. Within a few months, three young mathematicians figured out how to get better upper bounds on the size of sets without pentterm series. They then extended their work to series of arbitrary lengths, marking the first progress on the problem in the 23 years since Gowers' proof.
Let 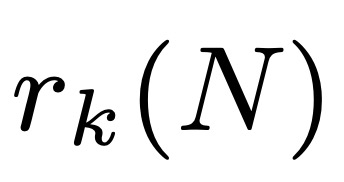 denote
denote  , the size of the largest subset of an arithmetic series without k terms. Leng, Sah and Sawhney showed that for k ≥ 5, there exists c_k > 0 such that
, the size of the largest subset of an arithmetic series without k terms. Leng, Sah and Sawhney showed that for k ≥ 5, there exists c_k > 0 such that 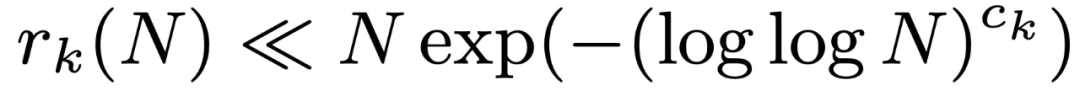 .
.
Research Team
The first author of the paper James Leng is a graduate student in mathematics at the University of California, Los Angeles (UCLA), and received his undergraduate degree from the University of California, Berkeley. He studied under the famous mathematician Terence Tao.
James Leng’s research interests include arithmetic combinatorics, dynamical systems, Fourier analysis, etc. His research has also been supported by an NSF graduate fellowship.

. In the summer of 2016, 16-year-old Sah won the gold medal in the International Mathematics Olympiad (IMO). The following year he entered MIT to study.
 Ashwin Sah
Ashwin Sah
During his studies at MIT, there were two people who played an important role in Sah’s mathematical development. The first one is Professor Yufei Zhao, a master of discrete mathematics, who is also Sah’s graduate tutor. The second one is Mehtaab Sawhney, they met in class and became friends. Later, the two did research together and discussed various topics in the field of discrete mathematics, such as graph theory, probability theory and the properties of random matrices. Ashwin Sah and Mehtaab Sawhney met at the end of 2017 when they were undergraduate students at (MIT). Since then, the two have written an incredible 57 mathematical proofs together, many of which have had profound consequences in various fields.
 Mehtaab Sawhney
Mehtaab Sawhney
Mehtaab Sawhney is currently an assistant professor at Columbia University. His research interests include combinatorics, probability, and theoretical computer science, among others.
Reference link: https://www.quantamagazine.org/grad-students-find-inevitable-patterns-in-big-sets-of-numbers-20240805/
The above is the detailed content of Progress was made for the first time in decades, apprentices Tao Zhexuan and Zhao Yufei broke through combinatorial mathematics problems. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1664
1664
 14
14
 1423
1423
 52
52
 1317
1317
 25
25
 1268
1268
 29
29
 1246
1246
 24
24
 The author of ControlNet has another hit! The whole process of generating a painting from a picture, earning 1.4k stars in two days
Jul 17, 2024 am 01:56 AM
The author of ControlNet has another hit! The whole process of generating a painting from a picture, earning 1.4k stars in two days
Jul 17, 2024 am 01:56 AM
It is also a Tusheng video, but PaintsUndo has taken a different route. ControlNet author LvminZhang started to live again! This time I aim at the field of painting. The new project PaintsUndo has received 1.4kstar (still rising crazily) not long after it was launched. Project address: https://github.com/lllyasviel/Paints-UNDO Through this project, the user inputs a static image, and PaintsUndo can automatically help you generate a video of the entire painting process, from line draft to finished product. follow. During the drawing process, the line changes are amazing. The final video result is very similar to the original image: Let’s take a look at a complete drawing.
 Topping the list of open source AI software engineers, UIUC's agent-less solution easily solves SWE-bench real programming problems
Jul 17, 2024 pm 10:02 PM
Topping the list of open source AI software engineers, UIUC's agent-less solution easily solves SWE-bench real programming problems
Jul 17, 2024 pm 10:02 PM
The AIxiv column is a column where this site publishes academic and technical content. In the past few years, the AIxiv column of this site has received more than 2,000 reports, covering top laboratories from major universities and companies around the world, effectively promoting academic exchanges and dissemination. If you have excellent work that you want to share, please feel free to contribute or contact us for reporting. Submission email: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com The authors of this paper are all from the team of teacher Zhang Lingming at the University of Illinois at Urbana-Champaign (UIUC), including: Steven Code repair; Deng Yinlin, fourth-year doctoral student, researcher
 From RLHF to DPO to TDPO, large model alignment algorithms are already 'token-level'
Jun 24, 2024 pm 03:04 PM
From RLHF to DPO to TDPO, large model alignment algorithms are already 'token-level'
Jun 24, 2024 pm 03:04 PM
The AIxiv column is a column where this site publishes academic and technical content. In the past few years, the AIxiv column of this site has received more than 2,000 reports, covering top laboratories from major universities and companies around the world, effectively promoting academic exchanges and dissemination. If you have excellent work that you want to share, please feel free to contribute or contact us for reporting. Submission email: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com In the development process of artificial intelligence, the control and guidance of large language models (LLM) has always been one of the core challenges, aiming to ensure that these models are both powerful and safe serve human society. Early efforts focused on reinforcement learning methods through human feedback (RL
 arXiv papers can be posted as 'barrage', Stanford alphaXiv discussion platform is online, LeCun likes it
Aug 01, 2024 pm 05:18 PM
arXiv papers can be posted as 'barrage', Stanford alphaXiv discussion platform is online, LeCun likes it
Aug 01, 2024 pm 05:18 PM
cheers! What is it like when a paper discussion is down to words? Recently, students at Stanford University created alphaXiv, an open discussion forum for arXiv papers that allows questions and comments to be posted directly on any arXiv paper. Website link: https://alphaxiv.org/ In fact, there is no need to visit this website specifically. Just change arXiv in any URL to alphaXiv to directly open the corresponding paper on the alphaXiv forum: you can accurately locate the paragraphs in the paper, Sentence: In the discussion area on the right, users can post questions to ask the author about the ideas and details of the paper. For example, they can also comment on the content of the paper, such as: "Given to
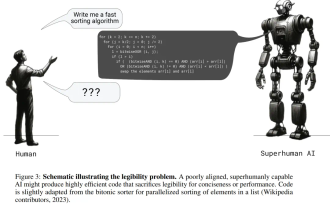 Posthumous work of the OpenAI Super Alignment Team: Two large models play a game, and the output becomes more understandable
Jul 19, 2024 am 01:29 AM
Posthumous work of the OpenAI Super Alignment Team: Two large models play a game, and the output becomes more understandable
Jul 19, 2024 am 01:29 AM
If the answer given by the AI model is incomprehensible at all, would you dare to use it? As machine learning systems are used in more important areas, it becomes increasingly important to demonstrate why we can trust their output, and when not to trust them. One possible way to gain trust in the output of a complex system is to require the system to produce an interpretation of its output that is readable to a human or another trusted system, that is, fully understandable to the point that any possible errors can be found. For example, to build trust in the judicial system, we require courts to provide clear and readable written opinions that explain and support their decisions. For large language models, we can also adopt a similar approach. However, when taking this approach, ensure that the language model generates
 A significant breakthrough in the Riemann Hypothesis! Tao Zhexuan strongly recommends new papers from MIT and Oxford, and the 37-year-old Fields Medal winner participated
Aug 05, 2024 pm 03:32 PM
A significant breakthrough in the Riemann Hypothesis! Tao Zhexuan strongly recommends new papers from MIT and Oxford, and the 37-year-old Fields Medal winner participated
Aug 05, 2024 pm 03:32 PM
Recently, the Riemann Hypothesis, known as one of the seven major problems of the millennium, has achieved a new breakthrough. The Riemann Hypothesis is a very important unsolved problem in mathematics, related to the precise properties of the distribution of prime numbers (primes are those numbers that are only divisible by 1 and themselves, and they play a fundamental role in number theory). In today's mathematical literature, there are more than a thousand mathematical propositions based on the establishment of the Riemann Hypothesis (or its generalized form). In other words, once the Riemann Hypothesis and its generalized form are proven, these more than a thousand propositions will be established as theorems, which will have a profound impact on the field of mathematics; and if the Riemann Hypothesis is proven wrong, then among these propositions part of it will also lose its effectiveness. New breakthrough comes from MIT mathematics professor Larry Guth and Oxford University
 LLM is really not good for time series prediction. It doesn't even use its reasoning ability.
Jul 15, 2024 pm 03:59 PM
LLM is really not good for time series prediction. It doesn't even use its reasoning ability.
Jul 15, 2024 pm 03:59 PM
Can language models really be used for time series prediction? According to Betteridge's Law of Headlines (any news headline ending with a question mark can be answered with "no"), the answer should be no. The fact seems to be true: such a powerful LLM cannot handle time series data well. Time series, that is, time series, as the name suggests, refers to a set of data point sequences arranged in the order of time. Time series analysis is critical in many areas, including disease spread prediction, retail analytics, healthcare, and finance. In the field of time series analysis, many researchers have recently been studying how to use large language models (LLM) to classify, predict, and detect anomalies in time series. These papers assume that language models that are good at handling sequential dependencies in text can also generalize to time series.
 The first Mamba-based MLLM is here! Model weights, training code, etc. have all been open source
Jul 17, 2024 am 02:46 AM
The first Mamba-based MLLM is here! Model weights, training code, etc. have all been open source
Jul 17, 2024 am 02:46 AM
The AIxiv column is a column where this site publishes academic and technical content. In the past few years, the AIxiv column of this site has received more than 2,000 reports, covering top laboratories from major universities and companies around the world, effectively promoting academic exchanges and dissemination. If you have excellent work that you want to share, please feel free to contribute or contact us for reporting. Submission email: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com. Introduction In recent years, the application of multimodal large language models (MLLM) in various fields has achieved remarkable success. However, as the basic model for many downstream tasks, current MLLM consists of the well-known Transformer network, which



