Maximum Number of Points with Cost
1937. Maximum Number of Points with Cost
Difficulty: Medium
Topics: Array, Dynamic Programming
You are given an m x n integer matrix points (0-indexed). Starting with 0 points, you want to maximize the number of points you can get from the matrix.
To gain points, you must pick one cell in each row. Picking the cell at coordinates (r, c) will add points[r][c] to your score.
However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows r and r + 1 (where 0 <= r < m - 1), picking cells at coordinates (r, c1) and (r + 1, c2) will subtract abs(c1 - c2) from your score.
Return the maximum number of points you can achieve.
abs(x) is defined as:
- x for x >= 0.
- -x for x < 0.
Example 1:
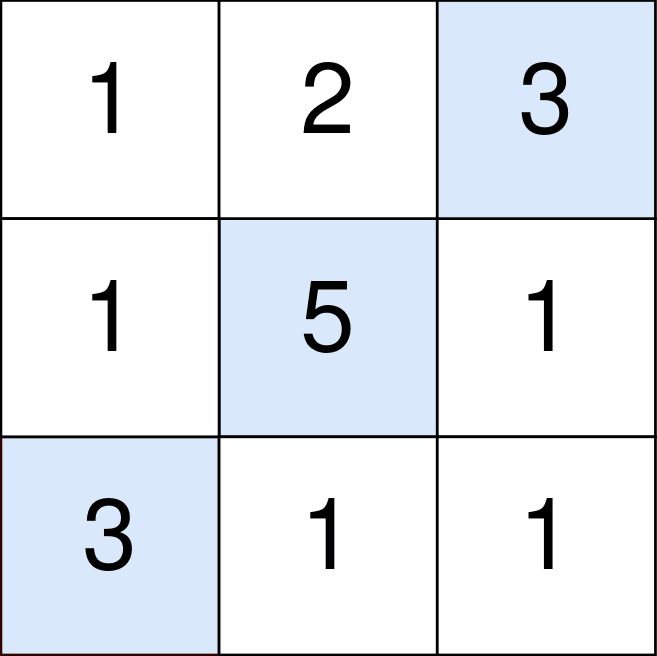
- Input: l1 = [2,4,3], l2 = [5,6,4]
- Output: 9
-
Explanation:
- The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0).
- You add 3 + 5 + 3 = 11 to your score.
- However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score.
- Your final score is 11 - 2 = 9.
Example 2:
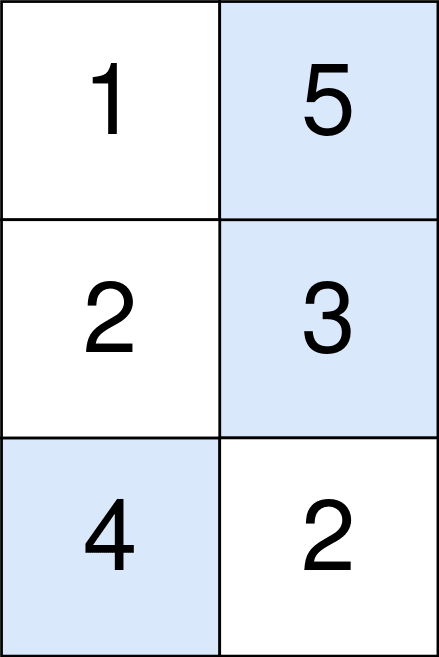
- Input: points = [[1,5],[2,3],[4,2]]
- Output: 11
-
Explanation:
- The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0).
- You add 5 + 3 + 4 = 12 to your score.
- However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score.
- Your final score is 12 - 1 = 11.
Constraints:
- m == points.length
- n == points[r].length
- 1 <= m, n <= 105
- 1 <= m * n <= 105
- 0 <= points[r][c] <= 105
Hint:
- Try using dynamic programming.
- dp[i][j] is the maximum number of points you can have if points[i][j] is the most recent cell you picked.
Solution:
We can break down the solution into several steps:
Step 1: Define the DP Array
We will use a 2D array dp where dp[i][j] represents the maximum points we can achieve by selecting the cell at row i and column j.
Step 2: Initialize the DP Array
Initialize the first row of dp to be the same as the first row of points since there are no previous rows to subtract the cost.
Step 3: Calculate DP Values for Each Row
For each subsequent row, we calculate the maximum possible points for each column considering the costs of switching from the previous row.
To efficiently calculate the transition from row i-1 to row i, we can use two auxiliary arrays left and right:
- left[j] will store the maximum value we can achieve for the j-th column considering only transitions from the left.
- right[j] will store the maximum value we can achieve for the j-th column considering only transitions from the right.
Step 4: Update DP for Each Row
For each column j in row i:
- Update dp[i][j] using the maximum of either left[j] or right[j] plus points[i][j].
Step 5: Return the Maximum Value from the Last Row
The result will be the maximum value in the last row of the dp array.
Let's implement this solution in PHP: 1937. Maximum Number of Points with Cost
Explanation:
- left and right arrays: These help us compute the maximum points we can gain for each cell by considering the previous row's values, efficiently accounting for the penalty from moving across columns.
- Dynamic programming approach: This method ensures that each row is calculated based on the previous row, making the solution scalable for large matrices.
This approach has a time complexity of (O(m times n)), which is efficient given the constraints.
Contact Links
If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks ?. Your support would mean a lot to me!
If you want more helpful content like this, feel free to follow me:
- GitHub
The above is the detailed content of Maximum Number of Points with Cost. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Alipay PHP SDK transfer error: How to solve the problem of 'Cannot declare class SignData'?
Apr 01, 2025 am 07:21 AM
Alipay PHP SDK transfer error: How to solve the problem of 'Cannot declare class SignData'?
Apr 01, 2025 am 07:21 AM
Alipay PHP...
 Explain JSON Web Tokens (JWT) and their use case in PHP APIs.
Apr 05, 2025 am 12:04 AM
Explain JSON Web Tokens (JWT) and their use case in PHP APIs.
Apr 05, 2025 am 12:04 AM
JWT is an open standard based on JSON, used to securely transmit information between parties, mainly for identity authentication and information exchange. 1. JWT consists of three parts: Header, Payload and Signature. 2. The working principle of JWT includes three steps: generating JWT, verifying JWT and parsing Payload. 3. When using JWT for authentication in PHP, JWT can be generated and verified, and user role and permission information can be included in advanced usage. 4. Common errors include signature verification failure, token expiration, and payload oversized. Debugging skills include using debugging tools and logging. 5. Performance optimization and best practices include using appropriate signature algorithms, setting validity periods reasonably,
 How does session hijacking work and how can you mitigate it in PHP?
Apr 06, 2025 am 12:02 AM
How does session hijacking work and how can you mitigate it in PHP?
Apr 06, 2025 am 12:02 AM
Session hijacking can be achieved through the following steps: 1. Obtain the session ID, 2. Use the session ID, 3. Keep the session active. The methods to prevent session hijacking in PHP include: 1. Use the session_regenerate_id() function to regenerate the session ID, 2. Store session data through the database, 3. Ensure that all session data is transmitted through HTTPS.
 Describe the SOLID principles and how they apply to PHP development.
Apr 03, 2025 am 12:04 AM
Describe the SOLID principles and how they apply to PHP development.
Apr 03, 2025 am 12:04 AM
The application of SOLID principle in PHP development includes: 1. Single responsibility principle (SRP): Each class is responsible for only one function. 2. Open and close principle (OCP): Changes are achieved through extension rather than modification. 3. Lisch's Substitution Principle (LSP): Subclasses can replace base classes without affecting program accuracy. 4. Interface isolation principle (ISP): Use fine-grained interfaces to avoid dependencies and unused methods. 5. Dependency inversion principle (DIP): High and low-level modules rely on abstraction and are implemented through dependency injection.
 How to debug CLI mode in PHPStorm?
Apr 01, 2025 pm 02:57 PM
How to debug CLI mode in PHPStorm?
Apr 01, 2025 pm 02:57 PM
How to debug CLI mode in PHPStorm? When developing with PHPStorm, sometimes we need to debug PHP in command line interface (CLI) mode...
 Framework Security Features: Protecting against vulnerabilities.
Mar 28, 2025 pm 05:11 PM
Framework Security Features: Protecting against vulnerabilities.
Mar 28, 2025 pm 05:11 PM
Article discusses essential security features in frameworks to protect against vulnerabilities, including input validation, authentication, and regular updates.
 How to automatically set permissions of unixsocket after system restart?
Mar 31, 2025 pm 11:54 PM
How to automatically set permissions of unixsocket after system restart?
Mar 31, 2025 pm 11:54 PM
How to automatically set the permissions of unixsocket after the system restarts. Every time the system restarts, we need to execute the following command to modify the permissions of unixsocket: sudo...
 What are Enumerations (Enums) in PHP 8.1?
Apr 03, 2025 am 12:05 AM
What are Enumerations (Enums) in PHP 8.1?
Apr 03, 2025 am 12:05 AM
The enumeration function in PHP8.1 enhances the clarity and type safety of the code by defining named constants. 1) Enumerations can be integers, strings or objects, improving code readability and type safety. 2) Enumeration is based on class and supports object-oriented features such as traversal and reflection. 3) Enumeration can be used for comparison and assignment to ensure type safety. 4) Enumeration supports adding methods to implement complex logic. 5) Strict type checking and error handling can avoid common errors. 6) Enumeration reduces magic value and improves maintainability, but pay attention to performance optimization.






