Program for Merge Sort in Java

Program for Merge Sort in Java is one of the most widely used and efficient algorithms. Merge sort is based on the divide and conquer technique which involves dividing a given problem into multiple subproblems and solving each subproblem independently. When the subproblems are solved, we combine their results to get the final solution to the problem. Merge sort algorithm can be implemented using recursion as it involves working with subproblems rather than the main problem.

How does the Merge Sort work?

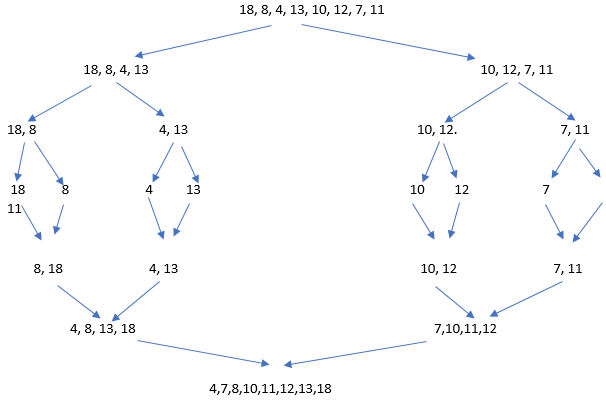
Let us consider an unsorted array that needs to be sorted using the merge sort algorithm. Here are the steps involved in sorting an array with values: 18, 8, 4, 13, 10, 12, 7, and 11:

Start Your Free Software Development Course

Web development, programming languages, Software testing & others

• The first step involves finding a pivot element on the basis of which our input array will be divided into subarrays.
• Let us consider that element 13 is chosen as the pivot; therefore, the original array will be divided into two subarrays. The first subarray will contain 18, 8, 4, 13, and the second subarray will contain the remaining elements 10, 12, 7, 11.
• Subarrays obtained in step 2 are further subdivided as in step 1, and this continues.
• Once the main array is divided into subarrays with single elements, we start merging these subarrays again in such that the merged elements are in sorted order.
• Here is how the actual divide and conquer works:

Program for Merge Sort in Java

Here is a code example showing the implementation of merge sort in java:

Code:

package com.edubca.sorting;
public class MergeSort {
private int[] array;
private int[] tempMergedArr;
private int length;
public static void main(String a[]){
int[] inputArr = {18, 8, 4, 13, 10, 12, 7, 11};
MergeSort mergeSort = new MergeSort();
mergeSort.sort(inputArr);
for(int i:inputArr){
System.out.print(i + " ");
}
}
public void sort(int inputArr[]) {
this.array = inputArr;
this.length = inputArr.length;
this.tempMergedArr = new int[length];
performMergeSort(0, length - 1);
}
private void performMergeSort(int lowerIndex, int higherIndex) {
if (lowerIndex < higherIndex) {
int middle = lowerIndex + (higherIndex - lowerIndex) / 2;
// Sort the left side of the array call performMergeSort recursively
performMergeSort(lowerIndex, middle);
// Sort the right side of the array call performMergeSort recursively
performMergeSort(middle + 1, higherIndex);
// Merge subparts using a temporary array
mergeData(lowerIndex, middle, higherIndex);
}
}
private void mergeData (int lowerIndex, int middle, int higherIndex) {
for (int i = lowerIndex; i <= higherIndex; i++) {
tempMergedArr[i] = array[i];
}
int i = lowerIndex;
int j = middle + 1;
int k = lowerIndex;
while (i <= middle && j <= higherIndex) {
if (tempMergedArr[i] <= tempMergedArr[j]) {
array[k] = tempMergedArr[i];
i++;
} else {
array[k] = tempMergedArr[j];
j++;
}
k++;
}
while (i <= middle) {
array[k] = tempMergedArr[i];
k++;
i++;
}
}
}

The above code will produce a sorted array as output.

Output:

When should we Use the Merge Sort?

Merge sort can be used in the following scenarios:

• When the data structure to be sorted does not support random access, then the merge sort can be helpful and efficient.
• When a high level of parallelism is required, merge sort can be used as different subproblems can be solved independently using multiple processes running in parallel.
• Merge sort is quicker when working with linked lists because pointers can easily be changed while merging the lists.
• Merge Sort can be considered a stable sort, meaning that the same element in an array maintains its original positions with respect to each other. In cases where high stability is required, one can go for merge sort. 

Complexity Analysis of Merge Sort

Below points analysis complexity of merge sort:

• Merge sort is a recursive algorithm, and its time complexity is O(n*log n) in all three cases (worst, best and average) as merge sort divides the array into two equal halves and takes linear time to merge them.
• Space Complexity of merge sort is O (n) as it operates on the recursive approach. Hence merge sort can be considered as a fast, space, and time-efficient algorithm.

Comparing Merge Sort with Other Algorithms

Below points compare merge sort with other algorithms:

• Heap Sort has the same time complexity as merge sort, but it requires only O (1) auxiliary space instead of merge sort’s O (n). Hence heap sort is more space-efficient than merge sort.
• Quick Sort implementations generally outperform merge sort for sorting RAM-based arrays.
• Merge sort outperforms quick sort and heap sort algorithms when working with the linked list as pointers can easily be changed.

Conclusion-Program for Merge Sort in Java

The article concludes that the merge sort is an important concept to understand when it comes to algorithms.

The above is the detailed content of Program for Merge Sort in Java. For more information, please follow other related articles on the PHP Chinese website!