
The Fibonacci Series in C# in the Fibonacci series is one of the famous sequence series. The sequence is 0, 1, 1, 2, 3, 5, 8…. The Fibonacci series starts from zero and one and the next number is the sum of two preceding numbers. It has been said that the Fibonacci Series created by Mr.Leonardo Pisano Bigollo in the 13th century. Fibonacci series is useful for some scenarios. Basically it was originally used to solve the rabbit problem i.e. The number of rabbits born from a pair. There are other problems also in which the Fibonacci sequence is useful.
As in the Fibonacci series, the number is the sum of its two preceding numbers. So if we have a Fibonacci series say 0, 1, 1, 2, 3, 5, 8, 13, 21… According to this next number would be the sum of its preceding two like 13 and 21. So the next number is 13+21=34.
Here is the logic for generating Fibonacci series
F(n)= F(n-1) +F(n-2)
Where F(n) is term number and F(n-1) +F(n-2) is a sum of preceding values.
So if we have series 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…
According to the logic F(n)= F(n-1) +F(n-2)
F(n)= 55+89
F(n)= 144
The next term would be 144.
Fibonacci series can be generated in multiple ways.
This way is the easiest way to generate series.
Code:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespaceFibonacciDemo
{
classProgram
{
staticint Fibonacci(int n)
{
intfirstnumber = 0, secondnumber = 1, result = 0;
if (n == 0) return 0; //It will return the first number of the series
if (n == 1) return 1; // it will return the second number of the series
for (int i = 2; i<= n; i++) // main processing starts from here
{
result = firstnumber + secondnumber;
firstnumber = secondnumber;
secondnumber = result;
}
return result;
}
staticvoid Main(string[] args)
{
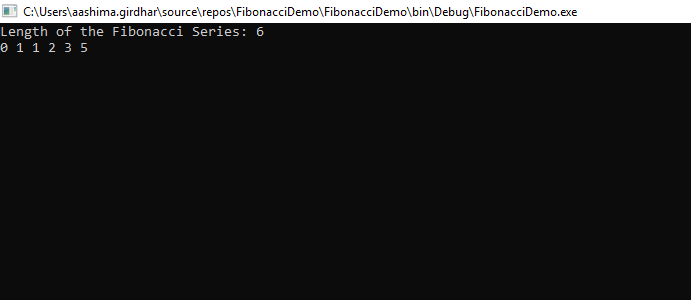
Console.Write("Length of the Fibonacci Series: ");
int length = Convert.ToInt32(Console.ReadLine());
for(int i = 0; i< length; i++)
{
Console.Write("{0} ", Fibonacci(i));
}
Console.ReadKey();
}
}
}This is another method to solve this problem.
Method 1
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespaceFibonacciDemo
{
classProgram
{
staticint Fibonacci(int n)
{
intfirstnumber = 0, secondnumber = 1, result = 0;
if (n == 0) return 0; //it will return the first number of the series
if (n == 1) return 1; // it will return the second number of the series
return Fibonacci(n-1) + Fibonacci(n-2);
}
staticvoid Main(string[] args)
{
Console.Write("Length of the Fibonacci Series: ");
int length = Convert.ToInt32(Console.ReadLine());
for(int i = 0; i< length; i++)
{
Console.Write("{0} ", Fibonacci(i));
}
Console.ReadKey();
}
}
}Method 2
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace FibonacciSeries
{
class Program
{
public static void Fibonacci
(
int firstnumber,
int secondnumber,
int count,
int length,
)
{
if (count <= length)
{
Console.Write("{0} ", firstnumber);
Fibonacci(secondnumber, firstnumber + secondnumber, count + 1, length);
}
}
public static void Main(string[] args)
{
Console.Write("Length of the Fibonacci Series: ");
int length = Convert.ToInt32(Console.ReadLine());
Fibonacci(0, 1, 1, length);
Console.ReadKey();
}
}
}Output:
Code:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
public class Program
{
public static int[] Fibonacci(int number)
{
int[] a = new int[number];
a[0] = 0;
a[1] = 1;
for (int i = 2; i < number; i++)
{
a[i] = a[i - 2] + a[i - 1];
}
return a;
}
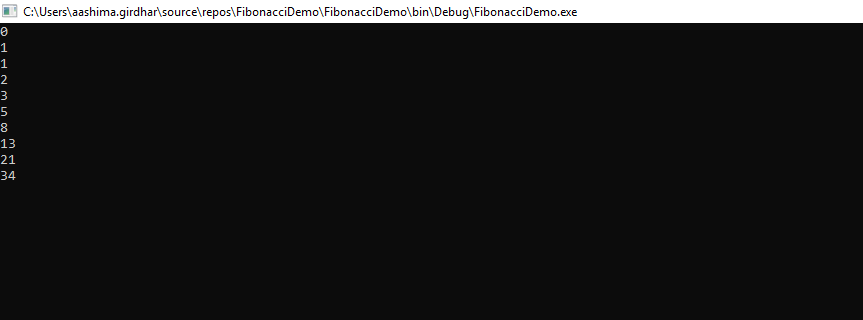
public static void Main(string[] args)
{
var b = Fibonacci(10);
foreach (var elements in b)
{
Console.WriteLine(elements);
}
}
}Output:
Following are the methods
Code:
using System;
namespace FibonacciSeries
{
class Program {
public static int NthTerm(int n)
{
if ((n == 0) || (n == 1))
{
return n;
}
else
{
return (NthTerm(n - 1) + NthTerm(n - 2));
}
}
public static void Main(string[] args)
{
Console.Write("Enter the nth term of the Fibonacci Series: ");
int number = Convert.ToInt32(Console.ReadLine());
number = number - 1;
Console.Write(NthTerm(number));
Console.ReadKey();
}
}
}The above code is to find the nth term in the Fibonacci series. For example, if we want to find the 12th term in the series then the result would be 89.
(O(Log t) Time).
There is one another recurrence formula that can be used to find t’th Fibonacci Number If t is even then = t/2:
F(t) = [2*F(k-1) + F(k)]*F(k)
If t is odd then k = (t + 1)/2
F(t) = F(k)*F(k) + F(k-1)*F(k-1)
Fibonacci matrix
After getting determinant, we will get (-1)t = Ft+1Ft-1 – Ft2
FmFt + Fm-1Ft-1 = Fm+t-1
By putting t = t+1,
FmFt+1 + Fm-1Ft = Fm+t
Putting m = t
F2t-1 = Ft2 + Ft-12
F2t = (Ft-1 + Ft+1)Ft = (2Ft-1 + Ft)Ft
To get the formula we will do the following
If t is even, put k = t/2
If t is odd, put k = (t+1)/2
So by sorting these numbers we can prevent the constantly using memory space of STACK. It gives time complexity of O(n). The recursive algorithm is less efficient.
Code:
int f(n) : if( n==0 || n==1 ) return n; else return f(n-1) + f(n-2)
Now when the above algorithm run for n=4
fn(4)
f(3) f(2)
f(2) f(1) f(1) f(0)
f(1) f(0)
So it’s a tree. For calculating f(4) we need to calculate f(3) and f(2) and so on.For a small value of 4, f(2) is calculated twice and f(1) is calculated thrice. This number of additions will grows for large numbers.
There is a conjecture that the number of additions required for calculating f (n) is f (n+1) -1.
Here the iteration method is always preferred because it has a faster approach to solve this kind of problem. Here we are storing the first and the second number of Fibonacci series in the previous number and previous number(these are two variables) and also we are using the current number to store the Fibonacci number.
The above is the detailed content of Fibonacci Series in C#. For more information, please follow other related articles on the PHP Chinese website!




