Foreword
In the previous article , we explained the expansion and erosion functions in image processing. This article will do the edge gradient calculation function.
Edge of the image
How are the edges of images expressed mathematically?

On the edges of the image, adjacent pixel values should change significantly. In mathematics, derivatives are a way to express the speed of change. Large changes in gradient values indicate significant changes in the content of the image.
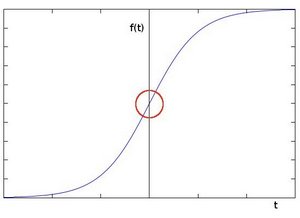
To explain with a more vivid image, suppose we have a one-dimensional graph. The "jump" in the gray value in the image below indicates the existence of an edge:
Using first-order differential derivation, we can more clearly see the existence of the edge "jump" (shown here as a high peak):
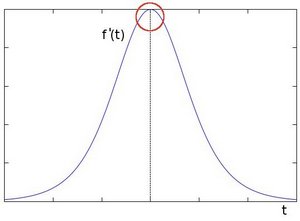
From this we can conclude that edges can be found by locating pixels with gradient values greater than those of the neighborhood.
Approximate gradient
For example, when the core is 3.
First calculate the approximate derivative in the x direction:

Then calculate the approximate derivative for the y direction:

Then calculate the gradient:

Of course you can also write:
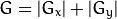
Function implementation
The code is as follows:
var Sobel = function(__src, __xorder, __yorder, __size, __borderType, __dst){
(__src && (__xorder ^ __yorder)) || error(arguments.callee, IS_UNDEFINED_OR_NULL/* {line} * /);
if(__src.type && __src.type === "CV_GRAY"){
var kernel1,
kernel2,
height = __src.row,
width = __src. col,
dst = __dst || new Mat(height, width, CV_16I, 1),
dstData = dst.data
size = __size || 3;
switch(size){
case 1:
size = 3;
case 3:
if(__xorder){
kernel = [-1, 0, 1,
-2, 0, 2,
-1, 0, 1
];
}else if(__yorder){
kernel = [-1, -2, -1,
, 0, 0,
, 2 , 1
];
}
break;
case 5:
if(__xorder){
kernel = [-1, -2, 0, 2, 1,
-4, -8, 0, 8, 4,
-6,-12, 0,12, 6,
-4, -8, 0, 8, 4,
-1, - 2, 0, 2, 1
];
}else if(__yorder){
kernel = [-1, -4, -6, -4, -1,
-2, - 8,-12, -8, -2,
, 0, 0, 0, 0,
, 8, 12, 8, 2,
, 4, 6, 4, 1
] ;
}
break;
default:
error(arguments.callee, UNSPPORT_SIZE/* {line} */);
}
GRAY216IC1Filter(__src , size, height, width, kernel, dstData, __borderType);
}else{
error(arguments.callee, UNSPPORT_DATA_TYPE/* {line} */);
}
return dst;
};
Only Sobel operators with kernel sizes of 3 and 5 are provided here. The main reason is that the calculation of kernels of 7 or above is relatively slow.
Output a single-channel 16-bit signed integer matrix.
The code is as follows:
function GRAY216IC1Filter(__src, size, height, width, kernel, dstData, __borderType){
var start = size >> 1;
var withBorderMat = copyMakeBorder(__src, start, start, 0, 0, __borderType);
var mData = withBorderMat.data,
mWidth = withBorderMat.col;
var i, j, y, x, c;
var newValue, nowX, offsetY, offsetI;
for(i = height; i--;){
offsetI = i * width;
for(j = width; j- -;){
newValue = 0;
for(y = size; y--;){
offsetY = (y i) * mWidth;
for(x = size; x--; ){
nowX = x j;
newValue = (mData[offsetY nowX] * kernel[y * size x]);
}
}
dstData[j offsetI] = newValue;
}
}
}
Then give the kernel and matrix to this filter, and it’s OK.
The reason for making this filter independent is that it can be used for other similar calculation edge functions, such as Laplacian and Scharr operators.
Convert to unsigned 8-bit integer
Since the Sobel operator calculates a 16-bit signed integer and cannot be displayed as a picture, we need a function to convert it into an unsigned 8-bit integer matrix.
The convertScaleAbs function takes the absolute value of each element and puts it into the Int8Array array. Since numbers greater than 255 will be automatically converted to 255 during assignment, and numbers less than 0 will be automatically converted to 0, so We don't need to make a function to take care of this work.
function convertScaleAbs(__src, __dst){
__src || error(arguments.callee, IS_UNDEFINED_OR_NULL/* {line} */);
var height = __src.row,
width = __src.col,
channel = __src.channel,
sData = __src.data;
if(!__dst){
if(channel === 1)
dst = new Mat(height, width, CV_GRAY);
else if(channel === 4)
dst = new Mat(height, width, CV_RGBA);
else
dst = new Mat(height, width, CV_8I, channel);
}else{
dst = __dst;
}
var dData = dst.data;
var i, j, c;
for(i = height; i--; ){
for(j = width * channel; j--;){
dData[i * width * channel j] = Math.abs(sData[i * width * channel j]);
}
}
return dst;
}
Merge values proportionally
We also need a function to superimpose the x-direction gradient calculation value and the y-direction gradient calculation value.
var addWeighted = function(__src1, __alpha, __src2, __beta , __gamma, __dst){
(__src1 && __src2) || error(arguments.callee, IS_UNDEFINED_OR_NULL/* {line} */);
var height = __src1.row,
width = __src1.col ,
alpha = __alpha || 0,
beta = __beta || 0,
channel = __src1.channel,
gamma = __gamma || 0;
if(height !== __src2 .row || width !== __src2.col || channel !== __src2.channel){
error(arguments.callee, "Src2 must be the same size and channel number as src1!"/* {line} */);
return null;
}
if(!__dst){
if(__src1.type.match(/CV_d /))
dst = new Mat( height, width, __src1.depth(), channel);
else
dst = new Mat(height, width, __src1.depth());
}else{
dst = __dst;
}
var dData = dst.data,
s1Data = __src1.data,
s2Data = __src2.data;
var i;
for (i = height * width * channel; i--;)
dData[i] = __alpha * s1Data[i] __beta * s2Data[i] gamma;
return dst;
};
This function is very simple. It actually just adds the corresponding elements of two matrices in a fixed ratio.
Rendering