 Web Front-end
Web Front-end
 JS Tutorial
JS Tutorial
 Calendar Query Algorithm How to Calculate the Day of the Week a Certain Day Is_Basic Knowledge
Calendar Query Algorithm How to Calculate the Day of the Week a Certain Day Is_Basic Knowledge
Calendar Query Algorithm How to Calculate the Day of the Week a Certain Day Is_Basic Knowledge
How to calculate what day of the week a certain day is?
——Zeller's formula
What day of the week is a certain day in history? What day of the week is it in the future? Regarding this problem, there are many calculation formulas (two general calculation formulas and some piecewise calculation formulas), the most famous of which is the Zeller formula. That is, w=y [y/4] [c/4]-2c [26(m 1)/10] d-1
The symbols in the formula have the following meanings, w: week; c: century-1 ; y: year (two digits); m: month (m is greater than or equal to 3, less than or equal to 14, that is, in the Zeiler formula, January and February of a certain year are calculated as the 13th and 14th of the previous year. , for example, January 1, 2003 should be calculated as December 1, 2002); d: day; [ ] represents rounding, that is, only the integer part is required. (C is the century minus one, y is the last two digits of the year, M is the month, and d is the day. January and February should be calculated according to the 13th and 14th months of the previous year. At this time, C and y are both calculated as One year value. )
The calculated W is divided by 7, and the remainder is the day of the week. If the remainder is 0, it is Sunday.
Taking October 1, 2049 (the 100th anniversary of the National Day) as an example, use the Zeller formula to calculate. The process is as follows:
Zeller formula: w=y [y/ 4] [c/4]-2c [26(m 1)/10] d-1
=49 [49/4] [20/4]-2×20 [26× (10 1)/10] 1-1
=49 [12.25] 5-40 [28.6]
=49 12 5-40 28
=54 (divided by 7, the remainder is 5)
That is, October 1, 2049 ( The 100th National Day) is Friday.
What day of the week is your birthday (when you were born, this year, next year)? Might as well give it a try.
However, the above formula is only suitable for the situation after October 15, 1582 (the Pope at that time changed the Julian calendar established by Caesar to the Gregorian calendar, which is the Gregorian calendar used today).
Derivation of the process: (Those who are not interested in reasoning can skip it)
The week system is a system with ancient traditions. It is said that because the Bible Genesis stipulates that God took six days to create the world and rested on the seventh day, people also arrange their work and life based on a seven-day cycle, and Sunday is a day of rest. From a practical point of view, a cycle of seven days is more appropriate. Therefore, although China's traditional work cycle is ten days (for example, Wang Bo's "Tengwang Pavilion Preface" said "Ten Ten Days of Rest", which means that officials work every ten days as a cycle and take a holiday on the tenth day), but later also adopted Western week system.
In daily life, we often encounter the problem of knowing what day of the week a certain day is. Sometimes, we also want to know what day of the week a certain day in history was. Usually, the effective way to solve this problem is to look at the calendar, but we never carry a calendar with us at all times, let alone a perpetual calendar that has thousands of years of history. If you want to calculate the day of the week that a certain day is in computer programming, it is even more unrealistic to save a perpetual calendar in advance. At this time, is there any way to use some formula to deduce the day of the week from the year, month and day?
The answer is yes. In fact, we often do this too. Let's start with a simple example. For example, if you know that May 1, 2004 is a Saturday, then it is not difficult to calculate the day of the week when "World No Tobacco Day" is on May 31, 2004. We can count on our fingers from the 1st to the 31st, and at the same time count the weeks, and finally we can count that May 31st is Monday.
In fact, when you use mathematical calculations, you don’t have to use your fingers. We know that weeks come around in a cycle of seven days, so May 1st is a Saturday, and seven days later, May 8th is also a Saturday. In terms of dates, 8-1=7, which is a multiple of 7. Similarly, May 15th, May 22nd, and May 29th are also Saturdays, and the differences between their dates and May 1st are 14, 21, and 28 respectively, which are also multiples of 7. What about May 31st? 31-1=30, although it is not a multiple of 7, but 31 divided by 7, the remainder is 2.
This means that the week of May 31st is two days after the week of May 1st. Two days after Saturday it is Monday.
This simple calculation tells us a basic idea for calculating the week: First, you need to know the day of the week that is a certain day before the day you want to calculate, and use this day as the standard for calculation, that is Equivalent to the "origin" of a calculation.Secondly, know how many days are the difference between the day you want to calculate and the determined day, divide the difference of this date by 7, and the remainder indicates how many days after the week of the determined day the day you want to calculate is. If the remainder is 0, it means that the days of the two days are the same. Obviously, if the day as the "origin" is selected as Sunday, then the remainder will be exactly equal to the day of the week, making the calculation more convenient.
But directly calculating the number of days between two days is still cumbersome. For example, the distance between July 29, 1982 and May 1, 2004 is 7947 days, which cannot be calculated at once. It includes three periods of time: first, the remaining days in the year after July 29, 1982; second, the total number of days in the twenty-one full years from 1983 to 2003; third, the period from New Year's Day to May 1, 2004 number of days. The second period is easier to calculate. It is equal to 21*365 5 = 7670 days. The reason why 5 is added is because there are 5 leap years during this period. The first and third paragraphs are more troublesome. For example, in the third paragraph, you need to add up the number of days in the four months before May, plus the date value, that is, 31 29 31 30 1 = 122 days. Similarly, the
paragraph needs to add up the number of days in the five months after July, plus the number of remaining days in July, a total of 155 days.
So the total number of days apart is 122 7670 155 = 7947 days.
Think about it carefully, if the date of "origin" is selected as December 31st, then the first period will be a whole year. In this way, the first period and the second period will be It can be combined and calculated so that the total for the entire year is exactly equal to the year difference between the two days minus one. If the "origin" date is further selected as December 31, 1 BC (or December 31, AD 0 as used by astronomers), the total number of the entire year will be exactly the year of the day you want to count minus one. After this simplification, you only need to calculate two periods of time: first, the total number of days in so many whole years; second, the day you want to calculate is the day of the year. Coincidentally, according to the year and month settings of the Gregorian calendar, and working backwards, December 31, 1 BC, happened to be a Sunday. That is to say, the remainder of the total number of days calculated in this way divided by 7 happened to be the day of the week. So the question now is
only one: how many leap years are there in so many whole years. This requires understanding the leap rules of the Gregorian calendar.
We know that the Gregorian calendar has 365 days in an ordinary year and 366 days in a leap year. The method of setting leaps is to add one day in February for years that are evenly divisible by 4, but there are no leaps for years that are evenly divisible by 100, and there are leaps for years that are evenly divisible by 400. Therefore, years like 1600, 2000, and 2400 are all leap years, while years 1700, 1800, 1900, and 2100 are ordinary years. 1 BC is also a leap year according to the Gregorian calendar.
Therefore, for the number of leap years in all whole years from December 31, 1 BC (or 0 AD) to a certain day in year Y, it is equal to
[(Y -1)/4] - [(Y-1)/100] [(Y-1)/400],
[...] means only taking the integer part. The first item indicates the need to add the number of years divisible by 4, the second item indicates the need to remove the number of years divisible by 100, and the third item indicates the need to add the number of years divisible by 400. The reason why Y needs to be reduced by one is that
we get the first formula to calculate the day of the week a certain day is:
W = (Y-1)*365 [(Y-1) /4] - [(Y-1)/100] [(Y-1)/400] D. (1)
where D is the cumulative number of days of this day in this year. The calculated W is the number of days between December 31, 1 BC (or AD 0) and this day. Divide W by 7, what is the remainder, and this day is the day of the week. For example, let’s calculate May 1, 2004:
W = (2004-1)*365 [(2004-1)/4] - [(2004-1)/100] [(2004-1 )/400] (31 29 31 30 1) = 731702,
731702 / 7 = 104528...6, the remainder is six, indicating that this day is Saturday. This is consistent with the facts.
Although the above formula (1) is very accurate, the calculated number is too large and it is very inconvenient to use. If you think about it carefully, in fact, the number of days W is used is just to get the remainder after dividing it by 7. This inspires us to simplify this W value. We only need to find a smaller number that is the same as its remainder. In number theory terms, it is to find a smaller positive integer that is congruent with it. It can still be done. Calculate the exact number of weeks.
Obviously, the reason why W is so large is because the first term (Y-1)*365 in the formula is too large. In fact,
(Y-1)*365 = (Y-1) * (364 1)
= (Y-1) * (7*52 1)
= 52 * (Y -1) * 7 (Y-1),
The first term of this result is a multiple of 7, and the remainder when divided by 7 is 0, so the remainder of (Y-1)*365 divided by 7 is actually It is equal to the remainder of Y-1 divided by 7. This relationship can be expressed as:
(Y-1)*365 ≡ Y-1 (mod 7).
Among them, ≡ is the symbol indicating congruence in number theory. Mod 7 means that when 7 is used as the modulus (that is, the divisor), the numbers on both sides of the ≡ sign are congruent. Therefore, (Y-1) can be used to replace (Y-1)*365, so that we get the famous and most common formula for calculating the days of the week:
W = (Y- 1) [(Y-1)/4] - [(Y-1)/100] [(Y-1)/400] D. (2)
Although this formula is much easier to use, it is not the most useful formula because the calculation of the cumulative number of days D is also troublesome
. Can it be calculated directly using the month number and date? The answer is also yes.We might as well observe the number of days in each
month, the list is as follows:
Month: January, February, March, April, May, June, July, August, September, October, November, December
------------------------------------------------ --------------------------
Number of days: 31 28(29) 31 30 31 30 31 31 30 31 30 31
If you subtract 28 (=4*7) from this number of days, it will not affect the remainder value of W divided by 7. In this way we get another
table:
Month: January, February, March, April, May, June, July, August, September, October, November, December
--- -------------------------------------------------- ------------------
Number of remaining days: 3 0(1) 3 2 3 2 3 3 2 3 2 3
Normal year accumulation: 3 3 6 8 11 13 16 19 21 24 26 29
Leap year accumulation: 3 4 7 9 12 14 17 20 22 25 27 30
If you look closely, we will find that excluding January and February, March to July The remaining days in the five months of January are 3,2,3,2,3; the days in the five months from August to December are also 3,2,3,2,3, which is exactly a repetition. Among the corresponding accumulated days, the difference between the accumulated days in the next month and the accumulated days in the previous month minus 28 is this repetition. It is precisely because of the existence of this rule that the cumulative number of days in ordinary years and leap years can be easily expressed by mathematical formulas:
╭ d; (when M = 1)
D = { 31 d; (when M=2) (3)
╰ [ 13 * (M 1) / 5 ] - 7 (M-1) * 28 d i. (When M≥3)
Where [...] still means taking only the integer part; M and d are the month and day of the day you want to calculate respectively; i=0 in ordinary years and i=1 in leap years. The expression M≥3 needs to be explained: [13*(M 1)/5]-7 is calculated as the average annual cumulative value in the second table above. Adding (M-1)*28 means Counts the total number of days in all months preceding the month of days. This is a very clever way to use rounding operations to realize the cycle of 3,2,3,2,3. For example, for May 1, 2004, there is:
D = [ 13 * (5 1) / 5 ] - 7 (5-1) * 28 1 1
= 122,
This is exactly the cumulative number of days on May 1st in 2004.
Suppose we make another change and treat January and February as the "13th" and "14th" of the previous year. Not only does it still comply with this formula, but also because of this, leap days become The last day of the previous "year" (a total of 14 months) becomes part of d, so the impact of leap years is also removed, and the formula is simplified to:
D = [ 13 * (M 1) / 5 ] - 7 (M-1) * 28 d. (3≤M≤14) (4)
The above formula for calculating the days of the week can be further simplified to:
W = (Y-1) [(Y-1)/ 4] - [(Y-1)/100] [(Y-1)/400] [ 13 * (M 1) / 5 ] - 7 (M-1) * 28 d.
Because -7 and (M-1)*28 are both divisible by 7, so if these two items are removed, the remainder after dividing W by 7 remains unchanged, and the formula becomes:
W = (Y-1) [(Y-1)/4] - [(Y-1)/100] [(Y-1)/400] [ 13 * (M 1) / 5 ] d. (5)
Of course, it should be noted that January and February have been regarded as the 13th and 14th months of the previous year. Therefore, when calculating the weeks of the days in January and February, except M, press When counting 13 or 14, year Y also needs to be subtracted by one. For example, January 1, 2004 is Thursday. Use this formula to calculate:
W = (2003-1) [(2003-1)/4] - [(2003-1)/100 ] [(2003-1)/400] [13*(13 1)/5]
1
= 2002 500 - 20 5 36 1
= 2524;
2524 / 7 = 360… …4. This is consistent with reality.
Formula (5) is already a formula for calculating the day of the week from the year, month, and day, but it is not the most concise. There are still ways to improve the processing of years. Let’s first use this formula to calculate the week on March 1st in the first year of each century. The list is as follows:
Year: 1(401,801,…,2001) 101(501,901,…,2101)
-------------------------------------------------- ------------------
Week: 4 2
====================== ========================
Year: 201(601,1001,…,2201) 301(701,1101,…,2301)
------------------------------------------------ --------------------
Week: 0 5
It can be seen that this week repeats itself every four centuries. If we regard the week number of March 1, 301 (701, 1101,..., 2301) as -2 (according to the definition of remainder in number theory, -2 is the same as the remainder of 5 divided by 7, so it can be done like this transformation), then this repeating sequence is exactly an arithmetic sequence of 4,2,0,-2. Based on this, we can get the following formula for calculating the day of the week on March 1 of the first year of each century:
W = (4 - C mod 4) * 2 - 4. (6)
In the formula, C is the century number of the century minus one, and mod represents the modulo operation, that is, finding the remainder. For example, for March 1, 2001, C=20, then:
W = (4 - 20 mod 4) * 2 - 4
= 8 - 4
= 4.
Substituting formula (6) into formula (5), after transformation, we can get:
(Y-1) [(Y-1)/4] - [(Y-1) /100] [(Y-1)/400] ≡ (4 - C mod 4) * 2 - 1
(mod 7). (7)
Therefore, (Y-1) [(Y-1)/4] - [(Y-1)/100] [(Y-1)/400] in formula (5) These four terms can be replaced by (4 - C mod 4) * 2 - 1 when calculating the day of the week in the first year of each century. This formula is written as:
W = (4 - C mod 4) * 2 - 1 [13 * (M 1) / 5] d. (8)
With the formula for calculating the date and week of the first year of each century, the formula for calculating the date and week of the other years of the century is easy to obtain.Because in a century, the year ending with 00 is the last year, so there is no need to consider the rule of "no leaps in one hundred years, and leaps in four hundred years", only the rule of "one leap in four years". Following the method of simplifying formula (1) to formula (2), we can easily get a simpler formula from formula (8) than formula (5) to calculate the day of the week for any day:
W = (4 - C mod 4) * 2 - 1 (y-1) [y/4] [13 * (M 1) / 5] d. (9)
Where, y is the last two digits of the year.
If we consider that the modulo operation is not the four arithmetic operations, we can further rewrite (4 - C mod 4) * 2 into an expression that only contains the four arithmetic operations. Because there is the following relationship between the quotient q and the remainder r of the century minus one C divided by 4:
4q r = C,
where r is C mod 4, therefore, there is :
r = C - 4q
= C - 4 * [C/4]. (10)
then
(4 - C mod 4) * 2 = (4 - C 4 * [C/4]) * 2
= 8 - 2C 8 * [ C/4]
≡ [C/4] - 2C 1 (mod 7). (11)
Substituting equation (11) into (9), we get:
W = [C/4] - 2C y [y/4] [13 * (M 1) / 5] d - 1. (12)
This formula can calculate W by subtracting one from the century, the last two digits of the year, the month and the day, and then divide it by 7. The remainder obtained indicates the day of the week. The only requirement is The modification is to treat January and February as the 13th and 14th months of the previous year, and both C and y are valued according to the year of the previous year. Therefore, it is generally considered to be the best formula for calculating the day of the week for any given day. This formula was first derived by the German mathematician Christian Zeller (1822-1899) in 1886, so it is commonly known as Zeller's Formula. To facilitate oral arithmetic, [13 * (M 1) / 5] in the formula is often written as [26 * (M 1) / 10].
Now let us still calculate the week of May 1, 2004. Obviously C=20, y=4, M=5, d=1. Substitute into Zeiler's
formula, we have:
W = [20/4] - 40 4 1 [13 * (5 1) / 5] 1 - 1
= -15.
Note that the remainder of a negative number cannot be calculated according to the customary concept of remainder, but can only be calculated according to the definition of remainder in number theory. In order to facilitate calculation, we can add an integer multiple of 7 to it to make it a positive number. For example, adding 70, we get 55. Divide it by 7 again, and the remainder is 6, indicating that this day is Saturday. This is consistent with reality and consistent with the results calculated by formula (2).
Finally, it should be noted that the above formulas are all based on the leap rules of the Gregorian calendar. For the Julian calendar, Zeiler also derived the corresponding formula:
W = 5 - C y [y/4] [13 * (M 1) / 5] d - 1. (13)
In this way, we finally solved the problem of calculating the day of the week for any day without consulting the calendar once and for all.

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Replace String Characters in JavaScript
Mar 11, 2025 am 12:07 AM
Replace String Characters in JavaScript
Mar 11, 2025 am 12:07 AM
Detailed explanation of JavaScript string replacement method and FAQ This article will explore two ways to replace string characters in JavaScript: internal JavaScript code and internal HTML for web pages. Replace string inside JavaScript code The most direct way is to use the replace() method: str = str.replace("find","replace"); This method replaces only the first match. To replace all matches, use a regular expression and add the global flag g: str = str.replace(/fi
 Custom Google Search API Setup Tutorial
Mar 04, 2025 am 01:06 AM
Custom Google Search API Setup Tutorial
Mar 04, 2025 am 01:06 AM
This tutorial shows you how to integrate a custom Google Search API into your blog or website, offering a more refined search experience than standard WordPress theme search functions. It's surprisingly easy! You'll be able to restrict searches to y
 8 Stunning jQuery Page Layout Plugins
Mar 06, 2025 am 12:48 AM
8 Stunning jQuery Page Layout Plugins
Mar 06, 2025 am 12:48 AM
Leverage jQuery for Effortless Web Page Layouts: 8 Essential Plugins jQuery simplifies web page layout significantly. This article highlights eight powerful jQuery plugins that streamline the process, particularly useful for manual website creation
 Build Your Own AJAX Web Applications
Mar 09, 2025 am 12:11 AM
Build Your Own AJAX Web Applications
Mar 09, 2025 am 12:11 AM
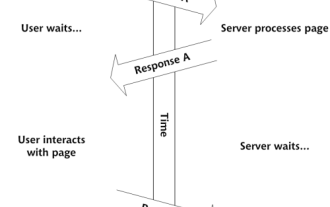
So here you are, ready to learn all about this thing called AJAX. But, what exactly is it? The term AJAX refers to a loose grouping of technologies that are used to create dynamic, interactive web content. The term AJAX, originally coined by Jesse J
 What is 'this' in JavaScript?
Mar 04, 2025 am 01:15 AM
What is 'this' in JavaScript?
Mar 04, 2025 am 01:15 AM
Core points This in JavaScript usually refers to an object that "owns" the method, but it depends on how the function is called. When there is no current object, this refers to the global object. In a web browser, it is represented by window. When calling a function, this maintains the global object; but when calling an object constructor or any of its methods, this refers to an instance of the object. You can change the context of this using methods such as call(), apply(), and bind(). These methods call the function using the given this value and parameters. JavaScript is an excellent programming language. A few years ago, this sentence was
 10 Mobile Cheat Sheets for Mobile Development
Mar 05, 2025 am 12:43 AM
10 Mobile Cheat Sheets for Mobile Development
Mar 05, 2025 am 12:43 AM
This post compiles helpful cheat sheets, reference guides, quick recipes, and code snippets for Android, Blackberry, and iPhone app development. No developer should be without them! Touch Gesture Reference Guide (PDF) A valuable resource for desig
 Improve Your jQuery Knowledge with the Source Viewer
Mar 05, 2025 am 12:54 AM
Improve Your jQuery Knowledge with the Source Viewer
Mar 05, 2025 am 12:54 AM
jQuery is a great JavaScript framework. However, as with any library, sometimes it’s necessary to get under the hood to discover what’s going on. Perhaps it’s because you’re tracing a bug or are just curious about how jQuery achieves a particular UI
 How do I create and publish my own JavaScript libraries?
Mar 18, 2025 pm 03:12 PM
How do I create and publish my own JavaScript libraries?
Mar 18, 2025 pm 03:12 PM
Article discusses creating, publishing, and maintaining JavaScript libraries, focusing on planning, development, testing, documentation, and promotion strategies.





