邻接矩阵prim:php实现图的邻接矩阵及普里姆(prim算法),弗洛伊德(floyd),迪杰斯特拉(dijkstra)算法
require 'mgraph.php';
$a = array('a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i');
$b = array('ab'=>'10', 'af'=>'11', 'bg'=>'16', 'fg'=>'17', 'bc'=>'18', 'bi'=>'12', 'ci'=>'8', 'cd'=>'22', 'di'=>'21', 'dg'=>'24', 'gh'=>'19', 'dh'=>'16', 'de'=>'20', 'eh'=>'7','fe'=>'26');//键为边,值权值
$test = new mgraph($a, $b);
print_r($test->prim());
?>
mgraph.php
/**
* php 实现图邻接矩阵
*
* @author zhaojiangwei
* @since 2011/10/31 17:23
*/
class mgraph{
private $vexs; //顶点数组
private $arc; //边邻接矩阵,即二维数组
private $arcdata; //边的数组信息
private $direct; //图的类型(无向或有向)
private $haslist; //尝试遍历时存储遍历过的结点
private $queue; //广度优先遍历时存储孩子结点的队列,用数组模仿
private $infinity = 65535;//代表无穷,即两点无连接,建带权值的图时用,本示例不带权值
private $primvexs; //prim算法时保存顶点
private $primarc; //prim算法时保存边
private $krus;//kruscal算法时保存边的信息
public function mgraph($vexs, $arc, $direct = 0){
$this->vexs = $vexs;
$this->arcdata = $arc;
$this->direct = $direct;
$this->initalizearc();
$this->createarc();
}
private function initalizearc(){
foreach($this->vexs as $value){
foreach($this->vexs as $cvalue){
$this->arc[$value][$cvalue] = ($value == $cvalue ? 0 : $this->infinity);
}
}
}
//创建图 $direct:0表示无向图,1表示有向图
private function createarc(){
foreach($this->arcdata as $key=>$value){
$strarr = str_split($key);
$first = $strarr[0];
$last = $strarr[1];
$this->arc[$first][$last] = $value;
if(!$this->direct){
$this->arc[$last][$first] = $value;
}
}
}
//floyd算法
public function floyd(){
$path = array();//路径数组
$distance = array();//距离数组
foreach($this->arc as $key=>$value){
foreach($value as $k=>$v){
$path[$key][$k] = $k;
$distance[$key][$k] = $v;
}
}
for($j = 0; $j vexs); $j ++){
for($i = 0; $i vexs); $i ++){
for($k = 0; $k vexs); $k ++){
if($distance[$this->vexs[$i]][$this->vexs[$k]] > $distance[$this->vexs[$i]][$this->vexs[$j]] + $distance[$this->vexs[$j]][$this->vexs[$k]]){
$path[$this->vexs[$i]][$this->vexs[$k]] = $path[$this->vexs[$i]][$this->vexs[$j]];
$distance[$this->vexs[$i]][$this->vexs[$k]] = $distance[$this->vexs[$i]][$this->vexs[$j]] + $distance[$this->vexs[$j]][$this->vexs[$k]];
}
}
}
}
return array($path, $distance);
}
//djikstra算法
public function dijkstra(){
$final = array();
$pre = array();//要查找的结点的前一个结点数组
$weight = array();//权值和数组
foreach($this->arc[$this->vexs[0]] as $k=>$v){
$final[$k] = 0;
$pre[$k] = $this->vexs[0];
$weight[$k] = $v;
}
$final[$this->vexs[0]] = 1;
for($i = 0; $i vexs); $i ++){
$key = 0;
$min = $this->infinity;
for($j = 1; $j vexs); $j ++){
$temp = $this->vexs[$j];
if($final[$temp] != 1 && $weight[$temp] $key = $temp;
$min = $weight[$temp];
}
}
$final[$key] = 1;
for($j = 0; $j vexs); $j ++){
$temp = $this->vexs[$j];
if($final[$temp] != 1 && ($min + $this->arc[$key][$temp]) $pre[$temp] = $key;
$weight[$temp] = $min + $this->arc[$key][$temp];
}
}
}
return $pre;
}
//kruscal算法
private function kruscal(){
$this->krus = array();
foreach($this->vexs as $value){
$krus[$value] = 0;
}
foreach($this->arc as $key=>$value){
$begin = $this->findroot($key);
foreach($value as $k=>$v){
$end = $this->findroot($k); 本文链接http://www.cxybl.com/html/wlbc/Php/20120607/28507.html

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
 What are the differences between Huawei GT3 Pro and GT4?
Dec 29, 2023 pm 02:27 PM
What are the differences between Huawei GT3 Pro and GT4?
Dec 29, 2023 pm 02:27 PM
Many users will choose the Huawei brand when choosing smart watches. Among them, Huawei GT3pro and GT4 are very popular choices. Many users are curious about the difference between Huawei GT3pro and GT4. Let’s introduce the two to you. . What are the differences between Huawei GT3pro and GT4? 1. Appearance GT4: 46mm and 41mm, the material is glass mirror + stainless steel body + high-resolution fiber back shell. GT3pro: 46.6mm and 42.9mm, the material is sapphire glass + titanium body/ceramic body + ceramic back shell 2. Healthy GT4: Using the latest Huawei Truseen5.5+ algorithm, the results will be more accurate. GT3pro: Added ECG electrocardiogram and blood vessel and safety
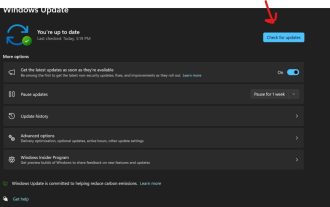 Fix: Snipping tool not working in Windows 11
Aug 24, 2023 am 09:48 AM
Fix: Snipping tool not working in Windows 11
Aug 24, 2023 am 09:48 AM
Why Snipping Tool Not Working on Windows 11 Understanding the root cause of the problem can help find the right solution. Here are the top reasons why the Snipping Tool might not be working properly: Focus Assistant is On: This prevents the Snipping Tool from opening. Corrupted application: If the snipping tool crashes on launch, it might be corrupted. Outdated graphics drivers: Incompatible drivers may interfere with the snipping tool. Interference from other applications: Other running applications may conflict with the Snipping Tool. Certificate has expired: An error during the upgrade process may cause this issu simple solution. These are suitable for most users and do not require any special technical knowledge. 1. Update Windows and Microsoft Store apps
 What does private mean in java
Nov 24, 2022 pm 06:27 PM
What does private mean in java
Nov 24, 2022 pm 06:27 PM
In Java, private means "private" and is an access control modifier used to modify classes, properties and methods. Class members modified with private can only be accessed and modified by the methods of the class itself, and cannot be accessed and referenced by any other class (including subclasses of the class); therefore, the private modifier has the highest level of protection.
 How to Fix Can't Connect to App Store Error on iPhone
Jul 29, 2023 am 08:22 AM
How to Fix Can't Connect to App Store Error on iPhone
Jul 29, 2023 am 08:22 AM
Part 1: Initial Troubleshooting Steps Checking Apple’s System Status: Before delving into complex solutions, let’s start with the basics. The problem may not lie with your device; Apple's servers may be down. Visit Apple's System Status page to see if the AppStore is working properly. If there's a problem, all you can do is wait for Apple to fix it. Check your internet connection: Make sure you have a stable internet connection as the "Unable to connect to AppStore" issue can sometimes be attributed to a poor connection. Try switching between Wi-Fi and mobile data or resetting network settings (General > Reset > Reset Network Settings > Settings). Update your iOS version:
 php提交表单通过后,弹出的对话框怎样在当前页弹出,该如何解决
Jun 13, 2016 am 10:23 AM
php提交表单通过后,弹出的对话框怎样在当前页弹出,该如何解决
Jun 13, 2016 am 10:23 AM
php提交表单通过后,弹出的对话框怎样在当前页弹出php提交表单通过后,弹出的对话框怎样在当前页弹出而不是在空白页弹出?想实现这样的效果:而不是空白页弹出:------解决方案--------------------如果你的验证用PHP在后端,那么就用Ajax;仅供参考:HTML code
 An article that understands this point and catches up with 70% of front-end people
Sep 06, 2022 pm 05:03 PM
An article that understands this point and catches up with 70% of front-end people
Sep 06, 2022 pm 05:03 PM
A colleague got stuck due to a bug pointed by this. Vue2’s this pointing problem caused an arrow function to be used, resulting in the inability to get the corresponding props. He didn't know it when I introduced it to him, and then I deliberately looked at the front-end communication group. So far, at least 70% of front-end programmers still don't understand it. Today I will share with you this link. If everything is wrong If you haven’t learned it yet, please give me a big mouth.
 Let's talk about why Vue2 can access properties in various options through this
Dec 08, 2022 pm 08:22 PM
Let's talk about why Vue2 can access properties in various options through this
Dec 08, 2022 pm 08:22 PM
This article will help you interpret the vue source code and introduce why you can use this to access properties in various options in Vue2. I hope it will be helpful to everyone!
 Detailed explanation of private access modifiers for Java functions
Apr 25, 2024 pm 04:48 PM
Detailed explanation of private access modifiers for Java functions
Apr 25, 2024 pm 04:48 PM
Private is a Java access modifier that limits the accessibility of a function to only the class in which it is defined, including: the function cannot be accessed in other classes. The function is also not accessible in subclasses.




