php实现Bloom Filter
Bloom Filter(BF) 是由Bloom在1970年提出的一种多哈希函数映射的快速查找算法,用于快速查找某个元素是否属于集合, 但不要求百分百的准确率。 Bloom filter通常用于爬虫的url去重,即判断某个url是否已经被爬过。 原理方面我引用一篇别人的文章,讲的比较清晰了,在此我不予赘述, 更多信息可以参考其论文。 看过几个php实现的BF,都觉得可读性不是很强, 本文主要给出我对Bloom Filter的一个php实现。
原理:
一. 实例
为了说明Bloom Filter存在的重要意义,举一个实例:
假设要你写一个网络蜘蛛(web crawler)。由于网络间的链接错综复杂,蜘蛛在网络间爬行很可能会形成“环”。为了避免形成“环”,就需要知道蜘蛛已经访问过那些URL。给一个URL,怎样知道蜘蛛是否已经访问过呢?稍微想想,就会有如下几种方案:
1. 将访问过的URL保存到数据库。
2. 用HashSet将访问过的URL保存起来。那只需接近O(1)的代价就可以查到一个URL是否被访问过了。
3. URL经过MD5或SHA-1等单向哈希后再保存到HashSet或数据库。
4. Bit-Map方法。建立一个BitSet,将每个URL经过一个哈希函数映射到某一位。
方法1~3都是将访问过的URL完整保存,方法4则只标记URL的一个映射位。
以上方法在数据量较小的情况下都能完美解决问题,但是当数据量变得非常庞大时问题就来了。
方法1的缺点:数据量变得非常庞大后关系型数据库查询的效率会变得很低。而且每来一个URL就启动一次数据库查询是不是太小题大做了?
方法2的缺点:太消耗内存。随着URL的增多,占用的内存会越来越多。就算只有1亿个URL,每个URL只算50个字符,就需要5GB内存。
方法3:由于字符串经过MD5处理后的信息摘要长度只有128Bit,SHA-1处理后也只有160Bit,因此方法3比方法2节省了好几倍的内存。
方法4消耗内存是相对较少的,但缺点是单一哈希函数发生冲突的概率太高。还记得数据结构课上学过的Hash表冲突的各种解决方法么?若要降低冲突发生的概率到1%,就要将BitSet的长度设置为URL个数的100倍。
实质上上面的算法都忽略了一个重要的隐含条件:允许小概率的出错,不一定要100%准确!也就是说少量url实际上没有没网络蜘蛛访问,而将它们错判为已访问的代价是很小的??大不了少抓几个网页呗。
二. Bloom Filter的算法
废话说到这里,下面引入本篇的主角??Bloom Filter。其实上面方法4的思想已经很接近Bloom Filter了。方法四的致命缺点是冲突概率高,为了降低冲突的概念,Bloom Filter使用了多个哈希函数,而不是一个。
Bloom Filter算法如下:
(1)初始化
创建一个m位BitSet,先将所有位初始化为0,然后选择k个不同的哈希函数。第i个哈希函数对字符串str哈希的结果记为h(i,str),且h(i,str)的范围是0到m-1 。
(2) 检查字符串是否存在
下面是检查字符串str是否被BitSet记录过的过程:
对于字符串str,分别计算h(1,str),h(2,str)…… h(k,str)。然后检查BitSet的第h(1,str)、h(2,str)…… h(k,str)位是否为1,若其中任何一位不为1则可以判定str一定没有被记录过。若全部位都是1,则“认为”字符串str存在。
若一个字符串对应的Bit不全为1,则可以肯定该字符串一定没有被Bloom Filter记录过。(这是显然的,因为字符串被记录过,其对应的二进制位肯定全部被设为1了)
但是若一个字符串对应的Bit全为1,实际上是不能100%的肯定该字符串被Bloom Filter记录过的。(因为有可能该字符串的所有位都刚好是被其他字符串所对应)这种将该字符串划分错的情况,称为false positive 。
(3) 删除字符串 :
字符串加入了就被不能删除了,因为删除会影响到其他字符串。实在需要删除字符串的可以使用Counting bloomfilter(CBF),这是一种基本Bloom Filter的变体,CBF将基本Bloom Filter每一个Bit改为一个计数器,这样就可以实现删除字符串的功能了。
Bloom Filter跟单哈希函数Bit-Map不同之处在于:Bloom Filter使用了k个哈希函数,每个字符串跟k个bit对应。从而降低了冲突的概率。
三. Bloom Filter参数选择
(1)哈希函数选择
哈希函数的选择对性能的影响应该是很大的,一个好的哈希函数要能近似等概率的将字符串映射到各个Bit。选择k个不同的哈希函数比较麻烦,一种简单的方法是选择一个哈希函数,然后送入k个不同的参数。
(2)Bit数组大小选择
哈希函数个数k、位数组大小m、加入的字符串数量n的关系可以参考参考文献1。该文献证明了对于给定的m、n,当 k = ln(2)* m/n 时出错的概率是最小的。
同时该文献还给出特定的k,m,n的出错概率。例如:根据参考文献,哈希函数个数k取10,位数组大小m设为字符串个数n的20倍时,false positive发生的概率是0.0000889 ,这个概率基本能满足网络爬虫的需求了。
实现:
<?php ///*************************************************************************** // * // * Copyright (c) 2015 Baidu.com, Inc. All Rights Reserved // * // **************************************************************************/ // // // ///** // * @file bloomfilter.php // * @author Rachel Zhang(zrqsophia@sina.com) // * @date 2015/07/24 18:48:57 // * @version $Revision$ // * @brief // * // **/ class BloomFilter{ var $m; # blocksize var $n; # number of strings to hash var $k; # number of hashing functions var $bitset; # hashing block with size m function BloomFilter($mInit,$nInit){ $this->m = $mInit; $this->n = $nInit; $this->k = ceil(($this->m/$this->n)*log(2)); echo "number of functions: $this->k\n"; $this->bitset = array_fill(0, $this->m, false); } function hashcode($str){ $res = array(); #put k hashing bit into $res $seed = crc32($str); mt_srand($seed); // set random seed, or mt_rand wouldn't provide same random arrays at different generation for($i=0 ; $i<$this->k ; $i++){ $res[] = mt_rand(0,$this->m-1); } return $res; } function addKey($key){ foreach($this->hashcode($key) as $codebit){ $this->bitset[$codebit]=true; } } function existKey($key){ $code=$this->hashcode($key); foreach($code as $codebit){ if($this->bitset[$codebit]==false){ return false; } } return true; } } $bf = new BloomFilter(10,2); $str_add1 = "test1"; $str_add2 = "test2"; $str_notadd3 = "test3"; //var_dump($bf->hashcode($str)); $bf->addKey($str_add1); $bf->addKey($str_add2); var_dump($bf->existKey($str_add1)); var_dump($bf->existKey($str_add2)); var_dump($bf->existKey($str_notadd3)); ?>
版权声明:本文为博主原创文章,未经博主允许不得转载。

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1376
1376
 52
52
 Working with Flash Session Data in Laravel
Mar 12, 2025 pm 05:08 PM
Working with Flash Session Data in Laravel
Mar 12, 2025 pm 05:08 PM
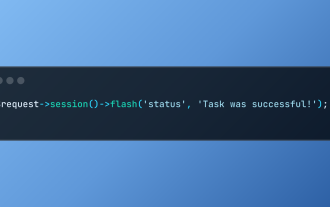
Laravel simplifies handling temporary session data using its intuitive flash methods. This is perfect for displaying brief messages, alerts, or notifications within your application. Data persists only for the subsequent request by default: $request-
 cURL in PHP: How to Use the PHP cURL Extension in REST APIs
Mar 14, 2025 am 11:42 AM
cURL in PHP: How to Use the PHP cURL Extension in REST APIs
Mar 14, 2025 am 11:42 AM
The PHP Client URL (cURL) extension is a powerful tool for developers, enabling seamless interaction with remote servers and REST APIs. By leveraging libcurl, a well-respected multi-protocol file transfer library, PHP cURL facilitates efficient execution of various network protocols, including HTTP, HTTPS, and FTP. This extension offers granular control over HTTP requests, supports multiple concurrent operations, and provides built-in security features.
 Alipay PHP SDK transfer error: How to solve the problem of 'Cannot declare class SignData'?
Apr 01, 2025 am 07:21 AM
Alipay PHP SDK transfer error: How to solve the problem of 'Cannot declare class SignData'?
Apr 01, 2025 am 07:21 AM
Alipay PHP...
 Simplified HTTP Response Mocking in Laravel Tests
Mar 12, 2025 pm 05:09 PM
Simplified HTTP Response Mocking in Laravel Tests
Mar 12, 2025 pm 05:09 PM
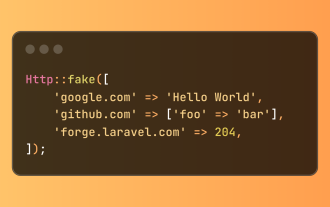
Laravel provides concise HTTP response simulation syntax, simplifying HTTP interaction testing. This approach significantly reduces code redundancy while making your test simulation more intuitive. The basic implementation provides a variety of response type shortcuts: use Illuminate\Support\Facades\Http; Http::fake([ 'google.com' => 'Hello World', 'github.com' => ['foo' => 'bar'], 'forge.laravel.com' =>
 12 Best PHP Chat Scripts on CodeCanyon
Mar 13, 2025 pm 12:08 PM
12 Best PHP Chat Scripts on CodeCanyon
Mar 13, 2025 pm 12:08 PM
Do you want to provide real-time, instant solutions to your customers' most pressing problems? Live chat lets you have real-time conversations with customers and resolve their problems instantly. It allows you to provide faster service to your custom
 Explain the concept of late static binding in PHP.
Mar 21, 2025 pm 01:33 PM
Explain the concept of late static binding in PHP.
Mar 21, 2025 pm 01:33 PM
Article discusses late static binding (LSB) in PHP, introduced in PHP 5.3, allowing runtime resolution of static method calls for more flexible inheritance.Main issue: LSB vs. traditional polymorphism; LSB's practical applications and potential perfo
 Customizing/Extending Frameworks: How to add custom functionality.
Mar 28, 2025 pm 05:12 PM
Customizing/Extending Frameworks: How to add custom functionality.
Mar 28, 2025 pm 05:12 PM
The article discusses adding custom functionality to frameworks, focusing on understanding architecture, identifying extension points, and best practices for integration and debugging.
 Framework Security Features: Protecting against vulnerabilities.
Mar 28, 2025 pm 05:11 PM
Framework Security Features: Protecting against vulnerabilities.
Mar 28, 2025 pm 05:11 PM
Article discusses essential security features in frameworks to protect against vulnerabilities, including input validation, authentication, and regular updates.




