 Backend Development
Backend Development
 PHP Tutorial
PHP Tutorial
 PHP calculates the distance based on the longitude and latitude between two points, PHP calculates the longitude and latitude of two points_PHP tutorial
PHP calculates the distance based on the longitude and latitude between two points, PHP calculates the longitude and latitude of two points_PHP tutorial
PHP calculates the distance based on the longitude and latitude between two points, PHP calculates the longitude and latitude of two points_PHP tutorial
PHP calculates the distance based on the longitude and latitude between two points, PHP calculates the longitude and latitude of two points
This is a good example. Paste the code directly. First you need to know the latitude and longitude values
/**
* @desc 根据两点间的经纬度计算距离
* @param float $lat 纬度值
* @param float $lng 经度值
*/
function getDistance($lat1, $lng1, $lat2, $lng2)
{
$earthRadius = 6367000; //approximate radius of earth in meters
/*
Convert these degrees to radians
to work with the formula
*/
$lat1 = ($lat1 * pi() ) / 180;
$lng1 = ($lng1 * pi() ) / 180;
$lat2 = ($lat2 * pi() ) / 180;
$lng2 = ($lng2 * pi() ) / 180;
/*
Using the
Haversine formula
http://en.wikipedia.org/wiki/Haversine_formula
calculate the distance
*/
$calcLongitude = $lng2 - $lng1;
$calcLatitude = $lat2 - $lat1;
$stepOne = pow(sin($calcLatitude / 2), 2) + cos($lat1) * cos($lat2) * pow(sin($calcLongitude / 2), 2);
$stepTwo = 2 * asin(min(1, sqrt($stepOne)));
$calculatedDistance = $earthRadius * $stepTwo;
return round($calculatedDistance);
}
I don’t know how to calculate this thing, but I found some problems in your code when I looked at the code.
First, the square of the straight-line distance between two points: $len is not used after the calculation, and there is no return. It is completely useless.
Second, enter the same longitude and latitude, and the result is not 0, and it is still a very large number, so there should be something wrong
You can use Baidu to calculate the distance between two points by "php" ”, there are a lot of ready-made codes
I think this introduction is more detailed, and there are codes, you can take a look
blog.csdn.net/...963740
Same latitude and different longitudes (except the equator)
h X 111 A triangle
For example, two points AB have different longitudes and latitudes (A longitude and B latitude)
Then first calculate the distance of the latitude B' that is collinear with point A, and then calculate the distance from A to B', then use The Pythagorean Theorem can be used to derive
Simply speaking, the following general formula can be used:
The distance formula between any two points on the earth:
The longitudes of any two points on the earth are A1 and A2 (E is positive , W negative), the latitudes are B1 and B2 (N positive, S negative) respectively.
Let A0=(A1-A2)÷2, B0=(BI-B2)÷2
f=√sinB0×sinB0+cosB1×cosB2×sinA0×sinA0
then
1. Straight-line distance in space between two points = 2fR
2. Minimum spherical distance between two points = arcsinf÷90°×∏R (angle)
3. Minimum spherical distance between two points = arcsinf×2R (radians)
Explanation: E, W, N, S = east, west, north, south; R = radius of the earth; √ = square root; ∏ = pi.
Put in the formula and do the calculation yourself
http://www.bkjia.com/PHPjc/904006.html

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1377
1377
 52
52
 C program to calculate distance between three points in 3D space
Aug 29, 2023 pm 12:41 PM
C program to calculate distance between three points in 3D space
Aug 29, 2023 pm 12:41 PM
Given a three-dimensional plane and therefore three coordinates, the task is to find the distance between the given points and display the result. On the three-dimensional plane, there are three coordinate axes, the coordinates of the x-axis are (x1, y1, z1), the coordinates of the y-axis are (x2, y2, z2), and the coordinates of the z-axis are (x3, y3, z). There is a direct formula for calculating the distance between them as follows $$\sqrt{\lgroupx2-x1\rgroup^{2}+\lgroupy2-y1\rgroup^{2}+\lgroupz2-z1\rgroup^{2 }}$$The following is an illustration showing three different coordinate axes and their coordinates. The method used below is as follows −Input coordinates (x1,
 Numerical distance based on machine learning: the distance between points in space
Apr 11, 2023 pm 11:40 PM
Numerical distance based on machine learning: the distance between points in space
Apr 11, 2023 pm 11:40 PM
This article is reprinted from the WeChat public account "Living in the Information Age". The author lives in the information age. To reprint this article, please contact the Living in the Information Age public account. In machine learning, a basic concept is how to judge the difference between two samples, so that the similarity and category information between the two samples can be evaluated. The measure to judge this similarity is the distance between two samples in the feature space. There are many measurement methods based on different data characteristics. Generally speaking, for two data samples x, y, define a function d(x, y). If it is defined as the distance between the two samples, then d(x, y) needs to satisfy the following basic properties : Non-negativity: d(x, y)>=0 Identity: d(x, y)=0 ⇔ x=y pair
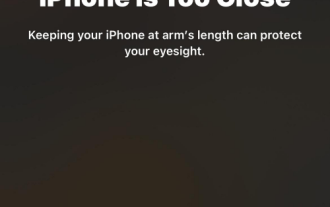 How to enable and use screen distance on iOS 17
Jun 29, 2023 pm 01:37 PM
How to enable and use screen distance on iOS 17
Jun 29, 2023 pm 01:37 PM
At its annual developers conference, Apple unveiled the next generation of operating systems to power its suite of devices. As usual, iOS 17 is at the center of all the major changes, with features like live voicemail, message transcription, live stickers, standby mode, full-screen live activities, interactive widgets, and more. One of the features that stands out among these new additions is Screen Distance. This is a health-centric feature focused on preventing eye strain and myopia on your iPhone screen. In this article, we will explain what screen distance is and how to enable it in iOS17. What is screen distance on iOS17? As part of the new health features introduced in iOS 17, Apple is offering a screen distance feature to help users anticipate
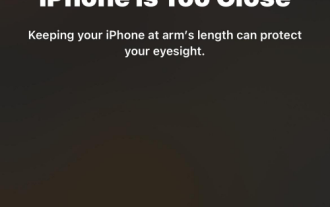 iOS 17: How to enable and use screen distance on iPhone
Sep 21, 2023 pm 02:25 PM
iOS 17: How to enable and use screen distance on iPhone
Sep 21, 2023 pm 02:25 PM
What is the screen distance feature in iOS17 update? Apple provides a screen distance function on the iPhone to help users prevent eye fatigue and the risk of myopia. The feature (available on iOS 17 or later) will use the iPhone's TrueDepth camera (the same camera that also helps FaceID) to measure the distance between the face and the phone. If Screen Distance detects that you are holding your iPhone closer than 12 inches or 30 centimeters for an extended period of time, it will prompt you to maintain distance from the iPhone screen. When your device detects that it is less than 12 inches from your face, you will see the "iPhone too close" message on the screen and advise that you should keep your distance to protect your vision. Only if you place the device further
 How to view longitude and latitude on Baidu Maps How to view longitude and latitude
Mar 12, 2024 pm 12:10 PM
How to view longitude and latitude on Baidu Maps How to view longitude and latitude
Mar 12, 2024 pm 12:10 PM
When we use this platform, we all know that every location has coordinates. I believe that students who have studied geography will know what the longitude and latitude coordinates are. The above functions can be said to be very powerful. Not only can you locate some of your locations in real time, but it can also let you know what the current longitude and latitude are. That is to say, we can all check the longitude and latitude coordinates of any location on the map. In this way, we can know the corresponding specific locations more accurately, but the majority of users who don’t know are still viewing it, so in order to give you a better understanding of it, let’s join the editor now Take a look, I believe you won’t miss it, come and take a look.
 How to check latitude and longitude on Google Maps
Mar 24, 2024 pm 05:31 PM
How to check latitude and longitude on Google Maps
Mar 24, 2024 pm 05:31 PM
You can check the latitude and longitude on Google Maps, but how do you check the latitude and longitude? Users click on the information of a location, and then click to view more, to view the specific longitude and latitude information. This introduction to the method of checking longitude and latitude can tell you the specific content. The following is the detailed method, so take a look. How to check latitude and longitude on Google Maps A: Click on the location and select to view detailed information. Detailed introduction: Mobile version: 1. First, go to the progress map and select a location you want to view. 2. Click the View All button inside. 3. You can see the detailed latitude and longitude. PC version: 1. First enter the Google Maps website. https://www.google.cn2. Right-click to view the desired location and click What's here.
 The reason why the working distance of UWB base stations continues to increase - IOTE Internet of Things Exhibition
Nov 27, 2023 pm 01:21 PM
The reason why the working distance of UWB base stations continues to increase - IOTE Internet of Things Exhibition
Nov 27, 2023 pm 01:21 PM
An interesting trend has emerged for UWB technology in the industry application market: the transmission distance of base stations is gradually increasing. A typical scene is a tunnel or a mine. The characteristic of this scene is that the space is linear and there are not many obstructions in the middle. UWB Base stations are also laid out in straight lines. The farther the working distance of the base station, the fewer the number of base stations required for the project, and the lower the project cost. Under market competition, the working distance of UWB base stations on the market is getting farther and farther. The working distance of the base station has increased from tens of thousands in the early days. meters, expanded to 100m, 200m, 500m, 1000m, 2000m or even further. This article will not discuss the business logic behind this too much. Why do UWB base stations work farther and farther away? There are two key components, one is the antenna, and the other
 How to use Java code to display the latitude and longitude of the current location on Baidu Map?
Aug 06, 2023 pm 08:48 PM
How to use Java code to display the latitude and longitude of the current location on Baidu Map?
Aug 06, 2023 pm 08:48 PM
How to use Java code to display the latitude and longitude of the current location on Baidu Map? Baidu Maps is a very popular map application that is often used when developing geolocation-related applications. This article will introduce how to use Java code to display the longitude and latitude of the current location on Baidu Map. First, we need to prepare a Baidu developer account and create an application to obtain the API key. After registering an account and logging in on the Baidu developer website, we can create an application in the console and obtain an API key for accessing



