Detailed explanation of user rights_PHP tutorial
Read it if you have the patience (the algorithm is still important)
User initial weight: Enable = 0;
If a user has the first power Select, then the user weight: Enable = Enable + 1;
If If a user has the second power Insert, then the user weight is: Enable = Enable + 2;
If a user has the third power Update, then the user weight is: Enable = Enable + 4;
If a user If there is a fourth power, Delete, then the user weight is: Enable = Enable + 8;
Why +1, +2, +4, +8 in order, instead of +1, +2, +3, +4?
If it is +1, +2, +3, +4:
If a user has the first right Select, then the user weight is: Enable = Enable + 1;
If a user has the second If a user has the third right, Insert, then the user’s weight is: Enable = Enable + 2;
If a user has the third right, Update, then the user’s weight is: Enable = Enable + 3;
If a user has the fourth right, Update Delete, then the user weight is: Enable = Enable + 4;
Then when the user weight is: Enable = 3, you cannot judge whether the user has both the
first power Select and the second power Insert. Two rights, or only the third power, Update,
The former weight algorithm can avoid this situation.
But when using the former weight algorithm, how to quickly know which rights the user has
from the user's weight Enable? If the user rights value is Enable = 5, the user has the first power Select and the third power Update.
Note that the user does not have the second power Insert.
I will list the user rights below:
Power Possess Power User's weight Enable
SelectItem: (1, 3, 5, 7, 9, 11, 13, 15)
InsertItem: (2 , 3, 6, 7, 10, 11, 14, 15 )
UpdateItem: ( 4, 5, 6, 7, 12, 13, 14, 15 )
DeleteItem: (8, 9, 10, 11, 12, 13, 14, 15)
It can be seen that users with large Enable weights do not have "more" rights.
If: User Rights Value Enable = 3, the user has the first power (Select) and the second power (Insert), a total of two rights,
User power value Enable = 4, the user has the third power (Update), only one rights.
Look carefully at the "User Power List":
SelectItem: (1, 3, 5, 7, 9, 11, 13, 15): 1 = 0 + 2 raised to the 0th power; 3 = 2 raised to the 1st power Power + 2 to the 0th power; 5 = 2 to the 2nd power + 2 to the 0th power;
InsertItem: (2, 3, 6, 7, 10, 11, 14, 15): 2 = 0 + 2 1 power; 3 = 2 power 0 + 2 power 1; 6 = 2 power 2 + 2 power 1;
UpdateItem: (4, 5, 6, 7, 12, 13 , 14, 15): 4 = 0 + 2 to the power of 2; 5 = 2 to the power of 0 + 2 to the power of 2; 6 = 2 to the power of 2 + 2 to the power of 2;
DeleteItem: ( 8, 9, 10, 11, 12, 13, 14, 15): 8 = 0 + 2 to the 3rd power; 9 = 2 to the 0th power + 2 to the 3rd power 10 = 2 to the 1st power + 2 3rd power;
The rules are summarized as follows:
The weight of the Select user with the first power: Enable = ? + 2 to the 0th power; (where ? must also be divided into 2 and the Nth power added together Situation)
Have the second power Insert user's weight: Enable = ? + 1 power of 2; (where ? must also be split into the sum of N powers of 2)
Have the third power Power Update user’s weight: Enable = ? + 2 to the power of 2; (where ? must also be split into the sum of N powers of 2)
The fourth power of Delete user’s weight: Enable = ? + 2 to the 3rd power; (where ? must also be split into the sum of 2 to the Nth power)
It is already very clear at this point:
As long as the user's weight Enable is split into 2 to N In the case of summation of powers,
if there is N=0 in it, it has the first power Select,
if there is N=1 in it, it has the second power Insert,
if there is N in it =2, then you have the third power Update,
If N=3, you have the fourth power Delete,
Then how to quickly split the user weight Enable into the sum of N powers of 2 What's the situation?
Haha! Just convert Enable into binary and take the base from right to left. If the base is the bit, it has the corresponding rights.
For example:
(11)10=(1011)2, that is, it has the first, second, and The four powers are consistent with the "User Power List";
(12)10=(1100)2, that is, having the third and fourth powers, consistent with the "User Power List";
(15)10= (1111)2, that is, possessing the first, second, third, and fourth powers, consistent with the "user power list";
When the power level is extremely complex, the algorithm can quickly know the user's power:
For example:
A total of 8 levels, user weight Enable=67; (67)10=(1000011)2, that is, it has the first, sixth, and seventh powers,
User weight Enable=67; (159)10 =(10011111)2, that is, it has the first, fourth, fifth, sixth, seventh and eighth powers.
That’s it. I hope I didn’t waste your time and inspired you.

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 How to use Xiaohongshu account to find users? Can I find my mobile phone number?
Mar 22, 2024 am 08:40 AM
How to use Xiaohongshu account to find users? Can I find my mobile phone number?
Mar 22, 2024 am 08:40 AM
With the rapid development of social media, Xiaohongshu has become one of the most popular social platforms. Users can create a Xiaohongshu account to show their personal identity and communicate and interact with other users. If you need to find a user’s Xiaohongshu number, you can follow these simple steps. 1. How to use Xiaohongshu account to find users? 1. Open the Xiaohongshu APP, click the "Discover" button in the lower right corner, and then select the "Notes" option. 2. In the note list, find the note posted by the user you want to find. Click to enter the note details page. 3. On the note details page, click the "Follow" button below the user's avatar to enter the user's personal homepage. 4. In the upper right corner of the user's personal homepage, click the three-dot button and select "Personal Information"
 Log in to Ubuntu as superuser
Mar 20, 2024 am 10:55 AM
Log in to Ubuntu as superuser
Mar 20, 2024 am 10:55 AM
In Ubuntu systems, the root user is usually disabled. To activate the root user, you can use the passwd command to set a password and then use the su- command to log in as root. The root user is a user with unrestricted system administrative rights. He has permissions to access and modify files, user management, software installation and removal, and system configuration changes. There are obvious differences between the root user and ordinary users. The root user has the highest authority and broader control rights in the system. The root user can execute important system commands and edit system files, which ordinary users cannot do. In this guide, I'll explore the Ubuntu root user, how to log in as root, and how it differs from a normal user. Notice
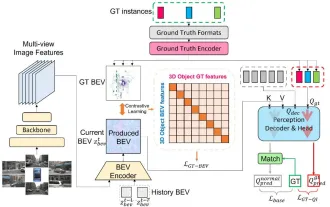 CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
Written above & the author’s personal understanding: At present, in the entire autonomous driving system, the perception module plays a vital role. The autonomous vehicle driving on the road can only obtain accurate perception results through the perception module. The downstream regulation and control module in the autonomous driving system makes timely and correct judgments and behavioral decisions. Currently, cars with autonomous driving functions are usually equipped with a variety of data information sensors including surround-view camera sensors, lidar sensors, and millimeter-wave radar sensors to collect information in different modalities to achieve accurate perception tasks. The BEV perception algorithm based on pure vision is favored by the industry because of its low hardware cost and easy deployment, and its output results can be easily applied to various downstream tasks.
 Detailed explanation of obtaining administrator rights in Win11
Mar 08, 2024 pm 03:06 PM
Detailed explanation of obtaining administrator rights in Win11
Mar 08, 2024 pm 03:06 PM
Windows operating system is one of the most popular operating systems in the world, and its new version Win11 has attracted much attention. In the Win11 system, obtaining administrator rights is an important operation. Administrator rights allow users to perform more operations and settings on the system. This article will introduce in detail how to obtain administrator permissions in Win11 system and how to effectively manage permissions. In the Win11 system, administrator rights are divided into two types: local administrator and domain administrator. A local administrator has full administrative rights to the local computer
 Detailed explanation of division operation in Oracle SQL
Mar 10, 2024 am 09:51 AM
Detailed explanation of division operation in Oracle SQL
Mar 10, 2024 am 09:51 AM
Detailed explanation of division operation in OracleSQL In OracleSQL, division operation is a common and important mathematical operation, used to calculate the result of dividing two numbers. Division is often used in database queries, so understanding the division operation and its usage in OracleSQL is one of the essential skills for database developers. This article will discuss the relevant knowledge of division operations in OracleSQL in detail and provide specific code examples for readers' reference. 1. Division operation in OracleSQL
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Analysis of user password storage mechanism in Linux system
Mar 20, 2024 pm 04:27 PM
Analysis of user password storage mechanism in Linux system
Mar 20, 2024 pm 04:27 PM
Analysis of user password storage mechanism in Linux system In Linux system, the storage of user password is one of the very important security mechanisms. This article will analyze the storage mechanism of user passwords in Linux systems, including the encrypted storage of passwords, the password verification process, and how to securely manage user passwords. At the same time, specific code examples will be used to demonstrate the actual operation process of password storage. 1. Encrypted storage of passwords In Linux systems, user passwords are not stored in the system in plain text, but are encrypted and stored. L
 Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
The bottom layer of the C++sort function uses merge sort, its complexity is O(nlogn), and provides different sorting algorithm choices, including quick sort, heap sort and stable sort.






