js basic algorithm: bubble sort, binary search

Knowledge expansion:

Time complexity: The time complexity of an algorithm is a function that describes the running time of the algorithm. The lower the time complexity, the higher the efficiency.

Self-understanding: The time complexity of an algorithm will be determined by running it several times. If it is run n times, the time complexity will be O(n).

1. Bubble sort

Analysis: 1. Compare two adjacent elements. If the former one is larger than the latter one, swap positions.

　　2. In the first round, the last element should be the largest one.

　 3. Compare two adjacent elements according to step 1. At this time, since the last element is already the largest, there is no need to compare the last element.

　　

function sort(elements){
 for(var i=0;i<elements.length-1;i++){
  for(var j=0;j<elements.length-i-1;j++){
   if(elements[j]>elements[j+1]){
    var swap=elements[j];
    elements[j]=elements[j+1];
    elements[j+1]=swap;
   }
  }
 }
}
 
var elements = [3, 1, 5, 7, 2, 4, 9, 6, 10, 8];
console.log(&#39;before: &#39; + elements);
sort(elements);
console.log(&#39; after: &#39; + elements);

2. Quick sort

Analysis: Quick sort is an improvement on bubble sort. In the first sorting pass, the data is divided into two parts, one part is smaller than all the data in the other part. Then call it recursively, performing quick sort on both sides.

function  quickSort(elements) {
 
　　if (elements.length <= 1) { return elements; }
 
    var pivotIndex = Math.floor(elements.length / 2);
 
    var pivot = elements.splice(pivotIndex, 1)[0];
 
 
　　var left = [];
 
　　var right = [];
 
　　for (var i = 0; i < elements.length; i++){
 
　　　　if (elements[i] < pivot) {
 
　　　　　　left.push(elements[i]);
 
　　　　} else {
 
　　　　　　right.push(elements[i]);
 
　　　　}
 
　　}
 
　　return quickSort(left).concat([pivot], quickSort(right));
 
};
 
var elements=[5,6,2,1,3,8,7,1.2,5.5,4.5];
alert(quickSort(elements));

3. Insertion sort

Analysis:

(1) Starting from the first element, the element can be considered to have been sorted

(2) Take out the next element and proceed from backward in the sorted element sequence Front scan

(3) If the element (sorted) is greater than the new element, move the element to the next position

(4) Repeat step 3 until you find the position where the sorted element is less than or equal to the new element

(5) Insert the new element into the next position

(6) Repeat step 2

insertSort: function(elements) {

    var i = 1,
    j, step, key, len = elements.length;

    for (; i < len; i++) {

        step = j = i;
        key = elements[j];

        while (--j > -1) {
            if (elements[j] > key) {
                elements[j + 1] = elements[j];
            } else {
                break;
            }
        }

        elements[j + 1] = key;
    }

    return elements;
}

2. Binary search

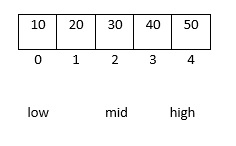
Analysis: Binary search, also a binary search. First, find a middle value. By comparing it with the middle value, the larger one is placed and the smaller one is placed on the left. Then find the middle value on both sides and continue the above operation until you find the location.

(1) Recursive method

function binarySearch(data,item,start,end){
    var end=end || data.length-1;
    var start=start || 0;
    var m=Math.floor((start+end)/2);
    if(item==data[m]){
        return m;
    }else if(item<data[m]){
        return binarySearch(data,item,start,m-1) //递归调用
    }else{
        return binarySearch(data,item,m+1,end);
    }
    return false;
}

    var arr=[34,12,5,123,2,745,32,4];

    binary(arr,5);

(2) Non-recursive method

function binarySearch(data, item){
    var h = data.length - 1,
        l = 0;
    while(l <= h){
        var m = Math.floor((h + l) / 2);
        if(data[m] == item){
            return m;
        }
        if(item > data[m]){
            l = m + 1;
        }else{
            h = m - 1;
        }
    }
  
    return false;
}
var arr=[34,12,5,123,2,745,32,4];
binarySearch(arr,5);