Background
Quick sort is a sorting method proposed by American Tony Hall in the 1960s. This sorting method was already a very fast sorting method at the time. Therefore, in terms of naming, it is called "quick sort". This algorithm is one of the seven major algorithms of the 20th century. The average time complexity is Ο(nlogn), and in the case of O(nlogn), the actual operation speed is faster than other sorting with the same time complexity. method.
Students who are interested in Tony Hall and the background of quick sorting can check out this introduction: http://www.nowamagic.net/librarys/veda/detail/2391
Sorting Thoughts
Quick The idea of sorting is difficult to think of, but it is very easy to understand. His idea is as follows:
1. First select a certain element in the queue as the base value (generally select the head element or tail element).
2. Compare the base Value with all elements in sequence. The elements are divided into two queues A and B according to the comparison results. One with all elements greater than the base Value, and one with all elements smaller than the base Value.
3. Use A as a new queue, select the base again, and then divide it into two smaller queues.
4. In this way, continue to split each small queue into two smaller queues indefinitely.
5. Until a queue has been split into pieces that cannot be unpacked (that is, one element)
6. Because the order between queues is fixed. Combine these queues at once, and the overall sorting is completed.
(Anti-theft connection: This article was first published from http://www.cnblogs.com/jilodream/ )
Note that there are two core steps here, which are
1. Select the Value element and divide the entire queue into two Sub-queue
2. Then re-use the sub-queue as a new queue with an overall size smaller than the current one, and perform calculations until the calculation is very easy.
These two core steps create the inherent advantages of quick sort:
1. By comparing the size of the elements divided into subqueues, in the future comparison process, the comparison range of this element will always stay in this subqueue. , no more unnecessary comparisons will be made. This allows early comparisons to still have a strong impact on later comparisons. Similar to the bubble sorting method, many comparisons in the early stage have very little effect in the later stage. This is very similar to the kmp algorithm. The early comparison should try to make maximum use.
2. Split the original scale queue into several small sub-queues. These sub-queues need to solve the same problems as (anti-theft connection: this article was first published at http://www.cnblogs.com/jilodream/) The original queue is the same, but the size is smaller. Such constant division creates a divide-and-conquer mentality. This idea also coincides with the backpack algorithm.
For students who have difficulty understanding text, you can take a look at the classic online dynamic picture below, which is very vivid:
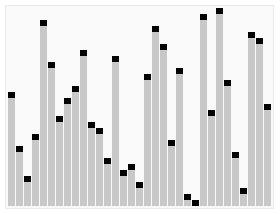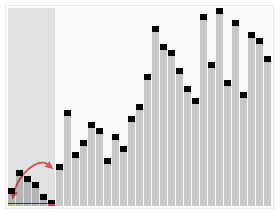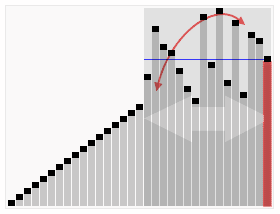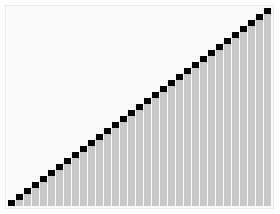 The following is the code implemented in java
The following is the code implemented in java
import java.util.Arrays;
public class QuickSort
{
public static void main(String args[])
{
QuickSort quicksort = new QuickSort();
int[] arrays = new int[]
{ 1, 12, 2, 13, 3, 14, 4, 15, 5, 16, 17, 17, 177, 18, 8, 8, 19 };
quicksort.quickSort(arrays);
System.out.println(Arrays.toString(arrays));
}
private void quickSort(int[] arrays)
{
subQuickSort(arrays, 0, arrays.length - 1);
}
private void subQuickSort(int[] arrays, int start, int end)
{
if (start >= end)
{
return;
}
int middleIndex = subQuickSortCore(arrays, start, end);
subQuickSort(arrays, start, middleIndex - 1);
subQuickSort(arrays, middleIndex + 1, end);
}
private int subQuickSortCore(int[] arrays, int start, int end)
{
int middleValue = arrays[start];
while (start < end)
{
while (arrays[end] >= middleValue && start < end)
{
end--;
}
arrays[start] = arrays[end];
while (arrays[start] <= middleValue && start < end)
{
start++;
}
arrays[end] = arrays[start];
}
arrays[start] = middleValue;
return start;
}
}



