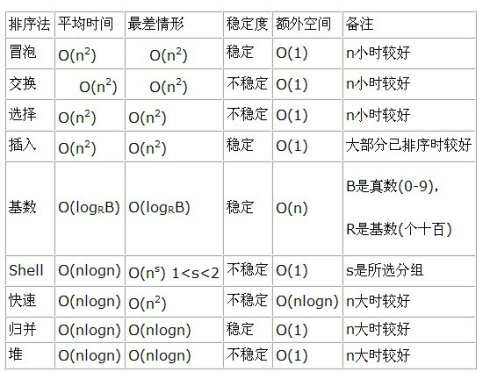
A summary of common centralized sorting algorithms
Merge sort
Merge sort, also called merge sort, is a typical application of the divide-and-conquer method. The idea of divide and conquer is to decompose each problem into small problems, solve each small problem, and then merge them.
The specific merge sort is to recursively decompose a set of unordered numbers into sub-items with only one element by n/2, and one element is already sorted. Then merge these ordered sub-elements.
The process of merging is to compare two sorted subsequences, first select the smallest element in the two subsequences, select the smallest subsequence of the two elements, and remove and add it from the subsequence
to the final result set until the two subsequences are merged.
The code is as follows:
#!/usr/bin/python
import sys
def merge(nums, first, middle, last):
''''' merge '''
# 切片边界,左闭右开并且是了0为开始
lnums = nums[first:middle+1]
rnums = nums[middle+1:last+1]
lnums.append(sys.maxint)
rnums.append(sys.maxint)
l = 0
r = 0
for i in range(first, last+1):
if lnums[l] < rnums[r]:
nums[i] = lnums[l]
l+=1
else:
nums[i] = rnums[r]
r+=1
def merge_sort(nums, first, last):
''''' merge sort
merge_sort函数中传递的是下标，不是元素个数
'''
if first < last:
middle = (first + last)/2
merge_sort(nums, first, middle)
merge_sort(nums, middle+1, last)
merge(nums, first, middle,last)
if __name__ == '__main__':
nums = [10,8,4,-1,2,6,7,3]
print 'nums is:', nums
merge_sort(nums, 0, 7)
print 'merge sort:', nums
Stable, time complexity O(nlog n)
Insertion sort
The code is as follows:
#!/usr/bin/python
import sys
def insert_sort(a):
''''' 插入排序
有一个已经有序的数据序列，要求在这个已经排好的数据序列中插入一个数，
但要求插入后此数据序列仍然有序。刚开始 一个元素显然有序，然后插入一
个元素到适当位置，然后再插入第三个元素，依次类推
'''
a_len = len(a)
if a_len = 0 and a[j] > key:
a[j+1] = a[j]
j-=1
a[j+1] = key
return a
if __name__ == '__main__':
nums = [10,8,4,-1,2,6,7,3]
print 'nums is:', nums
insert_sort(nums)
print 'insert sort:', nums
Stable, time complexity O(n^2)
To exchange the values of two elements in python, you can write: a, b = b, a. In fact, this is because the left and right sides of the assignment symbol are tuples
(It needs to be emphasized here that in python, tuples In fact, it is delimited by commas "," instead of brackets).
Selection sort
Selection sort is a simple and intuitive sorting algorithm. Here's how it works. First, find the smallest (large) element in the unsorted sequence and store it at the beginning of the sorted sequence. Then, continue to find the smallest (large) element from the remaining unsorted elements, and then put it at the end of the sorted sequence. And so on, until all elements are sorted.
import sys
def select_sort(a):
''''' 选择排序
每一趟从待排序的数据元素中选出最小（或最大）的一个元素，
顺序放在已排好序的数列的最后，直到全部待排序的数据元素排完。
选择排序是不稳定的排序方法。
'''
a_len=len(a)
for i in range(a_len):#在0-n-1上依次选择相应大小的元素
min_index = i#记录最小元素的下标
for j in range(i+1, a_len):#查找最小值
if(a[j]<a[min_index]):
min_index=j
if min_index != i:#找到最小元素进行交换
a[i],a[min_index] = a[min_index],a[i]
if __name__ == '__main__':
A = [10, -3, 5, 7, 1, 3, 7]
print 'Before sort:',A
select_sort(A)
print 'After sort:',A
Unstable, time complexity O(n^2)
Hill sorting
Hill sorting, also called descending incremental sorting algorithm, Hill sorting is a non-stable sorting algorithm. This method is also called reducing incremental sorting, because DL. Shell was named after it was proposed in 1959.
First take an integer d1 less than n as the first increment, and divide all records in the file into d1 groups. All records whose distance is a multiple of d1 are placed in the same group. First sort within each group;
Then, take the second increment d2 Unstable, time complexity average time O(nlogn) worst time O(n^s)1 Heap Sort (Heap Sort) The definition of "heap": in In the "heap" with a starting index of 0: The right child node of node i is at position 2 * i + 24) The parent node of node i is at position floor( (i - 1) / 2) : Note that floor means "take "Full" operation Characteristics of the heap: The key value of each node must always be greater than (or less than) its parent node "Max Heap": The root node of the "heap" saves the maximum key value node. That is, the key value of each node in the "heap" is always greater than its child nodes. Move up, move down: When the key value of a node is greater than its parent node, then we have to perform a "move up" operation, that is, we move the node to the position of its parent node, Let its parent node move to its position, and then we continue to judge the node and do not stop "moving up" until the node is no longer larger than its parent node. Now let’s learn more about the “move down” operation. When we change the key value of a node to a smaller value, we need to "move it down". Method: We first build a maximum heap (time complexity O(n)), and then each time we only need to exchange the root node with the node at the last position, and then exclude the last position, and then After the exchange, the heap of the root node is adjusted (time complexity O(lgn)), that is, the root node can be "moved down". The total time complexity of heap sort is O(nlgn). The code is as follows: Unstable, time complexity O(nlog n) Quick sort Quick sort algorithm and merge sort algorithm Likewise, it is also based on the divide-and-conquer model. The three steps of the divide-and-conquer process of quick sorting the subarray A[p...r] are: Decomposition: Divide the array A[p...r] into A[p...q-1] and A[q+1...r] two parts, where each element in A[p...q-1] is less than or equal to A[q] and each element in A[q+1...r] elements are greater than or equal to A[q]; Solution: Sort the subarrays A[p...q-1] and A[q+1...r] by recursively calling quick sort; Merge : Because the two subarrays are sorted in place, no additional operations are required. For the beginning of each iteration of partition partition, x=A[r], for any array subscript k, there are: 1) If p≤k≤i, then A[k]≤x. 2) If i+1≤k≤j-1, then A[k]>x. 3) If k=r, then A[k]=x. The code is as follows: Unstable, the best time complexity is O(nlogn) and the worst time is O(n^2) Let’s talk about sequences in python: Lists, tuples and strings are all sequences, but what are sequences? Why is it so special? The two main features of sequences are the indexing operator and the slicing operator. The index operator allows us to grab a specific item from a sequence. The slice operator allows us to obtain a slice of the sequence, that is, a part of the sequence, such as: a = ['aa','bb','cc'], print a[0] is an index operation, print a[0:2] for slicing operations. import sys
def shell_sort(a):
''''' shell排序
'''
a_len=len(a)
gap=a_len/2#增量
while gap>0:
for i in range(a_len):#对同一个组进行选择排序
m=i
j=i+1
while j<a_len:
if a[j]<a[m]:
m=j
j+=gap#j增加gap
if m!=i:
a[m],a[i]=a[i],a[m]
gap/=2
if __name__ == '__main__':
A = [10, -3, 5, 7, 1, 3, 7]
print 'Before sort:',A
shell_sort(A)
print 'After sort:',A#!/usr/bin env python
# 数组编号从 0开始
def left(i):
return 2*i +1
def right(i):
return 2*i+2
#保持最大堆性质 使以i为根的子树成为最大堆
def max_heapify(A, i, heap_size):
if heap_size <= 0:
return
l = left(i)
r = right(i)
largest = i # 选出子节点中较大的节点
if l A[largest]:
largest = l
if r A[largest]:
largest = r
if i != largest :#说明当前节点不是最大的，下移
A[i], A[largest] = A[largest], A[i] #交换
max_heapify(A, largest, heap_size)#继续追踪下移的点
#print A
# 建堆
def bulid_max_heap(A):
heap_size = len(A)
if heap_size >1:
node = heap_size/2 -1
while node >= 0:
max_heapify(A, node, heap_size)
node -=1
# 堆排序 下标从0开始
def heap_sort(A):
bulid_max_heap(A)
heap_size = len(A)
i = heap_size - 1
while i > 0 :
A[0],A[i] = A[i], A[0] # 堆中的最大值存入数组适当的位置，并且进行交换
heap_size -=1 # heap 大小 递减 1
i -= 1 # 存放堆中最大值的下标递减 1
max_heapify(A, 0, heap_size)
if __name__ == '__main__' :
A = [10, -3, 5, 7, 1, 3, 7]
print 'Before sort:',A
heap_sort(A)
print 'After sort:',A#!/usr/bin/env python
# 快速排序
'''''
划分 使满足 以A[r]为基准对数组进行一个划分，比A[r]小的放在左边，
比A[r]大的放在右边
快速排序的分治partition过程有两种方法，
一种是上面所述的两个指针索引一前一后逐步向后扫描的方法,
另一种方法是两个指针从首位向中间扫描的方法。
'''
#p,r 是数组A的下标
def partition1(A, p ,r):
'''''
方法一，两个指针索引一前一后逐步向后扫描的方法
'''
x = A[r]
i = p-1
j = p
while j < r:
if A[j] < x:
i +=1
A[i], A[j] = A[j], A[i]
j += 1
A[i+1], A[r] = A[r], A[i+1]
return i+1
def partition2(A, p, r):
'''''
两个指针从首尾向中间扫描的方法
'''
i = p
j = r
x = A[p]
while i = x and i < j:
j -=1
A[i] = A[j]
while A[i]<=x and i < j:
i +=1
A[j] = A[i]
A[i] = x
return i
# quick sort
def quick_sort(A, p, r):
'''''
快速排序的最差时间复杂度为O(n2)，平时时间复杂度为O(nlgn)
'''
if p < r:
q = partition2(A, p, r)
quick_sort(A, p, q-1)
quick_sort(A, q+1, r)
if __name__ == '__main__':
A = [5,-4,6,3,7,11,1,2]
print 'Before sort:',A
quick_sort(A, 0, 7)
print 'After sort:',A
![[Web front-end] Node.js quick start](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
