Calculate the value of π using Python
π is a truly magical number followed by countless people. I'm not quite sure what's so fascinating about an irrational number that repeats itself forever. In my opinion, I enjoy calculating π, that is, calculating the value of π. Because π is an irrational number, it is infinite. This means that any calculation of π is only an approximation. If you calculate 100 digits, I can calculate 101 digits and be more precise. So far, some have singled out supercomputers to try to calculate the most accurate π. Some extreme values include calculating 500 million digits of pi. You can even find a text file online containing 10 billion digits of π (be careful! This file may take a while to download, and it won't open with your usual Notepad application.). For me, how to calculate π with a few simple lines of Python is what interests me.

You can always use the math.pi variable. It is included in the standard library and you should use it before trying to calculate it yourself. In fact, we will use it to calculate accuracy. To start, let's look at a very straightforward method of calculating Pi. As usual, I'll be using Python 2.7, the same ideas and code may apply to different versions. Most of the algorithms we will use are taken from and implemented on the Pi WikiPedia page. Let’s take a look at the code below:
importsys
importmath
defmain(argv):
iflen(argv) !=1:
sys.exit('Usage: calc_pi.py <n>')
print'\nComputing Pi v.01\n'
a=1.0
b=1.0/math.sqrt(2)
t=1.0/4.0
p=1.0
foriinrange(int(sys.argv[1])):
at=(a+b)/2
bt=math.sqrt(a*b)
tt=t-p*(a-at)**2
pt=2*p
a=at;b=bt;t=tt;p=pt
my_pi=(a+b)**2/(4*t)
accuracy=100*(math.pi-my_pi)/my_pi
print"Pi is approximately: "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if__name__=="__main__":
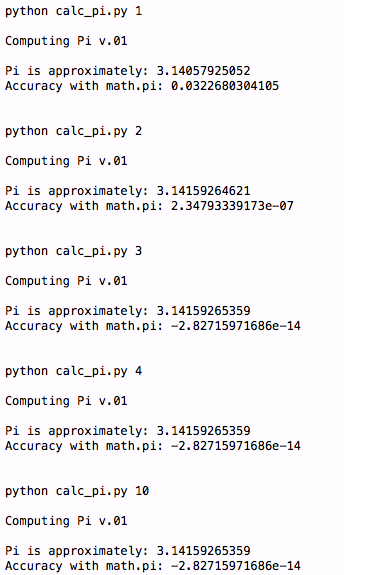
main(sys.argv[1:])This is a very simple script that you can download, run, modify, and share with others as you like. You can see output similar to the following:

You will find that even though n is greater than 4, the accuracy of our approximation to Pi does not improve much. We can guess that even if the value of n is larger, the same thing (the approximation accuracy of pi is not improved) will still happen. Luckily, there's more than one way to solve this mystery. Using the Python Decimal (decimal) library, we can get higher-precision values to approximate Pi. Let's see how the library functions are used. This simplified version can get numbers with more than 11 digits usually less precision than given by Python floating point numbers. Here's an example from the Python Decimal library:

See these numbers. wrong! We only entered 3.14, why did we get some junk? This is memory junk. In a nutshell, Python gives you the decimal number you want, plus a little extra value. It does not affect any calculations as long as the accuracy is less than the previous junk number at the beginning. You can specify how many digits you want by setting getcontext().prec. Let's try.
Very good. Now let's try using this to see if we can get a better approximation to our previous code. Now, I'm usually against using " from library import * ", but in this case it makes the code look prettier.
importsys
importmath
fromdecimalimport*
defmain(argv):
iflen(argv) !=1:
sys.exit('Usage: calc_pi.py <n>')
print'\nComputing Pi v.01\n'
a=Decimal(1.0)
b=Decimal(1.0/math.sqrt(2))
t=Decimal(1.0)/Decimal(4.0)
p=Decimal(1.0)
foriinrange(int(sys.argv[1])):
at=Decimal((a+b)/2)
bt=Decimal(math.sqrt(a*b))
tt=Decimal(t-p*(a-at)**2)
pt=Decimal(2*p)
a=at;b=bt;t=tt;p=pt
my_pi=(a+b)**2/(4*t)
accuracy=100*(Decimal(math.pi)-my_pi)/my_pi
print"Pi is approximately: "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if__name__=="__main__":
main(sys.argv[1:])Output result:
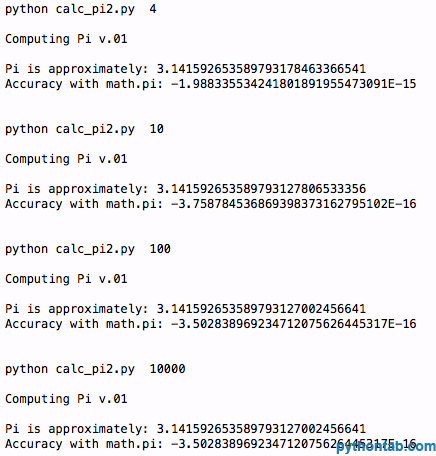
Okay. We're more accurate, but it looks like there's some rounding. From n = 100 and n = 1000, we have the same accuracy. What should we do now? Okay, now let's turn to formulas. So far, the way we've calculated Pi is by adding its parts together. I found some code from DAN's article on Calculating Pi. He suggested that we use the following 3 formulas:
Bailey–Borwein–Plouffe formula
Bellard’s formula
Chudnovsky algorithm
Let’s start with the Bailey–Borwein–Plouffe formula. It looks like this:
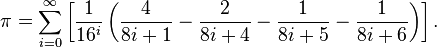
In code we can write it like this:
import sys
import math
from decimal import *
def bbp(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(1)/(16**k))*((Decimal(4)/(8*k+1))-(Decimal(2)/(8*k+4))-(Decimal(1)/(8*k+5))-(Decimal(1)/(8*k+6)))
k+=1
return pi
def main(argv):
if len(argv) !=2:
sys.exit('Usage: BaileyBorweinPlouffe.py <prec> <n>')
getcontext().prec=(int(sys.argv[1]))
my_pi=bbp(int(sys.argv[2]))
accuracy=100*(Decimal(math.pi)-my_pi)/my_pi
print"Pi is approximately "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if __name__=="__main__":
main(sys.argv[1:])Leaving aside the "wrapper" code, the function of BBP(N) is what you really want. The larger N you give it and the larger value you set to getcontext().prec, the more precise you will make the calculation. Let's look at some code results:
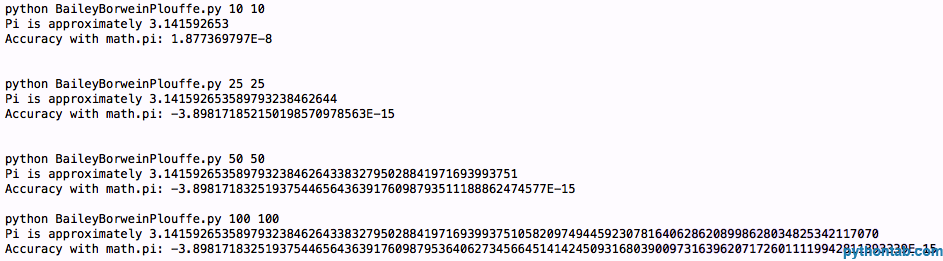
That's a lot of digital bits. You can see that we're no more accurate than before. So we need to move on to the next formula, Bellah's formula, and hopefully get better accuracy. It will look like this:
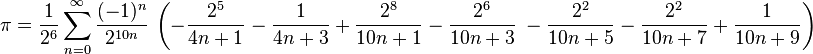
We will only change our transform formula, the rest of the code will remain the same. Click here to download Bella's formula implemented in Python. Let’s take a look at bellards(n):
def bellard(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(-1)**k/(1024**k))*( Decimal(256)/(10*k+1)+Decimal(1)/(10*k+9)-Decimal(64)/(10*k+3)-Decimal(32)/(4*k+1)-Decimal(4)/(10*k+5)-Decimal(4)/(10*k+7)-Decimal(1)/(4*k+3))
k+=1
pi=pi*1/(2**6)
return piOutput:
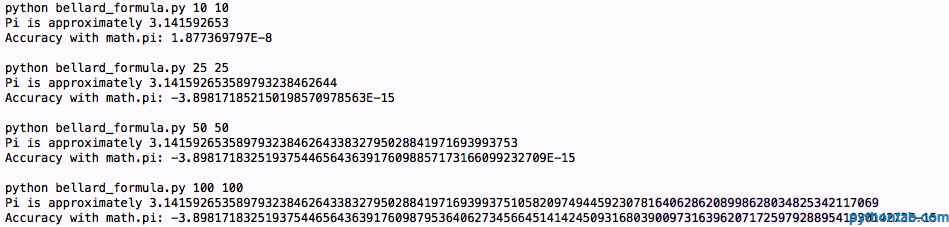
哦,不,我们得到的是同样的精度。好吧,让我们试试第三个公式, Chudnovsky 算法,它看起来是这个样子:
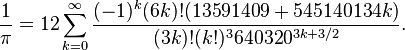
再一次,让我们看一下这个计算公式(假设我们有一个阶乘公式)。 点击这里可下载用 python 实现的 Chudnovsky 公式。
下面是程序和输出结果:
def chudnovsky(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(-1)**k)*(Decimal(factorial(6*k))/((factorial(k)**3)*(factorial(3*k)))*(13591409+545140134*k)/(640320**(3*k)))
k+=1
pi=pi*Decimal(10005).sqrt()/4270934400
pi=pi**(-1)
return pi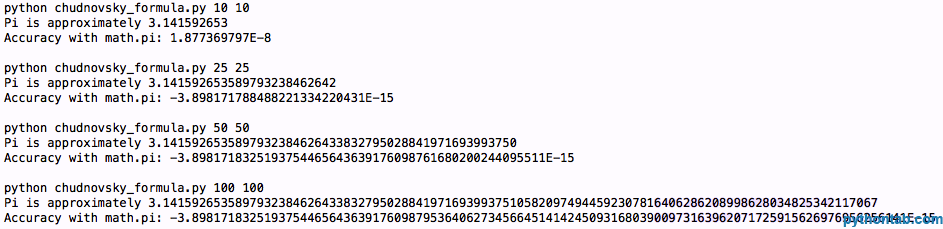
所以我们有了什么结论?花哨的算法不会使机器浮点世界达到更高标准。我真的很期待能有一个比我们用求和公式时所能得到的更好的精度。我猜那是过分的要求。如果你真的需要用PI,就只需使用math.pi变量了。然而,作为乐趣和测试你的计算机真的能有多快,你总是可以尝试第一个计算出Pi的百万位或者更多位是几。

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
 How to solve the permissions problem encountered when viewing Python version in Linux terminal?
Apr 01, 2025 pm 05:09 PM
How to solve the permissions problem encountered when viewing Python version in Linux terminal?
Apr 01, 2025 pm 05:09 PM
Solution to permission issues when viewing Python version in Linux terminal When you try to view Python version in Linux terminal, enter python...
 How to efficiently copy the entire column of one DataFrame into another DataFrame with different structures in Python?
Apr 01, 2025 pm 11:15 PM
How to efficiently copy the entire column of one DataFrame into another DataFrame with different structures in Python?
Apr 01, 2025 pm 11:15 PM
When using Python's pandas library, how to copy whole columns between two DataFrames with different structures is a common problem. Suppose we have two Dats...
 How to teach computer novice programming basics in project and problem-driven methods within 10 hours?
Apr 02, 2025 am 07:18 AM
How to teach computer novice programming basics in project and problem-driven methods within 10 hours?
Apr 02, 2025 am 07:18 AM
How to teach computer novice programming basics within 10 hours? If you only have 10 hours to teach computer novice some programming knowledge, what would you choose to teach...
 How to avoid being detected by the browser when using Fiddler Everywhere for man-in-the-middle reading?
Apr 02, 2025 am 07:15 AM
How to avoid being detected by the browser when using Fiddler Everywhere for man-in-the-middle reading?
Apr 02, 2025 am 07:15 AM
How to avoid being detected when using FiddlerEverywhere for man-in-the-middle readings When you use FiddlerEverywhere...
 How does Uvicorn continuously listen for HTTP requests without serving_forever()?
Apr 01, 2025 pm 10:51 PM
How does Uvicorn continuously listen for HTTP requests without serving_forever()?
Apr 01, 2025 pm 10:51 PM
How does Uvicorn continuously listen for HTTP requests? Uvicorn is a lightweight web server based on ASGI. One of its core functions is to listen for HTTP requests and proceed...
 What are some popular Python libraries and their uses?
Mar 21, 2025 pm 06:46 PM
What are some popular Python libraries and their uses?
Mar 21, 2025 pm 06:46 PM
The article discusses popular Python libraries like NumPy, Pandas, Matplotlib, Scikit-learn, TensorFlow, Django, Flask, and Requests, detailing their uses in scientific computing, data analysis, visualization, machine learning, web development, and H
 How to dynamically create an object through a string and call its methods in Python?
Apr 01, 2025 pm 11:18 PM
How to dynamically create an object through a string and call its methods in Python?
Apr 01, 2025 pm 11:18 PM
In Python, how to dynamically create an object through a string and call its methods? This is a common programming requirement, especially if it needs to be configured or run...
 How to solve permission issues when using python --version command in Linux terminal?
Apr 02, 2025 am 06:36 AM
How to solve permission issues when using python --version command in Linux terminal?
Apr 02, 2025 am 06:36 AM
Using python in Linux terminal...