 Java
Java
 javaTutorial
javaTutorial
 Summary of top 10 algorithm concepts commonly used in Java programming interviews
Summary of top 10 algorithm concepts commonly used in Java programming interviews
Summary of top 10 algorithm concepts commonly used in Java programming interviews
The following are the top 10 algorithm-related concepts in programming interviews. I will illustrate these concepts through some simple examples. Since fully mastering these concepts requires more effort, this list is intended only as an introduction. This article will look at the problem from a Java perspective, including the following concepts:
1. String
If the IDE does not have the code auto-completion function, you should remember the following methods.
toCharArray() // 获得字符串对应的char数组 Arrays.sort() // 数组排序Arrays.toString(char[] a) // 数组转成字符串 charAt(int x) // 获得某个索引处的字符 length() // 字符串长度 length // 数组大小
2. Linked list
In Java, the implementation of linked list is very simple. Each node Node has a value val and a link next pointing to the next node.
class Node {
int val;
Node next;
Node(int x) {
val = x;
next = null;
}
}Two famous applications of linked lists are Stack and Queue.
Stack:
class Stack{
Node top;
public Node peek(){
if(top != null){
return top;
}
return null;
}
public Node pop(){
if(top == null){
return null;
}else{
Node temp = new Node(top.val);
top = top.next;
return temp;
}
}
public void push(Node n){
if(n != null){
n.next = top;
top = n;
}
}
}Queue:
class Queue{
Node first, last;
public void enqueue(Node n){
if(first == null){
first = n;
last = first;
}else{
last.next = n;
last = n;
}
}
public Node dequeue(){
if(first == null){
return null;
}else{
Node temp = new Node(first.val);
first = first.next;
return temp;
}
}
}3. Tree
The tree here usually refers to a binary tree. Each node contains a left child node and a right child node, like the following:
class TreeNode{
int value;
TreeNode left;
TreeNode right;
}The following is the tree with Some related concepts:
Balanced vs. Unbalanced: In a balanced binary tree, the depth difference between the left and right subtrees of each node is at most 1 (1 or 0).
Full Binary Tree: Every node except the leaf nodes has two children.
Perfect Binary Tree: It is a full binary tree with the following properties: all leaf nodes have the same depth or are at the same level, and each parent node must have two children.
Complete Binary Tree: In a binary tree, every level except maybe the last one is completely filled, and all nodes must be as close to the left as possible.
Translator’s Note: A perfect binary tree is also vaguely called a complete binary tree. An example of a perfect binary tree is the ancestry graph of a person at a given depth, since every person must have two biological parents. A complete binary tree can be thought of as a perfect binary tree that can have a number of additional leaf nodes leaning to the left. Question: What is the difference between a perfect binary tree and a full binary tree? (Reference: http://xlinux.nist.gov/dads/HTML/perfectBinaryTree.html)
4. Graph
Graph-related issues are mainly focused on depth first search (depth first search) and breadth first search (breath first) search).
The following is a simple implementation of graph breadth first search.
1) Define GraphNode
class GraphNode{
int val;
GraphNode next;
GraphNode[] neighbors;
boolean visited;
GraphNode(int x) {
val = x;
}
GraphNode(int x, GraphNode[] n){
val = x;
neighbors = n;
}
public String toString(){
return "value: "+ this.val;
}
}2) Define a queue Queue
class Queue{
GraphNode first, last;
public void enqueue(GraphNode n){
if(first == null){
first = n;
last = first;
}else{
last.next = n;
last = n;
}
}
public GraphNode dequeue(){
if(first == null){
return null;
}else{
GraphNode temp = new GraphNode(first.val, first.neighbors);
first = first.next;
return temp;
}
}
}3) Use queue Queue to implement breadth-first search
public class GraphTest {
public static void main(String[] args) {
GraphNode n1 = new GraphNode(1);
GraphNode n2 = new GraphNode(2);
GraphNode n3 = new GraphNode(3);
GraphNode n4 = new GraphNode(4);
GraphNode n5 = new GraphNode(5);
n1.neighbors = new GraphNode[]{n2,n3,n5};
n2.neighbors = new GraphNode[]{n1,n4};
n3.neighbors = new GraphNode[]{n1,n4,n5};
n4.neighbors = new GraphNode[]{n2,n3,n5};
n5.neighbors = new GraphNode[]{n1,n3,n4};
breathFirstSearch(n1, 5);
}
public static void breathFirstSearch(GraphNode root, int x){
if(root.val == x)
System.out.println("find in root");
Queue queue = new Queue();
root.visited = true;
queue.enqueue(root);
while(queue.first != null){
GraphNode c = (GraphNode) queue.dequeue();
for(GraphNode n: c.neighbors){
if(!n.visited){
System.out.print(n + " ");
n.visited = true;
if(n.val == x)
System.out.println("Find "+n);
queue.enqueue(n);
}
}
}
}
}Output:
1 value: 2 value: 3 value: 5 Find value: 5
2 value: 4
5. Sorting
The following is the time complexity of different sorting algorithms. You can go to the wiki to take a look at the basic ideas of these algorithms.
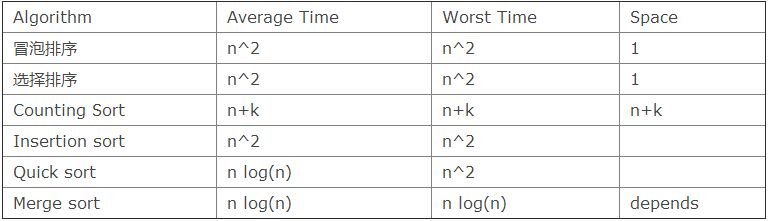
Also, here are some implementations/demos: Counting sort, Mergesort, Quicksort, InsertionSort.
"Visually intuitive experience of 7 commonly used sorting algorithms"
"Video: 6-minute demonstration of 15 sorting algorithms"
6. Recursion vs. Iteration
For programmers, recursion should be an innate A built-in thought can be illustrated with a simple example.
Question: There are n steps, and you can only go up 1 or 2 steps at a time. How many ways are there?
Step 1: Find the relationship between the first n steps and the first n-1 steps.
In order to walk up n steps, there are only two ways: climb 1 step from n-1 steps to get there or climb 2 steps from n-2 steps to get there. If f(n) is the number of ways to climb to the nth step, then f(n) = f(n-1) + f(n-2).
Step 2: Make sure the start conditions are correct.
f(0) = 0;
f(1) = 1;
public static int f(int n){
if(n <= 2) return n;
int x = f(n-1) + f(n-2);
return x;
}The time complexity of the recursive method is exponential in n, because there are many redundant calculations, as follows:
f(5) f(4) + f(3) f(3) + f(2) + f(2) + f(1) f(2) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1) f(1) + f(0) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)
The direct idea is to Convert recursion to iteration:
public static int f(int n) {
if (n <= 2){
return n;
}
int first = 1, second = 2;
int third = 0;
for (int i = 3; i <= n; i++) {
third = first + second;
first = second;
second = third;
}
return third;
}For this example, iteration takes less time, you may also want to take a look at Recursion vs Iteration.
7. Dynamic Programming
Dynamic programming is a technique for solving problems of the following nature:
A problem can be solved by solving smaller sub-problems (Translator’s Note: The optimal solution to the problem contains its sub-problems The optimal solution, that is, the optimal substructure properties).
The solutions to some sub-problems may need to be calculated multiple times (Translator’s Note: This is the overlapping nature of sub-problems).
The solutions to the subproblems are stored in a table, so that each subproblem only needs to be calculated once.
Requires extra space to save time.
The step climbing problem completely conforms to the above four properties, so it can be solved by dynamic programming method.
public static int[] A = new int[100];
public static int f3(int n) {
if (n <= 2)
A[n]= n;
if(A[n] > 0)
return A[n];
else
A[n] = f3(n-1) + f3(n-2);//store results so only calculate once!
return A[n];
}8. Bit operations
Bit operators:

获得给定数字n的第i位:(i从0计数并从右边开始)
public static boolean getBit(int num, int i){
int result = num & (1<<i);
if(result == 0){
return false;
}else{
return true;
}例如,获得数字10的第2位:
i=1, n=10
1<<1= 10
1010&10=10
10 is not 0, so return true;
9. 概率问题
解决概率相关的问题通常需要很好的规划了解问题(formatting the problem),这里刚好有一个这类问题的简单例子:
一个房间里有50个人,那么至少有两个人生日相同的概率是多少?(忽略闰年的事实,也就是一年365天)
计算某些事情的概率很多时候都可以转换成先计算其相对面。在这个例子里,我们可以计算所有人生日都互不相同的概率,也就是:365/365 * 364/365 * 363/365 * … * (365-49)/365,这样至少两个人生日相同的概率就是1 – 这个值。
public static double caculateProbability(int n){
double x = 1;
for(int i=0; i<n; i++){
x *= (365.0-i)/365.0;
}
double pro = Math.round((1-x) * 100);
return pro/100;calculateProbability(50) = 0.97
10. 排列组合
组合和排列的区别在于次序是否关键。
如果你有任何问题请在下面评论。
参考/推荐资料:
1. Binary tree
2. Introduction to Dynamic Programming
3. UTSA Dynamic Programming slides
4. Birthday paradox
5. Cracking the Coding Interview: 150 Programming Interview Questions and Solutions, Gayle Laakmann McDowell

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
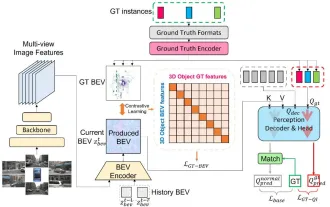 CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
Written above & the author’s personal understanding: At present, in the entire autonomous driving system, the perception module plays a vital role. The autonomous vehicle driving on the road can only obtain accurate perception results through the perception module. The downstream regulation and control module in the autonomous driving system makes timely and correct judgments and behavioral decisions. Currently, cars with autonomous driving functions are usually equipped with a variety of data information sensors including surround-view camera sensors, lidar sensors, and millimeter-wave radar sensors to collect information in different modalities to achieve accurate perception tasks. The BEV perception algorithm based on pure vision is favored by the industry because of its low hardware cost and easy deployment, and its output results can be easily applied to various downstream tasks.
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
The bottom layer of the C++sort function uses merge sort, its complexity is O(nlogn), and provides different sorting algorithm choices, including quick sort, heap sort and stable sort.
 Can artificial intelligence predict crime? Explore CrimeGPT's capabilities
Mar 22, 2024 pm 10:10 PM
Can artificial intelligence predict crime? Explore CrimeGPT's capabilities
Mar 22, 2024 pm 10:10 PM
The convergence of artificial intelligence (AI) and law enforcement opens up new possibilities for crime prevention and detection. The predictive capabilities of artificial intelligence are widely used in systems such as CrimeGPT (Crime Prediction Technology) to predict criminal activities. This article explores the potential of artificial intelligence in crime prediction, its current applications, the challenges it faces, and the possible ethical implications of the technology. Artificial Intelligence and Crime Prediction: The Basics CrimeGPT uses machine learning algorithms to analyze large data sets, identifying patterns that can predict where and when crimes are likely to occur. These data sets include historical crime statistics, demographic information, economic indicators, weather patterns, and more. By identifying trends that human analysts might miss, artificial intelligence can empower law enforcement agencies
 Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
01 Outlook Summary Currently, it is difficult to achieve an appropriate balance between detection efficiency and detection results. We have developed an enhanced YOLOv5 algorithm for target detection in high-resolution optical remote sensing images, using multi-layer feature pyramids, multi-detection head strategies and hybrid attention modules to improve the effect of the target detection network in optical remote sensing images. According to the SIMD data set, the mAP of the new algorithm is 2.2% better than YOLOv5 and 8.48% better than YOLOX, achieving a better balance between detection results and speed. 02 Background & Motivation With the rapid development of remote sensing technology, high-resolution optical remote sensing images have been used to describe many objects on the earth’s surface, including aircraft, cars, buildings, etc. Object detection in the interpretation of remote sensing images
 Practice and reflections on Jiuzhang Yunji DataCanvas multi-modal large model platform
Oct 20, 2023 am 08:45 AM
Practice and reflections on Jiuzhang Yunji DataCanvas multi-modal large model platform
Oct 20, 2023 am 08:45 AM
1. The historical development of multi-modal large models. The photo above is the first artificial intelligence workshop held at Dartmouth College in the United States in 1956. This conference is also considered to have kicked off the development of artificial intelligence. Participants Mainly the pioneers of symbolic logic (except for the neurobiologist Peter Milner in the middle of the front row). However, this symbolic logic theory could not be realized for a long time, and even ushered in the first AI winter in the 1980s and 1990s. It was not until the recent implementation of large language models that we discovered that neural networks really carry this logical thinking. The work of neurobiologist Peter Milner inspired the subsequent development of artificial neural networks, and it was for this reason that he was invited to participate in this project.
 Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
1. Background of the Construction of 58 Portraits Platform First of all, I would like to share with you the background of the construction of the 58 Portrait Platform. 1. The traditional thinking of the traditional profiling platform is no longer enough. Building a user profiling platform relies on data warehouse modeling capabilities to integrate data from multiple business lines to build accurate user portraits; it also requires data mining to understand user behavior, interests and needs, and provide algorithms. side capabilities; finally, it also needs to have data platform capabilities to efficiently store, query and share user profile data and provide profile services. The main difference between a self-built business profiling platform and a middle-office profiling platform is that the self-built profiling platform serves a single business line and can be customized on demand; the mid-office platform serves multiple business lines, has complex modeling, and provides more general capabilities. 2.58 User portraits of the background of Zhongtai portrait construction
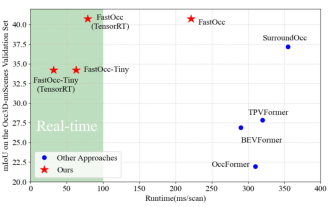 Add SOTA in real time and skyrocket! FastOcc: Faster inference and deployment-friendly Occ algorithm is here!
Mar 14, 2024 pm 11:50 PM
Add SOTA in real time and skyrocket! FastOcc: Faster inference and deployment-friendly Occ algorithm is here!
Mar 14, 2024 pm 11:50 PM
Written above & The author’s personal understanding is that in the autonomous driving system, the perception task is a crucial component of the entire autonomous driving system. The main goal of the perception task is to enable autonomous vehicles to understand and perceive surrounding environmental elements, such as vehicles driving on the road, pedestrians on the roadside, obstacles encountered during driving, traffic signs on the road, etc., thereby helping downstream modules Make correct and reasonable decisions and actions. A vehicle with self-driving capabilities is usually equipped with different types of information collection sensors, such as surround-view camera sensors, lidar sensors, millimeter-wave radar sensors, etc., to ensure that the self-driving vehicle can accurately perceive and understand surrounding environment elements. , enabling autonomous vehicles to make correct decisions during autonomous driving. Head



