Python data structure - implementation of stack and queue (1)

1. Stack

A stack is a table that restricts insertion and deletion operations to only one position. This position is the end of the table and is called the top of the stack. The basic operations of the stack are PUSH (into the stack) and POP (into the stack). The stack is also called a LIFO (last in, first out) table.

1.1 Stack implementation

class Stack(object):
    def __init__(self):
        self.stack=[]
    def isEmpty(self):
        return self.stack==[]
    def push(self,item):
        self.stack.append(item)
    def pop(self):
        if self.isEmpty():
            raise IndexError,'pop from empty stack'
        return self.stack.pop()
    def peek(self):
        return self.stack[-1]
    def size(self):
        return len(self.stack)

1.2 Stack application

1.2.1 Check the paired symbols in the program

Syntax errors in the program are often caused by missing a symbol. The stack can be used to check whether symbols are paired. Make an empty stack. If the character is an open symbol ('({[')), push it onto the stack. If the symbol is a closed symbol (')]}'), an error will be reported when the stack is empty, corresponding to '()}' mistake. Otherwise, pop the stack. If the popped symbol is not the corresponding open symbol, an error will be reported, corresponding to the error of '(}'. At the end of the file, if the stack is empty, an error will be reported, corresponding to the error of '({}'.

def match(i,j):
    opens='([{'
    closes=')]}'
    return opens.index(i)==closes.index(j)
def syntaxChecker(string):
    stack=Stack()
    balanced=True
    for i in string:
        if i in '([{':
            stack.push(i)
        elif i in ')]}':
            if stack.isEmpty():
                balanced=False
                break
            else:
                j=stack.pop()
                if not match(j,i):
                    balanced=False
                    break
    if not stack.isEmpty():
        balanced=False
    return balanced

1.2.2 Decimal conversion

Decimal conversion to binary: Convert decimal to binary until the quotient is 0. Start reading from the bottom left number, then read the numbers on the right, and read from bottom to top. Solving with Algorithms and Picture of "Data Structures":

Code:

def decimal_to_bin(dec):
    stack=Stack()
    cur=dec
    while cur>0:
        a=cur%2
        cur=cur/2
        stack.push(a)
    binstr=''
    while not stack.isEmpty():
        binstr+=str(stack.pop())
    return binstr

1.2.3 Postfix notation

Suffix notation (postfix), using a stack, pushing a number onto the stack when encountering an operation When the operator is used, it acts on the two elements popped from the stack and pops the result onto the stack.

(7+8)/(3+2) can be written as 7 8 + 3 2 + /

Picture from "Problem Solving with Algorithms and Data Structures":

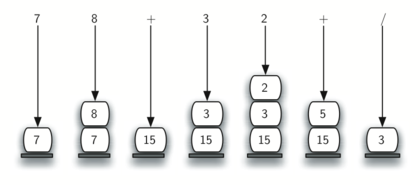Conversion from infix to suffix: When When an operand is read, it is put into the output. When the operator (+,-,*,/) is read, if the stack is empty, push it into the stack, otherwise pop the stack element and put it into the output until an element with a lower priority is found. After reading '(', push it onto the stack, and when reading ')', pop the stack elements and send them to the output until '(' is found. At the end, pop the stack elements until the stack becomes empty.

From " Picture of "Problem Solving with Algorithms and Data Structures":

def infixtoPostfix(infix):
    a={}
    a['*']=3
    a['/']=3
    a['+']=2
    a['-']=2
    a['(']=1
    stack=Stack()
    post=''
    for i in infix:
        if i not in a and i!=')':
            post+=i
        elif i=='(':
            stack.push(i)
        elif i==')':
            top=stack.pop()
            while top!='(':
                post+=top
                top=stack.pop()
        else:          
            while not stack.isEmpty() and a[i]<=a[stack.peek()]:
                post+=stack.pop()
            stack.push(i)
    while not stack.isEmpty():
        post+=stack.pop()
    return post
                   
def postfixExp(postfix):
    stack=Stack()
    postlist=postfix.split()
    for i in postlist:
        if i not in &#39;+-*/&#39;:
            stack.push(i)
        else:
            a=stack.pop()
            b=stack.pop()
            result=math(i,b,a)
            stack.push(result)
    return stack.pop()
def math(x,y,z):
    if x==&#39;+&#39;:
        return float(y)+float(z)
    if x==&#39;-&#39;:
        return float(y)-float(z)
    if x==&#39;*&#39;:
        return float(y)*float(z)
    if x==&#39;/&#39;:
        return float(y)/float(z)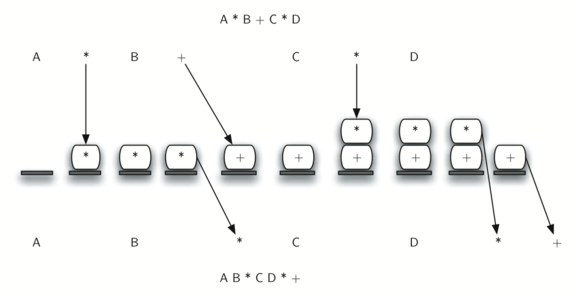

2 Queue

A queue is also a table. When using a queue, insertion and deletion are performed on different ends. The basic operation of the queue is Enqueue. , insert an element at the end of the table (rear), and dequeue (Dequeue), delete the element at the beginning of the table.

class Queue(object):
    def __init__(self):
        self.queue=[]
    def isEmpty(self):
        return self.queue==[]
    def enqueue(self,x):
        self.queue.append(x)
    def dequeue(self):
        if self.queue:
            a=self.queue[0]
            self.queue.remove(a)
            return a
        else:
            raise IndexError,'queue is empty'
    def size(self):
        return len(self.queue)

The above is the content of Python data structure - implementation of stack and queue (1), more related. Please follow the PHP Chinese website (www.php.cn) for articles