 Backend Development
Backend Development
 C#.Net Tutorial
C#.Net Tutorial
 Find the combination of any m numbers in a number of length n
Find the combination of any m numbers in a number of length n
Find the combination of any m numbers in a number of length n
The problem can be decomposed into:
1. First select the number with the largest number from n numbers, then select m-1 numbers from the remaining n-1 numbers, until n-(m-1) numbers are selected until 1 number is selected.
2. Select the next smallest number from n numbers and continue step 1 until the current number with the largest optional number is m.
Obviously, the above method is a recursive process, which means that all combinations can be obtained very cleanly using the recursive method.
Code:
package algorithm.ms100;
public class CtzHe {
private int[] array = {1,2,3,4,5};
private int[] b= new int[3];
private int M = 3;
public void combine( int a[], int n, int m)
{
for(int i=n; i>=m; i--) // 注意这里的循环范围
{
b[m-1] = i - 1;
if (m > 1)
combine(a,i-1,m-1);
else // m == 1, 输出一个组合
{
for(int j=M-1; j>=0; j--)
System.out.print( a[b[j]] + " ");
System.out.println();
}
}
}
public static void main(String[] args) {
CtzHe c = new CtzHe();
c.combine(c.array, 5, 3);
}
}
Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
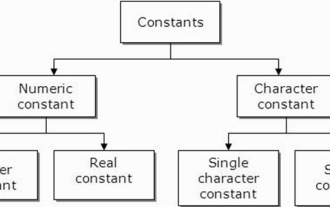 What are constants in C language? Can you give an example?
Aug 28, 2023 pm 10:45 PM
What are constants in C language? Can you give an example?
Aug 28, 2023 pm 10:45 PM
A constant is also called a variable and once defined, its value does not change during the execution of the program. Therefore, we can declare a variable as a constant referencing a fixed value. It is also called text. Constants must be defined using the Const keyword. Syntax The syntax of constants used in C programming language is as follows - consttypeVariableName; (or) consttype*VariableName; Different types of constants The different types of constants used in C programming language are as follows: Integer constants - For example: 1,0,34, 4567 Floating point constants - Example: 0.0, 156.89, 23.456 Octal and Hexadecimal constants - Example: Hex: 0x2a, 0xaa.. Octal
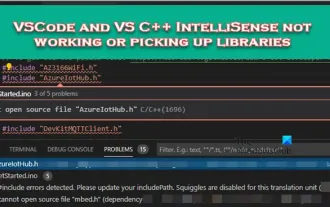 VSCode and VS C++ IntelliSense not working or picking up libraries
Feb 29, 2024 pm 01:28 PM
VSCode and VS C++ IntelliSense not working or picking up libraries
Feb 29, 2024 pm 01:28 PM
VS Code and Visual Studio C++ IntelliSense may not be able to pick up libraries, especially when working on large projects. When we hover over #Include<wx/wx.h>, we see the error message "CannotOpen source file 'string.h'" (depends on "wx/wx.h") and sometimes, autocomplete Function is unresponsive. In this article we will see what you can do if VSCode and VSC++ IntelliSense are not working or extracting libraries. Why doesn't my Intellisense work in C++? When working with large files, IntelliSense sometimes
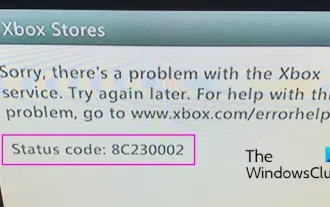 Fix Xbox error code 8C230002
Feb 27, 2024 pm 03:55 PM
Fix Xbox error code 8C230002
Feb 27, 2024 pm 03:55 PM
Are you unable to purchase or watch content on your Xbox due to error code 8C230002? Some users keep getting this error when trying to purchase or watch content on their console. Sorry, there's a problem with the Xbox service. Try again later. For help with this issue, visit www.xbox.com/errorhelp. Status Code: 8C230002 This error code is usually caused by temporary server or network problems. However, there may be other reasons, such as your account's privacy settings or parental controls, that may prevent you from purchasing or viewing specific content. Fix Xbox Error Code 8C230002 If you receive error code 8C when trying to watch or purchase content on your Xbox console
 Recursive program to find minimum and maximum elements of array in C++
Aug 31, 2023 pm 07:37 PM
Recursive program to find minimum and maximum elements of array in C++
Aug 31, 2023 pm 07:37 PM
We take the integer array Arr[] as input. The goal is to find the largest and smallest elements in an array using a recursive method. Since we are using recursion, we will iterate through the entire array until we reach length = 1 and then return A[0], which forms the base case. Otherwise, the current element is compared to the current minimum or maximum value and its value is updated recursively for subsequent elements. Let’s look at various input and output scenarios for this −Input −Arr={12,67,99,76,32}; Output −Maximum value in the array: 99 Explanation &mi
 China Eastern Airlines announces that C919 passenger aircraft will soon be put into actual operation
May 28, 2023 pm 11:43 PM
China Eastern Airlines announces that C919 passenger aircraft will soon be put into actual operation
May 28, 2023 pm 11:43 PM
According to news on May 25, China Eastern Airlines disclosed the latest progress on the C919 passenger aircraft at the performance briefing meeting. According to the company, the C919 purchase agreement signed with COMAC has officially come into effect in March 2021, and the first C919 aircraft has been delivered by the end of 2022. It is expected that the aircraft will be officially put into actual operation soon. China Eastern Airlines will use Shanghai as its main base for commercial operations of the C919, and plans to introduce a total of five C919 passenger aircraft in 2022 and 2023. The company stated that future introduction plans will be determined based on actual operating conditions and route network planning. According to the editor's understanding, the C919 is China's new generation of single-aisle mainline passenger aircraft with completely independent intellectual property rights in the world, and it complies with internationally accepted airworthiness standards. Should
 C++ program to print spiral pattern of numbers
Sep 05, 2023 pm 06:25 PM
C++ program to print spiral pattern of numbers
Sep 05, 2023 pm 06:25 PM
Displaying numbers in different formats is one of the basic coding problems of learning. Different coding concepts like conditional statements and loop statements. There are different programs in which we use special characters like asterisks to print triangles or squares. In this article, we will print numbers in spiral form, just like squares in C++. We take the number of rows n as input and start from the top left corner and move to the right, then down, then left, then up, then right again, and so on and so on. Spiral pattern with numbers 123456724252627282982340414243309223948494431102138474645321120373635343312191817161514
 The function of void keyword in C language
Feb 19, 2024 pm 11:33 PM
The function of void keyword in C language
Feb 19, 2024 pm 11:33 PM
void in C is a special keyword used to represent an empty type, which means data without a specific type. In C language, void is usually used in the following three aspects. The function return type is void. In C language, functions can have different return types, such as int, float, char, etc. However, if the function does not return any value, the return type can be set to void. This means that after the function is executed, it does not return a specific value. For example: voidhelloWorld()
 For the first time in 23 years, C# wins the TIOBE 2023 Programming Language of the Year Award
Jan 11, 2024 pm 04:45 PM
For the first time in 23 years, C# wins the TIOBE 2023 Programming Language of the Year Award
Jan 11, 2024 pm 04:45 PM
According to the TIOBE Programming Community Index, one of the benchmarks for measuring the popularity of programming languages, it is evaluated by collecting data from engineers, courses, vendors and search engines around the world. The TIOBE Index in January 2024 was released recently, and the official programming language rankings for 2023 were announced. C# won the TIOBE 2023 Programming Language of the Year. This is the first time that C# has won this honor in 23 years. TIOBE's official press release stated that C# has been in the top 10 for more than 20 years. Now it is catching up with the four major languages and has become the programming language with the largest growth in one year (+1.43%). It well-deserved to win this award. Ranked second are Scratch (+0.83%) and Fortran (+0



