Seven ways to realize the general term of Fibonacci sequence
1: Recursive implementation
Use the formula f[n]=f[n-1]+f[n-2] and calculate recursively in sequence. The recursive end condition is f[1]=1, f[2] =1.
2: Array implementation
The space complexity and time complexity are both 0(n), the efficiency is average, and it is faster than recursion.
Three: Vector
The time complexity is 0(n), and the time complexity is 0(1). I just don’t know whether vector is efficient or not. Of course, vector has its own attributes that will occupy resources. .
Four: Queue
Of course, queues are more suitable for implementing Fibonacci sequences than arrays. The time complexity and space complexity are the same as vector
f(n)=f(n-1)+f(n-2), f(n) is only related to f(n-1) and f(n-2), after f(n) enters the queue, f( n-2) can be dequeued.
5: Iterative implementation
Iterative implementation is the most efficient, with time complexity of 0(n) and space complexity of 0(1).
6: Formula Implementation
When I was searching Baidu, I found that the Fibonacci sequence has a formula, so it can be calculated using the formula.
Since the accuracy of the double type is not enough, the results calculated by the program will have errors. If the formula is expanded and calculated, the result will be correct.
The complete implementation code is as follows:
#include "iostream"
#include "queue"
#include "cmath"
using namespace std;
int fib1(int index) //递归实现
{
if(index<1)
{
return -1;
}
if(index==1 || index==2)
return 1;
return fib1(index-1)+fib1(index-2);
}
int fib2(int index) //数组实现
{
if(index<1)
{
return -1;
}
if(index<3)
{
return 1;
}
int *a=new int[index];
a[0]=a[1]=1;
for(int i=2;i<index;i++)
a[i]=a[i-1]+a[i-2];
int m=a[index-1];
delete a; //释放内存空间
return m;
}
int fib3(int index) //借用vector<int>实现
{
if(index<1)
{
return -1;
}
vector<int> a(2,1); //创建一个含有2个元素都为1的向量
a.reserve(3);
for(int i=2;i<index;i++)
{
a.insert(a.begin(),a.at(0)+a.at(1));
a.pop_back();
}
return a.at(0);
}
int fib4(int index) //队列实现
{
if(index<1)
{
return -1;
}
queue<int>q;
q.push(1);
q.push(1);
for(int i=2;i<index;i++)
{
q.push(q.front()+q.back());
q.pop();
}
return q.back();
}
int fib5(int n) //迭代实现
{
int i,a=1,b=1,c=1;
if(n<1)
{
return -1;
}
for(i=2;i<n;i++)
{
c=a+b; //辗转相加法(类似于求最大公约数的辗转相除法)
a=b;
b=c;
}
return c;
}
int fib6(int n)
{
double gh5=sqrt((double)5);
return (pow((1+gh5),n)-pow((1-gh5),n))/(pow((double)2,n)*gh5);
}
int main(void)
{
printf("%d\n",fib3(6));
system("pause");
return 0;
}Seven: Bipartite Matrix Method
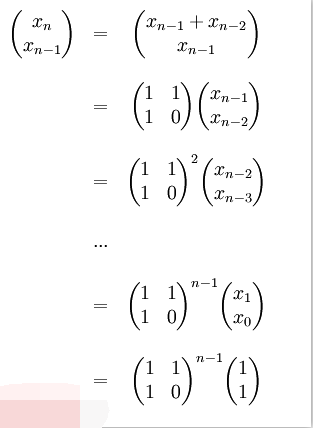
The code is posted below:
void multiply(int c[2][2],int a[2][2],int b[2][2],int mod)
{
int tmp[4];
tmp[0]=a[0][0]*b[0][0]+a[0][1]*b[1][0];
tmp[1]=a[0][0]*b[0][1]+a[0][1]*b[1][1];
tmp[2]=a[1][0]*b[0][0]+a[1][1]*b[1][0];
tmp[3]=a[1][0]*b[0][1]+a[1][1]*b[1][1];
c[0][0]=tmp[0]%mod;
c[0][1]=tmp[1]%mod;
c[1][0]=tmp[2]%mod;
c[1][1]=tmp[3]%mod;
}//计算矩阵乘法,c=a*b
int fibonacci(int n,int mod)//mod表示数字太大时需要模的数
{
if(n==0)return 0;
else if(n<=2)return 1;//这里表示第0项为0,第1,2项为1
int a[2][2]={{1,1},{1,0}};
int result[2][2]={{1,0},{0,1}};//初始化为单位矩阵
int s;
n-=2;
while(n>0)
{
if(n%2 == 1)
multiply(result,result,a,mod);
multiply(a,a,a,mod);
n /= 2;
}//二分法求矩阵幂
s=(result[0][0]+result[0][1])%mod;//结果
return s;
}int pow(int a,int n)
{
int ans=1;
while(n)
{
if(n&1)
ans*=a;
a*=a;
n>>=1;
}
return ans;
}
Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 11 Best PHP URL Shortener Scripts (Free and Premium)
Mar 03, 2025 am 10:49 AM
11 Best PHP URL Shortener Scripts (Free and Premium)
Mar 03, 2025 am 10:49 AM
Long URLs, often cluttered with keywords and tracking parameters, can deter visitors. A URL shortening script offers a solution, creating concise links ideal for social media and other platforms. These scripts are valuable for individual websites a
 Working with Flash Session Data in Laravel
Mar 12, 2025 pm 05:08 PM
Working with Flash Session Data in Laravel
Mar 12, 2025 pm 05:08 PM
Laravel simplifies handling temporary session data using its intuitive flash methods. This is perfect for displaying brief messages, alerts, or notifications within your application. Data persists only for the subsequent request by default: $request-
 Build a React App With a Laravel Back End: Part 2, React
Mar 04, 2025 am 09:33 AM
Build a React App With a Laravel Back End: Part 2, React
Mar 04, 2025 am 09:33 AM
This is the second and final part of the series on building a React application with a Laravel back-end. In the first part of the series, we created a RESTful API using Laravel for a basic product-listing application. In this tutorial, we will be dev
 Simplified HTTP Response Mocking in Laravel Tests
Mar 12, 2025 pm 05:09 PM
Simplified HTTP Response Mocking in Laravel Tests
Mar 12, 2025 pm 05:09 PM
Laravel provides concise HTTP response simulation syntax, simplifying HTTP interaction testing. This approach significantly reduces code redundancy while making your test simulation more intuitive. The basic implementation provides a variety of response type shortcuts: use Illuminate\Support\Facades\Http; Http::fake([ 'google.com' => 'Hello World', 'github.com' => ['foo' => 'bar'], 'forge.laravel.com' =>
 cURL in PHP: How to Use the PHP cURL Extension in REST APIs
Mar 14, 2025 am 11:42 AM
cURL in PHP: How to Use the PHP cURL Extension in REST APIs
Mar 14, 2025 am 11:42 AM
The PHP Client URL (cURL) extension is a powerful tool for developers, enabling seamless interaction with remote servers and REST APIs. By leveraging libcurl, a well-respected multi-protocol file transfer library, PHP cURL facilitates efficient execution of various network protocols, including HTTP, HTTPS, and FTP. This extension offers granular control over HTTP requests, supports multiple concurrent operations, and provides built-in security features.
 12 Best PHP Chat Scripts on CodeCanyon
Mar 13, 2025 pm 12:08 PM
12 Best PHP Chat Scripts on CodeCanyon
Mar 13, 2025 pm 12:08 PM
Do you want to provide real-time, instant solutions to your customers' most pressing problems? Live chat lets you have real-time conversations with customers and resolve their problems instantly. It allows you to provide faster service to your custom
 Announcement of 2025 PHP Situation Survey
Mar 03, 2025 pm 04:20 PM
Announcement of 2025 PHP Situation Survey
Mar 03, 2025 pm 04:20 PM
The 2025 PHP Landscape Survey investigates current PHP development trends. It explores framework usage, deployment methods, and challenges, aiming to provide insights for developers and businesses. The survey anticipates growth in modern PHP versio
 Notifications in Laravel
Mar 04, 2025 am 09:22 AM
Notifications in Laravel
Mar 04, 2025 am 09:22 AM
In this article, we're going to explore the notification system in the Laravel web framework. The notification system in Laravel allows you to send notifications to users over different channels. Today, we'll discuss how you can send notifications ov






