
Spiral motion implementation based on spiral queue logic
The reverse method of the spiral queue algorithm controls the two-axis motor to move according to the spiral trajectory, as shown below.
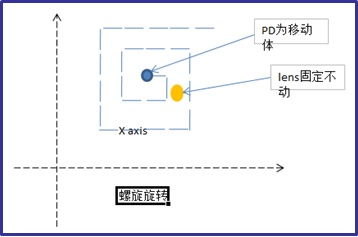
#1. Spiral Queue Algorithm Analysis
The following figure is a spiral queue. Assume that the coordinates of 1 are (0, 0), the x direction is positive to the right, and the y direction is positive downward. For example, the coordinates of 7 are (-1, -1), and the coordinates of 2 are (1, 0). Programming allows you to input the coordinates (x, y) of any point and output the corresponding number! (Reprinted from the Internet)
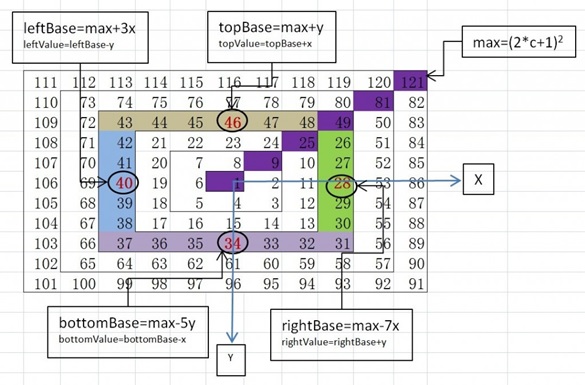
Maximum value per circle max=(2*c+1)(2*c+1), c It is the number of turns from inside to outside.
The differences between these reference values and max are 1C (top), 3C (left), 5C (bottom), 7C (right) (C represents the current number of laps), on the top and bottom, y The coordinate represents (or is equal to) the number of circles (i.e. C=y), while on the left and right the x-coordinate represents (or is equal to) the number of circles (i.e. C=x). Therefore, the difference mentioned earlier can be expressed as 1y, 3x, 5y, 7x using coordinates.
Code implementation:
private static Object spiral(int x, int y)
{
int c = max(abs(x), abs(y));// 当前坐标所在圈
int max = (c * 2 + 1) * (c * 2 + 1);// 当前圈上最大值
if (y == -c) { // 上边
return max + (x + y);
} else if (x == -c) {// 左边
return max + (3 * x - y);
} else if (y == c) {// 下边
return max + (-x - 5 * y);
} else {// 右边
return max + (-7 * x + y);
}
}2. Spiral motion
First customize the coordinate operation to represent the logical position of the PD.
struct Coordinate
{ public int X; public int Y; public Coordinate(int a, int b)
{
X = a;
Y = b;
} public static bool operator ==(Coordinate loc1, Coordinate loc2)
{ return (loc1.X == loc2.X) && (loc1.Y == loc2.Y);
} public static bool operator !=(Coordinate loc1, Coordinate loc2)
{ return !(loc1 == loc2);
} public override bool Equals(object loc)
{ return this == (Coordinate)loc;
} public override int GetHashCode()
{ return base.GetHashCode();
} public static Coordinate operator -(Coordinate loc1, Coordinate loc2)
{ return new Coordinate(loc1.X - loc2.X, loc1.Y - loc2.Y);
} public static Coordinate operator +(Coordinate loc1, Coordinate loc2)
{ return new Coordinate(loc1.X + loc2.X, loc1.Y + loc2.Y);
} public override string ToString()
{ return "(" + X + "," + Y + ")";
}
}Then reverse the method and calculate the x and y coordinates based on the number of steps.
public Coordinate ToLocation(int step, int pulse)
{
int c = (int)Math.Ceiling((Math.Sqrt(step) - 1) / 2);
int max = (int)Math.Pow(2 * c + 1, 2);
int x, y;
y = -c;//top
x = -(max + y - step);
if (Math.Abs(x) <= Math.Abs(y))
{
this.location.X = x * pulse;
this.location.Y = y * pulse;
return this.location;
}
x = -c;//left
y = max + 3 * x - step;
if (Math.Abs(y) <= Math.Abs(x))
{
this.location.X = x * pulse;
this.location.Y = y * pulse;
return this.location;
}
y = c;//bottom
x = max - 5 * y - step;
if (Math.Abs(x) <= Math.Abs(y))
{
this.location.X = x * pulse;
this.location.Y = y * pulse;
return this.location;
}
x = c;//right
y = -(max - 7 * x - step);
this.location.X = x * pulse;
this.location.Y = y * pulse;
//LocChange();
return this.location;
}Finally, the movement is realized according to the change of coordinates.
public void Start()
{
Coordinate moveToLoc, currentLoc, deltaLoc;
currentLoc = ToLocation(1, 0);
logInfo = string.Format("{0}: {1}{2}.", DateTime.Now.ToString("HH:mm:ss"), "the start location is ", currentLoc.ToString());
log.SaveLogToTxt(logInfo);
logInfo = string.Format("{0}: {1}.", DateTime.Now.ToString("HH:mm:ss"), "begin to move... ");
log.SaveLogToTxt(logInfo);
for (int step = 1; step <= this.roMaxStep[0]; step++)
{
moveToLoc = ToLocation(step + 1, this.roPulse[0]);
deltaLoc = moveToLoc - currentLoc;
logInfo = string.Format("{0}: step{1}{2}{3}...", DateTime.Now.ToString("HH:mm:ss"), step + " ", "move to ", moveToLoc.ToString());
log.SaveLogToTxt(logInfo);
bool moveX = card.MoveX(deltaLoc.X);
bool moveY = card.MoveY(deltaLoc.Y);
if (moveX == false || moveY == false)
//throw error
return;
currentLoc = moveToLoc;
//if RES > RoRESTarget
//break;
}
logInfo = string.Format("{0}: {1}.", DateTime.Now.ToString("HH:mm:ss"), "move done");
log.SaveLogToTxt(logInfo);
logInfo = string.Format("{0}: {1}{2}.", DateTime.Now.ToString("HH:mm:ss"), "the current location is ", currentLoc.ToString());
log.SaveLogToTxt(logInfo);
}The above is the content of Self-Study C#07 from 0-Spiral Queue and Spiral Movement. For more related content, please pay attention to the PHP Chinese website (www.php.cn)!




