python development compiler

引言

最近刚刚用python写完了一个解析protobuf文件的简单编译器，深感ply实现词法分析和语法分析的简洁方便。乘着余热未过，头脑清醒，记下一点总结和心得，方便各位pythoner参考使用。

ply使用

简介

如果你不是从事编译器或者解析器的开发工作，你可能从未听说过ply。ply是基于python的lex和yacc，而它的作者就是大名鼎鼎Python Cookbook, 3rd Edition的作者。可能有些朋友就纳闷了，我一个业务开发怎么需要自己写编译器呢，各位编程大牛说过，中央决定了，要多尝试新的东西。而且了解一些语法解析的姿势，以后自己解析格式复杂的日志或者数学公式，也是非常有帮助的。

针对没有编译基础的童鞋，强烈建议了解一些文法相关的基本概念。轮子哥强烈推荐的parsing techniques以及编译龙虎鲸书，个人感觉都不适合入门学习，在此推荐胡伦俊的编译原理（电子工业出版社），针对概念的例子讲解很多，很适合入门学习。当然也不需要特别深入研究，知道词法分析和语法分析的相关概念和方法就可以愉快的使用ply了。文档链接： http://www.pchou.info/open-source/2014/01/18/52da47204d4cb.html

为了方便大家上手，以求解多元一次方程组为例，讲解一下ply的使用。

例子说明

输入是多个格式为x + 4y - 3.2z = 7的一次方程，为了让例子尽可能简单，做如下限制：

• 每个方程含有变量的部分在等号左边，常数在等号右边

• 每个方程不限制变量的个数以及变量的顺序，但每个方程每个变量只允许出现一次

• 变量的命令规则为小写字母串（x y xx yy abc 均为合法变量名）

• 变量的系数限制为整数和浮点数，浮点数不允许1.4e8的格式，系数和变量紧邻，且系数不能为0

• 方程组和方程组之间用, ;隔开

学过线性代数的童鞋肯定知道，只需要将方程组抽象为矩阵，按照线性代数的方法就可以解决。因此只需要将输入方程组解析成右边的矩阵和变量列表即可，剩下的求解过程就可以交给线性代数相关的工具解决。

 

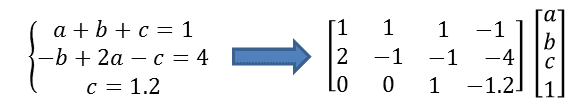
解析

词法解析

ply中的lex来做词法解析，词法解析的理论有一大堆，但是lex用起来却非常直观，就是用正则表达式的方式将文本字符串解析为一个一个的token，下面的代码就是用lex实现词法解析。

from ply import lex
 
# 
空格 制表符 回车这些不可见符号都忽略
t_ignore = ' \t\r'
 
# 
解析错误的时候直接抛出异常
def t_error(t):
    raise Exception('error {} at line {}'.format(t.value[0], t.lineno))
 
# 
记录行号，方便出错定位
def t_newline(t):
    r'\n+'
    t.lexer.lineno += len(t.value)
 
# 
支持c++风格的\\注释
def t_ignore_COMMENT(t):
    r'\/\/[^\n]*'
 
# 
变量的命令规则
def t_VARIABLE(t):
    r'[a-z]+'
    return t
 
# 
常数命令规则
def t_CONSTANT(t):
    r'\d+(\.\d+)?'
    t.value = float(t.value)
    return t
 
# 
输入中支持的符号头token，当然也支持t_PLUS = r'\+'的方式将加号定义为token
literals = '+-,;='
tokens = ('VARIABLE', 'CONSTANT')
 
 
if __name__ == '__main__':
    data = '''
    -x 
+ 2.4y + z = 0; //this is a comment
    9y 
- z + 7.2x = -1;
    y 
- z + x = 8
    '''
 
    lexer = lex.lex()
    lexer.input(data)
    while True:
        tok = lexer.token()
        if not tok:
            break
        print tok

直接运行文件就可以将解析的token串打印出来，如下所示，详细的使用文档可以参考ply文档。

LexToken(-,'-',2,5)
LexToken(VARIABLE,'x',2,6)
LexToken(+,'+',2,8)
LexToken(CONSTANT,2.4,2,10)
LexToken(VARIABLE,'y',2,13)
LexToken(+,'+',2,15)
LexToken(VARIABLE,'z',2,17)
LexToken(=,'=',2,19)
LexToken(CONSTANT,0.0,2,21)
LexToken(;,';',2,22)

语法解析

ply中的yacc用作语法分析，虽然复杂的词法分析可以代替简单的语法分析，但类似于编程语言的解析再复杂的词法分析也胜任不了。在使用yacc之前，需要了解上下文无关文法，这部分内容太多太杂，我也只了解部分简单的概念，有兴趣的可以看一看编译原理深入了解。

目前语法分析的方法有两大类，即自下向上的分析方法和自上而下的分析方法。所谓自上而下的分下法就是从文法的开始符号出发，根据文法规则正向推到出给定句子的一种方法，或者说，从树根开始，往下构造语法树，直到建立每个树叶的分析方法。代表算法是LL(1)，此算法文法解析能力不强，对文法定义要求比较高，主流的编译器都没有使用。自下而上的分析法是从给定的输入串开始，根据文法规则逐步进行归约，直至归约到文法的开始符号，或者说从语法书的末端开始，步步向上归约，直至归约到根节点的分析方法。代表算法有SLR、LRLR，ply使用的就是LRLR。

因此我们只需要定义文法和规约动作即可，以下就是完整的代码。

# 
-*- coding=utf8 -*-
 
from ply import (
    lex,
    yacc
)
 
# 
空格 制表符 回车这些不可见符号都忽略
t_ignore = ' \t\r'
 
# 
解析错误的时候直接抛出异常
def t_error(t):
    raise Exception('error {} at line {}'.format(t.value[0], t.lineno))
 
# 
记录行号，方便出错定位
def t_newline(t):
    r'\n+'
    t.lexer.lineno += len(t.value)
 
# 
支持c++风格的\\注释
def t_ignore_COMMENT(t):
    r'\/\/[^\n]*'
 
# 
变量的命令规则
def t_VARIABLE(t):
    r'[a-z]+'
    return t
 
# 
常数命令规则
def t_CONSTANT(t):
    r'\d+(\.\d+)?'
    t.value = float(t.value)
    return t
 
# 
输入中支持的符号头token，当然也支持t_PLUS = r'\+'的方式将加号定义为token
literals = '+-,;='
tokens = ('VARIABLE', 'CONSTANT')
 
# 
顶层文法，规约的时候equations对应的p[1]是一个列表，包含了方程左边各个变量与系数还有方程左边的常数
def p_start(p):
    """start : equations"""
    var_count, var_list = 0, []
    for left, _ in p[1]:
        for con, var_name in left:
            if var_name in var_list:
                continue
            var_list.append(var_name)
            var_count += 1
 
    matrix = [[0] * (var_count + 1) for _ in xrange(len(p[1]))]
    for counter, eq in enumerate(p[1]):
        left, right = eq
        for con, var_name in left:
            matrix[counter][var_list.index(var_name)] = con
        matrix[counter][-1] = -right
 
    var_list.append(1)
    p[0] = matrix, var_list
 
# 
方程组对应的文法，每个方程用，或者；做分隔
def p_equations(p):
    """equations : equation ',' equations
                 | equation ';' equations
                 | equation"""
    if len(p) == 2:
        p[0] = [p[1]]
    else:
        p[0] = [p[1]] + p[3]
 
# 
单个方程对应的文法
def p_equation(p):
    """equation : eq_left '=' eq_right"""
    p[0] = (p[1], p[3])
 
# 
方程等式左边对应的文法
def p_eq_left(p):
    """eq_left : var_unit eq_left
               |"""
    if len(p) == 1:
        p[0] = []
    else:
        p[0] = [p[1]] + p[2]
 
# 
六种文法对应例子： x, 5x, +x, -x, +4x, -4y
# 
归约的形式是一个元组，例： (5, 'x')
def p_var_unit(p):
    """var_unit : VARIABLE
                | 
CONSTANT VARIABLE
                | 
'+' VARIABLE
                | 
'-' VARIABLE
                | 
'+' CONSTANT VARIABLE
                | 
'-' CONSTANT VARIABLE"""
    len_p = len(p)
    if len_p == 2:
        p[0] = (1.0, p[1])
    elif len_p == 3:
        if p[1] == '+':
            p[0] = (1.0, p[2])
        elif p[1] == '-':
            p[0] = (-1.0, p[2])
        else:
            p[0] = (p[1], p[2])
    else:
        if p[1] == '+':
            p[0] = (p[2], p[3])
        else:
            p[0] = (-p[2], p[3])
 
# 
方程等式右边对应的常数，对应的例子：1.2， +1.2， -1.2
def p_eq_right(p):
    """eq_right : CONSTANT
                | 
'+' CONSTANT
                | 
'-' CONSTANT"""
    if len(p) == 3:
        if p[1] == '-':
            p[0] = -p[2]
        else:
            p[0] = p[2]
    else:
        p[0] = p[1]
 
if __name__ == '__main__':
    data = '''
    -x 
+ 2.4y + z = 0; //this is a comment
    9y 
- z + 7.2x = -1;
    y 
- z + x = 8
    '''
 
    lexer = lex.lex()
    parser = yacc.yacc(debug=True)
    lexer.lineno = 1
    s = parser.parse(data)
    print s

直接运行文件即可，得到的输出如下，之后就可以根据线性代数的方法求解各个变量的值

([[-1.0, 2.4, 1.0, 
-0.0], [7.2, 9.0, -1.0, 1.0], [1.0, 1.0, -1.0, -8.0]], ['x', 'y', 'z', 
1])

总结

依托于python简洁的语法，ply为我们提供了一个强大的语法分析工具，更复杂的例子可以参考https://github.com/LiuRoy/proto_parser，这是我用ply实现的一个简单的protobuf解析器，用于减少频繁的中间文件生成。有这种神器，一颗赛艇！

The above is the content of python development compiler. For more related content, please pay attention to the PHP Chinese website (www.php.cn)!