
Stack(stack)
The stack is also called a stack. It is a special ordered list. The insertion and deletion operations are performed on the top of the stack and follow the rules of first-in, last-out and last-in-first-out. carry out operations.
As shown in the picture below
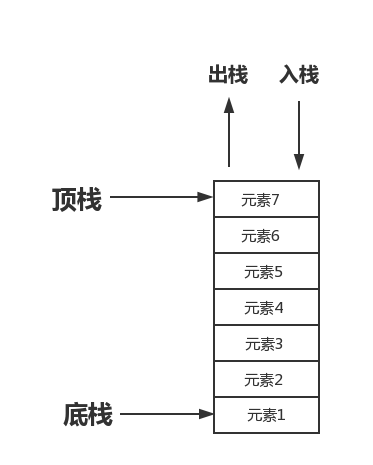
For example, in the magazine of a gun, the first bullet put into the magazine is the last one when fired. The last bullet put into the magazine is the first bullet fired when fired.
Stack interface
If you create a stack, then you should have the following interface to operate the stack
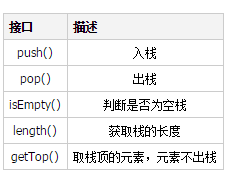
Know After the stack requires the above interface, then in Python, the list is similar to a stack, and the interface provided is as follows:
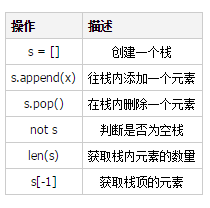
Usage example of the stack interface in Python:
# 创建一个栈 In [1]: s = [] # 往栈内添加一个元素 In [2]: s.append(1) In [3]: s Out[3]: [1] # 删除栈内的一个元素 In [4]: s.pop() Out[4]: 1 In [5]: s Out[5]: [] # 判断栈是否为空 In [6]: not s Out[6]: True In [7]: s.append(1) In [8]: not s Out[8]: False # 获取栈内元素的数量 In [9]: len(s) Out[9]: 1 In [10]: s.append(2) In [11]: s.append(3) # 取栈顶的元素 In [12]: s[-1] Out[12]: 3
A large number of examples
After understanding the basic concepts of the stack, let us look at a few more examples to facilitate our understanding of the stack.
Bracket matching
Question
If the expression is allowed to contain three square brackets (), [], {}, the nesting order is arbitrary, for example:
Correct format
{()[()]},[{({})}]Incorrect format
[(]),[()),(()}
Write a function to determine whether an expression string and bracket matching are correct
Ideas
Create an empty stack to store left brackets that have not yet been found;
Convenience strings, push the stack when encountering a left bracket, and pop a left bracket for matching when encountering a right bracket;
During the second step, if the right bracket is encountered when the stack is empty, it means that the left bracket is missing and does not match;
At the end of the second step traversal, the stack is not empty, indicating that it is missing Right bracket, mismatch;
Solution code
It is recommended to break points in pycharm for better understanding
#!/use/bin/env python
# _*_ coding:utf-8 _*_
LEFT = {'(', '[', '{'} # 左括号
RIGHT = {')', ']', '}'} # 右括号
def match(expr):
"""
:param expr: 传过来的字符串
:return: 返回是否是正确的
"""
stack = [] # 创建一个栈
for brackets in expr: # 迭代传过来的所有字符串
if brackets in LEFT: # 如果当前字符在左括号内
stack.append(brackets) # 把当前左括号入栈
elif brackets in RIGHT: # 如果是右括号
if not stack or not 1 <= ord(brackets) - ord(stack[-1]) <= 2:
# 如果当前栈为空,()]
# 如果右括号减去左括号的值不是小于等于2大于等于1
return False # 返回False
stack.pop() # 删除左括号
return not stack # 如果栈内没有值则返回True,否则返回False
result = match('[(){()}]')
print(result)
Maze problem
Question
Use a two-dimensional array to represent a simple maze, use 0 to represent the passage, and use 1 to represent the block. The mouse can Move the adjacent four points of southeast, northwest, and design an algorithm to simulate a mouse walking through a maze and find a path from the entrance to the exit.
As shown in the picture
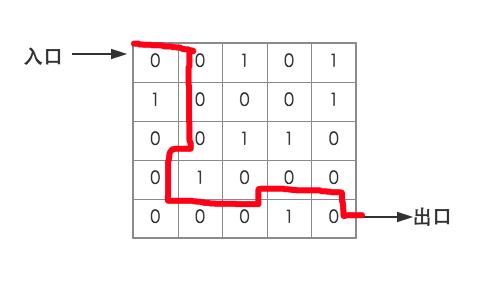
The correct route to go out is shown as the red line in the picture
Thinking
Use A stack to record the path of the mouse from the entrance to the exit
After reaching a certain point, push the left side of the point onto the stack and set the value of the point to 1, indicating that it has passed;
Select any one of the reachable points from the four adjacent points and walk to that point;
If you do not go to the four adjacent points after reaching a certain point, it means you have reached a dead end. At this time Back off the stack, go back one step and try other points;
Repeat steps two, three, and four until you find the exit;
Solution code
#!/use/bin/env python # _*_ coding:utf-8 _*_ def initMaze(): """ :return: 初始化迷宫 """ maze = [[0] * 7 for _ in range(5 + 2)] # 用列表解析创建一个7*7的二维数组,为了确保迷宫四周都是墙 walls = [ # 记录了墙的位置 (1, 3), (2, 1), (2, 5), (3, 3), (3, 4), (4, 2), # (4, 3), # 如果把(4, 3)点也设置为墙,那么整个迷宫是走不出去的,所以会返回一个空列表 (5, 4) ] for i in range(7): # 把迷宫的四周设置成墙 maze[i][0] = maze[i][-1] = 1 maze[0][i] = maze[-1][i] = 1 for i, j in walls: # 把所有墙的点设置为1 maze[i][j] = 1 return maze """ [1, 1, 1, 1, 1, 1, 1] [1, 0, 0, 1, 0, 0, 1] [1, 1, 0, 0, 0, 1, 1] [1, 0, 0, 1, 1, 0, 1] [1, 0, 1, 0, 0, 0, 1] [1, 0, 0, 0, 1, 0, 1] [1, 1, 1, 1, 1, 1, 1] """ def path(maze, start, end): """ :param maze: 迷宫 :param start: 起始点 :param end: 结束点 :return: 行走的每个点 """ i, j = start # 分解起始点的坐标 ei, ej = end # 分解结束点的左边 stack = [(i, j)] # 创建一个栈,并让老鼠站到起始点的位置 maze[i][j] = 1 # 走过的路置为1 while stack: # 栈不为空的时候继续走,否则退出 i, j = stack[-1] # 获取当前老鼠所站的位置点 if (i, j) == (ei, ej): break # 如果老鼠找到了出口 for di, dj in [(0, -1), (0, 1), (-1, 0), (1, 0)]: # 左右上下 if maze[i + di][j + dj] == 0: # 如果当前点可走 maze[i + di][j + dj] = 1 # 把当前点置为1 stack.append((i + di, j + dj)) # 把当前的位置添加到栈里面 break else: # 如果所有的点都不可走 stack.pop() # 退回上一步 return stack # 如果迷宫不能走则返回空栈 Maze = initMaze() # 初始化迷宫 result = path(maze=Maze, start=(1, 1), end=(5, 5)) # 老鼠开始走迷宫 print(result) # [(1, 1), (1, 2), (2, 2), (3, 2), (3, 1), (4, 1), (5, 1), (5, 2), (5, 3), (4, 3), (4, 4), (4, 5), (5, 5)]
Evaluation of postfix expressions
Question
When evaluating an expression, the compiler usually uses a postfix expression, which does not require parentheses:
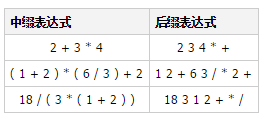
Write a program to implement the postfix expression evaluation function.
Idea
Create a stack to store the operands to be calculated;
Traverse the string, push the operand into the stack when encountering it, and pop it out when encountering the operation symbol Stack operands (n times), perform corresponding calculations, the calculation result is the new operand pushed back onto the stack, waiting for calculation
Follow the above process, traverse the entire expression, and only the final result remains on the stack ;
Solution code
#!/use/bin/env python
# _*_ coding:utf-8 _*_
operators = { # 运算符操作表
'+': lambda op1, op2: op1 + op2,
'-': lambda op1, op2: op1 - op2,
'*': lambda op1, op2: op1 * op2,
'/': lambda op1, op2: op1 / op2,
}
def evalPostfix(e):
"""
:param e: 后缀表达式
:return: 正常情况下栈内的第一个元素就是计算好之后的值
"""
tokens = e.split() # 把传过来的后缀表达式切分成列表
stack = []
for token in tokens: # 迭代列表中的元素
if token.isdigit(): # 如果当前元素是数字
stack.append(int(token)) # 就追加到栈里边
elif token in operators.keys(): # 如果当前元素是操作符
f = operators[token] # 获取运算符操作表中对应的lambda表达式
op2 = stack.pop() # 根据先进后出的原则,先让第二个元素出栈
op1 = stack.pop() # 在让第一个元素出栈
stack.append(f(op1, op2)) # 把计算的结果在放入到栈内
return stack.pop() # 返回栈内的第一个元素
result = evalPostfix('2 3 4 * +')
print(result)
# 14Backpack problem
Question
There is a backpack that can hold 10kg of items. Now there are 6 items: :
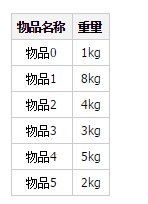
Written to find all the solutions that can fill the backpack, such as Item 1 + Item 5.
Solution to the code
#!/use/bin/env python # _*_ coding:utf-8 _*_ def knapsack(t, w): """ :param t: 背包总容量 :param w: 物品重量列表 :return: """ n = len(w) # 可选的物品数量 stack = [] # 创建一个栈 k = 0 # 当前所选择的物品游标 while stack or k < n: # 栈不为空或者k<n while t > 0 and k < n: # 还有剩余空间并且有物品可装 if t >= w[k]: # 剩余空间大于等于当前物品重量 stack.append(k) # 把物品装备背包 t -= w[k] # 背包空间减少 k += 1 # 继续向后找 if t == 0: # 找到了解 print(stack) # 回退过程 k = stack.pop() # 把最后一个物品拿出来 t += w[k] # 背包总容量加上w[k] k += 1 # 装入下一个物品 knapsack(10, [1, 8, 4, 3, 5, 2]) """ [0, 2, 3, 5] [0, 2, 4] [1, 5] [3, 4, 5] """
Summary
The above is the entire content of this article. I hope that the content of this article can bring some help to everyone's study or work. If If you have any questions, you can leave a message to communicate.
For more detailed explanations of the practical stack of Python algorithm applications, please pay attention to the PHP Chinese website!




