 Backend Development
Backend Development
 PHP Tutorial
PHP Tutorial
 Looking at 'recursion' from the memory usage of Infinitus classification
Looking at 'recursion' from the memory usage of Infinitus classification
Looking at 'recursion' from the memory usage of Infinitus classification
In PHP's infinite classification, many methods used are recursive, but our understanding of recursion is still very vague. Next, we will have an in-depth understanding of the advantages and disadvantages of recursion so that everyone can have an understanding of it. Comprehensive understanding.
What is recursion?
Definition
Recursion (English: Recursion), also translated as recursion, in mathematics and computer science, refers to the function Methods that use the function itself in the definition.
The etymological analysis of English Recursion is just "re- (again)" + "curs- (come, happen)", which means recurrence and reappearance. The corresponding Chinese translation "recursion" expresses two meanings: "recursion" + "return". These two meanings are the essence of recursive thinking. From this perspective, the Chinese translation is more expressive.
I saw this analogy again and again on the Internet:
Suppose you are in a movie theater and you want to know which row you are sitting in, but the person in front of you There are so many that you are too lazy to count, so you ask the person in the front row "Which row are you sitting in?", so that after the person in front (code name A) answers you, you will know which row you are in - as long as Add one to A's answer to determine your row. Unexpectedly, A is lazier than you, and he doesn’t want to count, so he also asks the person in front of him, B, “Which row are you sitting in?”, so that A can use the same steps as you to know which row he is in. Then B does the same thing. Until the group of people asked about the front row, the person in the first row told the person who asked the question "I am in the first row." Finally everyone knows which row they are in. 
The difference between a loop
Just look at the definition in the wiki above, It seems to be very similar to what is usually called an infinite loop. What is the difference between them?
Recursion is movement in silence, going and returning.
The cycle is the same movement and stillness, and there is no return.
For example, you are given a key. You stand in front of the door and ask how many doors you can open with this key.
Recursion: You open the door in front of you and see another door in the house (this door may be the same size as the door opened in front (quiet), or it may be smaller (moving)), you Walking over, you find that the key in your hand can still open it. You push the door open and find that there is another door inside. You continue to open it. . . , after several times, you open a door in front of you and find that there is only one room and no door. You start walking back the same way, and every time you walk back to a room, you count once. When you reach the entrance, you can answer how many doors you opened with this key.
Loop: You open the door in front of you and see another door in the house, (this door may be the same size as the door opened in front (quiet), or it may be smaller (moving)), You walk over and find that the key in your hand can still open it. You push the door open and find that there is another door inside. (If the previous door is the same, this door is the same. If the second door is smaller than the first door, , this door is also smaller than the second door (the movement is the same, either no change, or the same change)), you continue to open this door. . . , keep going like this. The person at the entrance never waits for you to come back and tell him the answer.
Recursive Thought
Recursion means going (going) and coming back (returning).
Specifically, why can we "go"?
This problem that requires recursion needs to be able to use the same problem-solving ideas to answer similar but slightly different questions (the key in the above example can open the lock on the back door).
Why can there be "return"?
This requires that in the process of these problems constantly moving from big to small, from near to far, there will be an end point, a critical point, a baseline, and when you reach that point, you no longer need to go to smaller or farther places. Go down to the starting point, and then start from that point and return to the original point.
The basic idea of recursion is to transform large-scale problems into small-scale similar sub-problems to solve. When implementing a function, because the method of solving big problems and the method of solving small problems are often the same, the function calls itself. In addition, the function that solves the problem must have an obvious end condition, so that infinite recursion will not occur.
When do you need to use recursion?
#When the definition of some problems itself is in recursive form, it is most suitable to use recursion to solve it.
Students majoring in computer science are most familiar with the definition of "tree" [4,5]. There are also some definitions, such as factorial, Fibonacci sequence [6], etc. Using recursion to solve these problems often solves some seemingly "scary" problems in just a few lines of code. Of course, recursive performance issues are another matter. Stack allocation and function call costs must be considered in specific engineering practices. But if we are just discussing recursive thoughts now, we might as well put those aside and appreciate the beauty of recursion.
Recursion simplifies the way we think when solving certain problems, and the code is more refined and easier to read. So since recursion has so many advantages, should we use recursion to solve all problems? Does recursion have no disadvantages? Today we will discuss the shortcomings of recursion. When it comes to recursion, we have to face its efficiency problem.
Why is recursion inefficient?
Let’s take the Fibonacci sequence as an example. In many textbooks or articles where recursion or computational complexity is mentioned, the program for calculating the Fibonacci sequence is used as a classic example. If you are now asked to write a function that calculates the nth number of the Fibonacci sequence in C# as quickly as possible (regardless of exceptions such as parameters less than 1 or result overflow), I don’t know if your program will match the following code Similar:
public static ulong Fib(ulong n)
{
return (n == 1 || n == 2) ? 1 : Fib(n - 1) + Fib(n - 2);
}This code should be considered short and concise (the execution code is only one line), intuitive and clear, and very consistent with the code aesthetics of many programmers. Many people may have this in mind when writing such code during interviews. It will also feel good secretly. But if you use this code to try to calculate Fib(1000), I think you won't be happy anymore. Its running time may make you crazy.
It seems that good-looking code may not be useful. If the efficiency of the program cannot be accepted, then all the good-looking code will be in vain. If you briefly analyze the execution flow of the program, you will find the problem. Taking the calculation of Fibonacci(5) as an example:
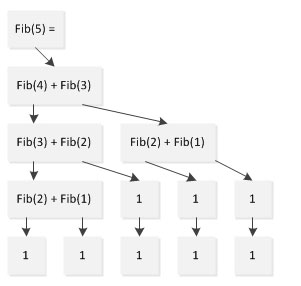
As can be seen from the above figure, when calculating Fib In the process of (5), Fib(1) was calculated twice, Fib(2) was calculated three times, and Fib(3) was calculated twice. The task that originally only required 5 calculations was calculated 9 times. . This problem will become more and more prominent as the scale increases, so that Fib(1000) can no longer be calculated in an acceptable time.
What we used at that time was to simply use the definition to find fib(n), that is, use the formula fib(n) = fib(n-1) + fib(n-2). It is easy to think of this idea, but after careful analysis we find that when fib(n-1) is called, fib(n-2) is also called, which means that fib(n-2) is called twice. , by the same token, f(n-3) is also called twice when f(n-2) is called, and these redundant calls are completely unnecessary. It can be calculated that the complexity of this algorithm is exponential.
Improved Fibonacci recursive algorithm
So is there a better recursive algorithm for calculating the Fibonacci sequence? Of course there is. Let’s take a look at the first few Fibonacci numbers:
11, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Did you notice? , if we remove the previous item, the resulting sequence still satisfies f(n) = f(n-1) – f(n-2), (n>2), and the sequence we obtain starts with 1, 2 . It is easy to find that the n-1th item of this sequence is the nth item of the original sequence. How about it, do you know how we should design the algorithm? We can write such a function, which accepts three parameters, the first two are the first two items of the sequence, and the third is the number of the sequence that we want to find starting with the first two parameters.
1int fib_i(int a, int b, int n);
Inside the function we first check the value of n. If n is 3, we only need to return a+b, This is a simple situation. If n>3, then we call f(b, a+b, n-1), which reduces the size of the problem (from finding the nth term to finding the n-1th term). Okay, the final code is as follows:
int fib_i(int a, int b , int n)
{
if(n == 3)
return a+b;
else
return fib_i(b, a+b, n-1);
}Why is there a large overhead on memory?
The principle of recursion is: first store the variable value to be calculated on the stack, and then loop in sequence until the recursion end condition is met, then take the variable value to be calculated from the stack and calculate the final result.
An analogy: Calculate 10! =
For recursion, the process is: 10! = 10*9!
9! = 9*8!
...
2! =2*1!
1! =1
When calculating, it stores expressions into memory one by one until the recursive condition satisfies 1! =1, and then retrieve the expression just saved from the memory to get the final result. In this case, more system resources will be spent.
And the system will set the maximum recursion depth. If it is greater than this depth, an error will be reported and exited. During the recursive calling of a function, the parameters, return values, etc. in the function will be continuously pushed onto the stack. Function calls will constantly use the stack, report and restore the scene, so the memory overhead will become larger and larger. The solution is tail recursion. However, PHP has no optimization effect on tail recursion, so this solution is not practical. significance.

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1393
1393
 52
52
 37
37
 110
110
 How to fine-tune deepseek locally
Feb 19, 2025 pm 05:21 PM
How to fine-tune deepseek locally
Feb 19, 2025 pm 05:21 PM
Local fine-tuning of DeepSeek class models faces the challenge of insufficient computing resources and expertise. To address these challenges, the following strategies can be adopted: Model quantization: convert model parameters into low-precision integers, reducing memory footprint. Use smaller models: Select a pretrained model with smaller parameters for easier local fine-tuning. Data selection and preprocessing: Select high-quality data and perform appropriate preprocessing to avoid poor data quality affecting model effectiveness. Batch training: For large data sets, load data in batches for training to avoid memory overflow. Acceleration with GPU: Use independent graphics cards to accelerate the training process and shorten the training time.
 For only $250, Hugging Face's technical director teaches you how to fine-tune Llama 3 step by step
May 06, 2024 pm 03:52 PM
For only $250, Hugging Face's technical director teaches you how to fine-tune Llama 3 step by step
May 06, 2024 pm 03:52 PM
The familiar open source large language models such as Llama3 launched by Meta, Mistral and Mixtral models launched by MistralAI, and Jamba launched by AI21 Lab have become competitors of OpenAI. In most cases, users need to fine-tune these open source models based on their own data to fully unleash the model's potential. It is not difficult to fine-tune a large language model (such as Mistral) compared to a small one using Q-Learning on a single GPU, but efficient fine-tuning of a large model like Llama370b or Mixtral has remained a challenge until now. Therefore, Philipp Sch, technical director of HuggingFace
 What to do if the Edge browser takes up too much memory What to do if the Edge browser takes up too much memory
May 09, 2024 am 11:10 AM
What to do if the Edge browser takes up too much memory What to do if the Edge browser takes up too much memory
May 09, 2024 am 11:10 AM
1. First, enter the Edge browser and click the three dots in the upper right corner. 2. Then, select [Extensions] in the taskbar. 3. Next, close or uninstall the plug-ins you do not need.
 The impact of the AI wave is obvious. TrendForce has revised up its forecast for DRAM memory and NAND flash memory contract price increases this quarter.
May 07, 2024 pm 09:58 PM
The impact of the AI wave is obvious. TrendForce has revised up its forecast for DRAM memory and NAND flash memory contract price increases this quarter.
May 07, 2024 pm 09:58 PM
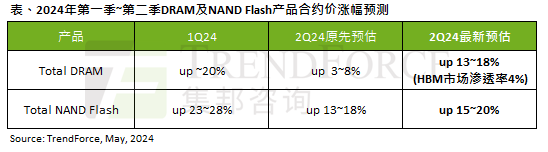
According to a TrendForce survey report, the AI wave has a significant impact on the DRAM memory and NAND flash memory markets. In this site’s news on May 7, TrendForce said in its latest research report today that the agency has increased the contract price increases for two types of storage products this quarter. Specifically, TrendForce originally estimated that the DRAM memory contract price in the second quarter of 2024 will increase by 3~8%, and now estimates it at 13~18%; in terms of NAND flash memory, the original estimate will increase by 13~18%, and the new estimate is 15%. ~20%, only eMMC/UFS has a lower increase of 10%. ▲Image source TrendForce TrendForce stated that the agency originally expected to continue to
 A beginner's guide to C++ recursion: Building foundations and developing intuition
May 01, 2024 pm 05:36 PM
A beginner's guide to C++ recursion: Building foundations and developing intuition
May 01, 2024 pm 05:36 PM
Recursion is a powerful technique that allows a function to call itself to solve a problem. In C++, a recursive function consists of two key elements: the base case (which determines when the recursion stops) and the recursive call (which breaks the problem into smaller sub-problems ). By understanding the basics and practicing practical examples such as factorial calculations, Fibonacci sequences, and binary tree traversals, you can build your recursive intuition and use it in your code with confidence.
 Detailed explanation of C++ function recursion: tail recursion optimization
May 03, 2024 pm 04:42 PM
Detailed explanation of C++ function recursion: tail recursion optimization
May 03, 2024 pm 04:42 PM
Recursive definition and optimization: Recursive: A function calls itself internally to solve difficult problems that can be decomposed into smaller sub-problems. Tail recursion: The function performs all calculations before making a recursive call, which can be optimized into a loop. Tail recursion optimization condition: recursive call is the last operation. The recursive call parameters are the same as the original call parameters. Practical example: Calculate factorial: The auxiliary function factorial_helper implements tail recursion optimization, eliminates the call stack, and improves efficiency. Calculate Fibonacci numbers: The tail recursive function fibonacci_helper uses optimization to efficiently calculate Fibonacci numbers.
 What warnings or caveats should be included in Golang function documentation?
May 04, 2024 am 11:39 AM
What warnings or caveats should be included in Golang function documentation?
May 04, 2024 am 11:39 AM
Go function documentation contains warnings and caveats that are essential for understanding potential problems and avoiding errors. These include: Parameter validation warning: Check parameter validity. Concurrency safety considerations: Indicate the thread safety of a function. Performance considerations: Highlight the high computational cost or memory footprint of a function. Return type annotation: Describes the error type returned by the function. Dependency Note: Lists external libraries or packages required by the function. Deprecation warning: Indicates that a function is deprecated and suggests an alternative.
 C++ function recursion explained: alternatives to recursion
May 01, 2024 pm 04:54 PM
C++ function recursion explained: alternatives to recursion
May 01, 2024 pm 04:54 PM
Recursion is a technique where a function calls itself, but has the disadvantages of stack overflow and inefficiency. Alternatives include: tail-recursion optimization, where the compiler optimizes recursive calls into loops; iteration, which uses loops instead of recursion; and coroutines, which allow execution to be paused and resumed, simulating recursive behavior.



