How to implement binary search tree in Python

BinarySearchTree (binary sorting tree) The data structure of each node is 1 parent node pointer, 1 left child pointer, 1 child pointer, and itself The data part of are all larger than the node.

Binary Search Tree

We already know two different ways to obtain key-value pairs in a collection. Recall how these collections implement ADTs (Abstract Data Types) MAP. We discuss two implementations of ADT MAP, list-based binary search and hash table. In this section, we are going to learn about binary search trees, which are another Map collection whose keys point to values. In this case, we do not need to consider the actual position of the element in the tree, but we need to know that binary trees are used to search for more information. Efficient.

Search tree operation

Before we study this implementation, let us review the

interface

provided by ADT MAP. We will notice that this interface is very similar to Python's dictionary.

Map() creates a new empty Map collection.
put(
2. key

   ,val) adds a new key-value pair to the Map. If the key is already in the Map, the new value is used to replace the old value.

get(key) Provide a key and return the data saved in the Map, or return None.
del Use the del map[key] statement to
4. delete

   key-value pairs from the Map.

len() returns the number of key-value pairs saved in the Map
in If the given key is in the Map, use key in The map statement returns True.

Search tree implementation

A binary search tree, if the key values ​​in the left subtree are less than the parent node, The key values ​​in the right subtree are greater than the

attribute

of the parent node. We call this tree a BST search tree. As mentioned before, when we implement Map, the BST method will guide us to achieve this. Figure 1 illustrates this property of a binary search tree, showing keys that have no associated values. Note that this property applies to every parent node and child node. All keys in the left subtree are smaller than the key in the root node, and all keys in the right subtree are greater than the key in the root node.

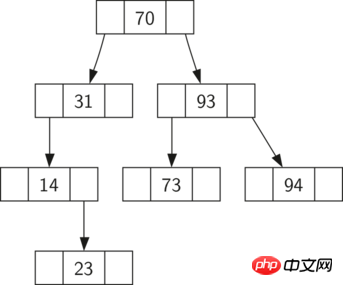Figure 1: A simple binary search tree

Now that you know what a binary search tree is, let’s look at how to construct a binary search tree Search tree, we insert these key values ​​in the search tree in the order of the nodes shown in Figure 1. The nodes in the search tree in Figure 1 are: 70, 31, 93, 94, 14, 23, 73. Because 70 is the first value inserted into the tree, it is the root node. Next, 31 is less than 70 and therefore the left subtree of 70. Next, 93 is greater than 70 and therefore the right subtree of 70. We have now filled two levels of the tree, so the next key value will be either the left or right subtree of 31 or 93. Since 94 is greater than 70 and 93, it becomes the right subtree of 93. Likewise, 14 is smaller than 70 and 31, so it becomes the left subtree of 31. 23 is also less than 31, so it must be the left subtree of 31. However, it is greater than 14, so it is the right subtree of 14.

To implement a binary search tree, we will use nodes and

references

, which is similar to the process we use to implement linked lists and expression trees. Since we must be able to create and use an empty binary search tree, we will do so using two classes, the first class we will call BinarySearchTree and the second class we will call TreeNode. The BinarySearchTree class has a reference to the TreeNode class as the root of the binary search tree. In most cases, the external class defines 's external method which simply checks if the tree is empty and if there is a node in the tree, the requirement The BinarySearchTree class contains private methods that define the root as a parameter. In this case, if the tree is empty or we want to delete the root of the tree, we have to use special operations. The code of the constructor and some other functions of the BinarySearchTree class is shown in Listing 1. Listing 1

class BinarySearchTree:

  def init(self):
    self.root = None
    self.size = 0

  def length(self):
    return self.size

  def len(self):
    return self.size

  def iter(self):
    return self.root.iter()

The TreeNode class provides many auxiliary functions to make the implementation of the methods of the BinarySearchTree class easier. As shown in Listing 2, the structure of a tree node is implemented by these auxiliary functions. As you can see, these helper functions can divide a node as a left or right child based on its position and the type of that child. The TreeNode class tracks the properties of each parent node very clearly. You'll see why this is important when we discuss the implementation of the delete operation.

Another interesting thing about the TreeNode implementation in Listing 2 is that we use Python’s optional parameters. The optional parameters easily allow us to create a tree node in several different situations. Sometimes we want to create a new tree node even if we already have a parent and child node. Like the existing parent and child nodes, we can pass the parent and child nodes as parameters. Sometimes we also create a tree containing key-value pairs and we don't pass any parameters for parent or child nodes. In this case we will use the default values ​​of the optional parameters.

Listing 2

class TreeNode:
  def init(self,key,val,left=None,right=None,
                    parent=None):
    self.key = key
    self.payload = val
    self.leftChild = left
    self.rightChild = right
    self.parent = parent

  def hasLeftChild(self):
    return self.leftChild

  def hasRightChild(self):
    return self.rightChild

  def isLeftChild(self):
    return self.parent and self.parent.leftChild == self

  def isRightChild(self):
    return self.parent and self.parent.rightChild == self

  def isRoot(self):
    return not self.parent

  def isLeaf(self):
    return not (self.rightChild or self.leftChild)

  def hasAnyChildren(self):
    return self.rightChild or self.leftChild

  def hasBothChildren(self):
    return self.rightChild and self.leftChild

  def replaceNodeData(self,key,value,lc,rc):
    self.key = key
    self.payload = value
    self.leftChild = lc
    self.rightChild = rc
    if self.hasLeftChild():
      self.leftChild.parent = self
    if self.hasRightChild():
      self.rightChild.parent = self

Now that we have the BinarySearchTree and TreeNode classes, it’s time to write a put method that allows us to build a binary search tree. The put method is a method of BinarySearchTree class. This method will check if the tree is already rooted. If not, we will create a new tree node and set it as the root of the tree. If there is already a root node, we call it itself, perform recursion, and use the auxiliary function _put to search the tree according to the following algorithm:

Start from the root node of the tree and search the binary tree To compare the new key value with the key value of the current node, if the new key value is less than the current node, search the left subtree. If the new key is greater than the current node, the right subtree is searched.

When the left (or right) subtree cannot be searched, our position in the tree is where the new node is set.
Add a node to the tree, create a new TreeNode object and insert this object in the previous node at this point.

Listing 3 shows the Python code to insert a new node in the tree. The _put function should follow the above steps to write a recursive algorithm. Note that when a new subtree is inserted, the current node (CurrentNode) is passed to the new tree as the parent node.

An important problem when we perform insertion is that duplicate key values ​​cannot be processed correctly. Our tree implements key value replication, which will create a new node in the right subtree with the same key value as the original node. node. The consequence of this is that new nodes will not be discovered during the search. We use a better way to handle inserting duplicate key values, where the old value is replaced by the value associated with the new key. We leave the fix for this bug as Exercise to you.

Listing 3

def put(self,key,val):
  if self.root:
    self._put(key,val,self.root)
  else:
    self.root = TreeNode(key,val)
  self.size = self.size + 1

def _put(self,key,val,currentNode):
  if key < currentNode.key:
    if currentNode.hasLeftChild():
        self._put(key,val,currentNode.leftChild)
    else:
        currentNode.leftChild = TreeNode(key,val,parent=currentNode)
  else:
    if currentNode.hasRightChild():
        self._put(key,val,currentNode.rightChild)
    else:
        currentNode.rightChild = TreeNode(key,val,parent=currentNode)

With the implementation of the put method, we can easily reset it through the setitem method Load [] as operator to call the put method (see Listing 4). This allows us to write python statements like myZipTree['Plymouth'] = 55446, which looks just like a Python dictionary.

Listing 4

##

def setitem(self,k,v):
  self.put(k,v)

Figure 2 illustrates the process of inserting a new node into a binary search tree. The gray nodes show the order of tree nodes traversed during the insertion process.

Figure 2: Inserting a node with key value = 19

Once the tree is constructed, the next task is to implement it for a given key value Retrieve. The get method is easier than the put method because it simply searches the tree recursively until either a mismatching leaf node is found or a matching key value is found. When a matching key value is found, the value in the node is returned.

Listing 5 shows the code for get, _get and getitem. The code searched with the _get method has the same logic of selecting the left or right subtree as the put method. Please note that the _get method returns the value of get in TreeNode. _get can be used as a flexible and effective way to provide parameters for other methods of BinarySearchTree that may need to use data in TreeNode.

By implementing the getitem method, we can write a Python statement that looks like we are accessing a dictionary, when in fact we are just operating a binary search tree, such as Z = myziptree['fargo']. As you can see, the getitem method is calling get.

Listing 5

def get(self,key):
  if self.root:
    res = self._get(key,self.root)
    if res:
        return res.payload
    else:
        return None
  else:
    return None

def _get(self,key,currentNode):
  if not currentNode:
    return None
  elif currentNode.key == key:
    return currentNode
  elif key < currentNode.key:
    return self._get(key,currentNode.leftChild)
  else:
    return self._get(key,currentNode.rightChild)

def getitem(self,key):
  return self.get(key)

使用get，我们可以通过写一个BinarySearchTree的contains方法来实现操作，contains方法简单地调用了get方法，如果它有返回值就返回True，如果它是None就返回False。如Listing 6 所示。

Listing 6

def contains(self,key):
  if self._get(key,self.root):
    return True
  else:
    return False

回顾一下contains重载的操作符，这允许我们写这样的语句：

if 'Northfield' in myZipTree:
  print("oom ya ya")

The above is the detailed content of How to implement binary search tree in Python. For more information, please follow other related articles on the PHP Chinese website!